darknet c++源码阅读笔记-01-activation_kernels.cu


//! __device__ 函数限定符，指定函数在设备端执行。
__device__ float lhtan_activate_kernel(float x)
{
    if(x < 0) return .001*x;
    if(x > 1) return .001*(x-1) + 1;
    return x;
}

红色的是tanh函数，绿色的是lhtan函数，值的范围是(负无穷小，正无穷大)，梯度很小，看不出来是无穷大。

2. lhtan_gradient_kernel

是lhtan_activate_kernel函数的梯度，x<0时，-0.001*x的梯度是0.001，0<=x<=1时，梯度是1.


//! lhtan_activate_kernel的梯度值
__device__ float lhtan_gradient_kernel(float x)
{
    if(x > 0 && x < 1) return 1;
    return .001;
}

3. hardtan_activate_kernel

hard tanh激活函数。


//! hard tanh激活函数
__device__ float hardtan_activate_kernel(float x)
{
    if (x < -1) return -1;
    if (x > 1) return 1;
    return x;
}

红色是tanh正切函数，黑色是hard tanh函数，绿色是hard tanh的梯度函数。

4. linear_activate_kernel

线性激活函数.

__device__ float linear_activate_kernel(float x){return x;}

5. logistic_activate_kernel

逻辑回归的激活函数，也称sigmoid激活函数，特点是将y值归一化到（0，1）之间。画图工具。

__device__ float logistic_activate_kernel(float x){return 1.f/(1.f + expf(-x));}

红色的是sigmoid函数，绿色是其倒数f(x) * (1-f(x))，可以看到x=0时，梯度值最大。

求梯度代码：

__device__ float logistic_gradient_kernel(float x){return (1-x)*x;}  // 这里的x应该是sigmoid的y值

6. loggy_activate_kernel

与上面的sigmoid函数形态类似，不同的是归一化后y范围是（-1，1）.

y = 2 / ( 1 + exp(-x) ) - 1.

参考sigmoid函数求导方法，求导y’ = 2*sigmoid(x)(1-sigmoid(x))

紫色是loggy激活函数，红色是其倒数。

__device__ float loggy_activate_kernel(float x){return 2.f/(1.f + expf(-x)) - 1;}  // 范围（-1，1）


__device__ float loggy_gradient_kernel(float x)  // x = 2 / (1+exp(-a)) - 1
{
    float y = (x+1.F)/2.F;  // y =  (2 / (1+exp(-a)) - 1 + 1) / 2 = 1 / (1+exp(-a)) = y，即sigmoid函数。
    return 2*(1-y)*y;  // 
}

7.relu_activate_kernel

常用的relu激活函数。ReLU = max(0, x)，小于0的梯度为0.

推荐一个好用的画图工具。

__device__ float relu_activate_kernel(float x){return x*(x>0);}

__device__ float relu_gradient_kernel(float x){return (x>0);}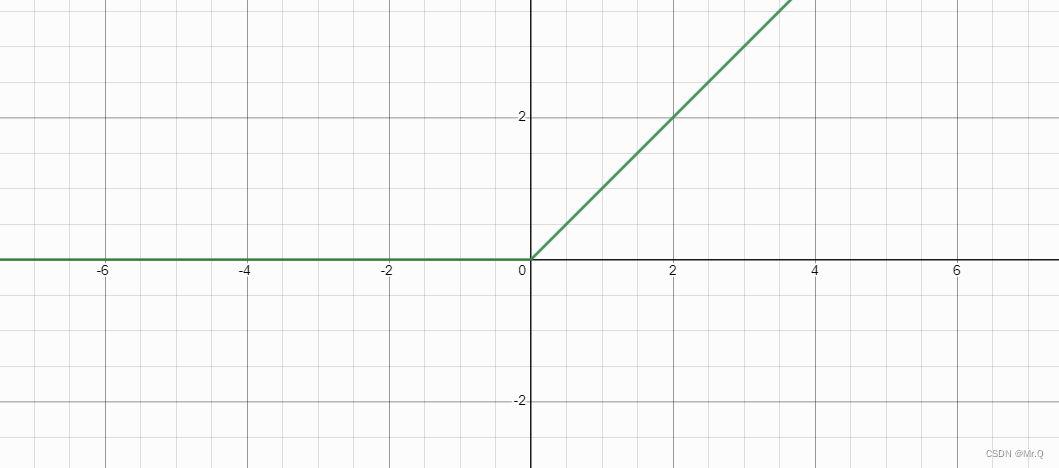

8. relu6_activate_kernel

相对于relu，不止抑制了小于0的值，也抑制了较大的值（大于6的值）。ReLU6=min(6, max(0,x))

__device__ float relu6_activate_kernel(float x) { return min_val_cmp(max_val_cmp(x, 0), 6); }

__device__ float relu6_gradient_kernel(float x) { return (x > 0 && x < 6); }

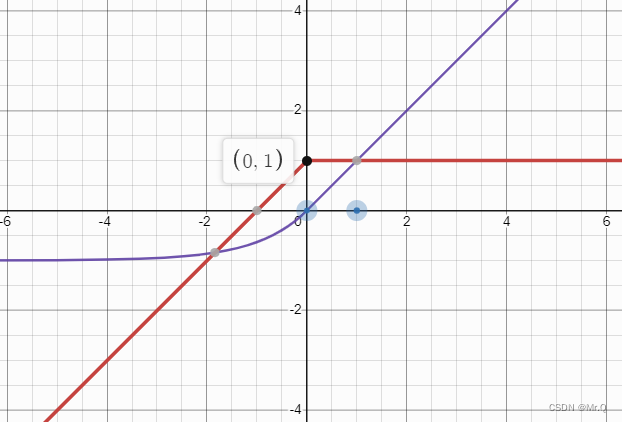
9. elu_activate_kernel

ELU相对于ReLU的特点是多了个"e"，即没有直接丢弃左边小于0的部分，而是用e^x激活。

（1）大于0的部分：(x >= 0)*x，和ReLU一样，不变；

（2）小于0的部分：(x < 0)*(expf(x)-1)，即e^x-1；

__device__ float elu_activate_kernel(float x){return (x >= 0)*x + (x < 0)*(expf(x)-1);}


//! x = e^a-1, x'=-e^a = 1+x
__device__ float elu_gradient_kernel(float x){return (x >= 0) + (x < 0)*(x + 1);} // 大于0时，梯度为1，小于0时，梯度为x+1

10. selu_activate_kernel

SELU（the scaled exponential linear units）相对于ELU多了个S，即前面加了大于1的系数。

大于0的部分系数是1.0507；小于0的部分系数是1.0507*1.6732；

__device__ float selu_activate_kernel(float x) { return (x >= 0)*1.0507f*x + (x < 0)*1.0507f*1.6732f*(expf(x) - 1); }


//! x = 1.0507*1.6732*(e^a-1), x' = x(1+b/x)=x+b
__device__ float selu_gradient_kernel(float x) { return (x >= 0)*1.0507f + (x < 0)*(x + 1.0507f*1.6732f); }

蓝色的是ELU，绿色的是SELU。

11. relie_activate_kernel

也就是leaky ReLU，相对于ReLU，保留了小于0时的梯度。

__device__ float relie_activate_kernel(float x){return (x>0) ? x : .01f*x;}  // leaky ReLU

__device__ float relie_gradient_kernel(float x){return (x>0) ? 1 : .01f;}

12. ramp_activate_kernel

ramp就是在ReLU+0.1*x

__device__ float ramp_activate_kernel(float x){return x*(x>0)+.1f*x;}  // ReLU + 0.1*x

__device__ float ramp_gradient_kernel(float x){return (x>0)+.1f;}

13. leaky_activate_kernel

相对于ReLU，保留了小于0时的梯度。

__device__ float leaky_activate_kernel(float x){return (x>0) ? x : .1f*x;}  // 和relie_activate_kernel一样。

__device__ float leaky_gradient_kernel(float x){return (x>0) ? 1 : .1f;}

14. tanh_activate_kernel

tanh激活函数。范围 (-1, 1)，相对于前面的loggy_activate_kernel：2.f/(1.f + expf(-x)) - 1，x系数变成了-2，梯度更大。

__device__ float tanh_activate_kernel(float x){return (2/(1 + expf(-2*x)) - 1);}


//! x = 2/(1+exp(-2a)) - 1, x'= (x+1)*2*(1-(x+1)/2) = (x+1)(1-x) = (1-x^2)
__device__ float tanh_gradient_kernel(float x){return 1-x*x;}

红色的是tanh激活函数，绿色的是loggy_activate_kernel，紫色是tanh函数的梯度函数。

15. gelu_activate_kernel

GELU相对于ReLU，越大梯度值越接近1，越小越接近0，没有直接置为0. 范围是（0,无穷大]，

__device__ float gelu_activate_kernel(float x){return (0.5*x*(1 + tanhf(0.797885*x + 0.035677*powf(x, 3))));}


__device__ float gelu_gradient_kernel(float x) {
    const float x3 = powf(x, 3);
    return 0.5*tanhf(0.0356774*x3 + 0.797885*x) + (0.0535161*x3 + 0.398942*x) * powf(sech_gpu(0.0356774*x3 + 0.797885*x), 2) + 0.5;
}

16. softplus_kernel

softplus(x) = ln(1+exp(x))，范围（0，无穷大）具体实现如下。

（1）太大的，直接返回；

（2）太小的，返回e^x；

（3）中间的，返回ln(1+exp(x)).


__device__ float softplus_kernel(float x, float threshold = 20) {
    if (x > threshold) return x;                // too large
    else if (x < -threshold) return expf(x);    // too small
    return log1pf(expf(x));  // log1pf(val)返回ln(val+1)
    //return logf(expf(x) + 1);
}

17. plse_activate_kernel

分段线性激活。


__device__ float plse_activate_kernel(float x)
{
    if(x < -4) return .01f * (x + 4);
    if(x > 4)  return .01f * (x - 4) + 1;
    return .125f*x + .5f;
}

18. sech_gpu

__device__ float sech_gpu(float x) { return 2 / (expf(x) + expf(-x)); }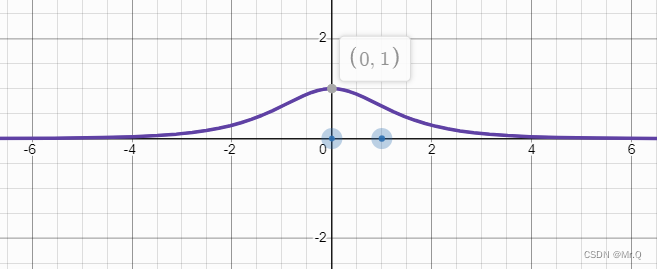

19. activate_kernel

使用上面定义的激活函数。


/***
* 根据传入的枚举类型，返回的激活值
typedef enum {
LOGISTIC, RELU, RELU6, RELIE, LINEAR, RAMP, TANH, PLSE, REVLEAKY, LEAKY, ELU, LOGGY, STAIR, HARDTAN, LHTAN, SELU, GELU, SWISH, MISH, HARD_MISH, NORM_CHAN, NORM_CHAN_SOFTMAX, NORM_CHAN_SOFTMAX_MAXVAL
}ACTIVATION;
***/
__device__ float activate_kernel(float x, ACTIVATION a)
{
    switch(a){
        case LINEAR:
            return linear_activate_kernel(x);
        case LOGISTIC:
            return logistic_activate_kernel(x);
        case LOGGY:
            return loggy_activate_kernel(x);
        case RELU:
            return relu_activate_kernel(x);
        case RELU6:
            return relu6_activate_kernel(x);
        case ELU:
            return elu_activate_kernel(x);
        case SELU:
            return selu_activate_kernel(x);
        case GELU:
            return gelu_activate_kernel(x);
        case RELIE:
            return relie_activate_kernel(x);
        case RAMP:
            return ramp_activate_kernel(x);
        case LEAKY:
            return leaky_activate_kernel(x);
        case TANH:
            return tanh_activate_kernel(x);
        case PLSE:
            return plse_activate_kernel(x);
        case STAIR:
            return stair_activate_kernel(x);
        case HARDTAN:
            return hardtan_activate_kernel(x);
        case LHTAN:
            return lhtan_activate_kernel(x);
    }
    return 0;
}

20. gradient_kernel


/***
根据不同的激活函数，调用对应的梯度函数
***/
__device__ float gradient_kernel(float x, ACTIVATION a)
{
    switch (a) {
    case LINEAR:
        return linear_gradient_kernel(x);
    case LOGISTIC:
        return logistic_gradient_kernel(x);
    case LOGGY:
        return loggy_gradient_kernel(x);
    case RELU:
        return relu_gradient_kernel(x);
    case RELU6:
        return relu6_gradient_kernel(x);
    case NORM_CHAN:
        return relu_gradient_kernel(x);
    case ELU:
        return elu_gradient_kernel(x);
    case SELU:
        return selu_gradient_kernel(x);
    case GELU:
        return gelu_gradient_kernel(x);
    case RELIE:
        return relie_gradient_kernel(x);
    case RAMP:
        return ramp_gradient_kernel(x);
    case LEAKY:
        return leaky_gradient_kernel(x);
    case TANH:
        return tanh_gradient_kernel(x);
    case PLSE:
        return plse_gradient_kernel(x);
    case STAIR:
        return stair_gradient_kernel(x);
    case HARDTAN:
        return hardtan_gradient_kernel(x);
    case LHTAN:
        return lhtan_gradient_kernel(x);
    }
    return 0;
}

参考源码：https://github.com/pjreddie/darknet

相关阅读:
如何快速本地搭建悟空CRM结合内网穿透工具高效远程办公
 paddlespeech 语音识别 web流服务部署(Streaming Speech Recognition)
基于springboot实现医院信管系统项目【项目源码+论文说明】
HTTP请求偶尔失败（21秒后超时） - 问题排查
 Bpmn在vue中不能使用require 进行导入图片，而是要使用new URL
java合成多个pdf为一个pdf
adb pull 使用
 mysql死锁排查及解决
 支持向量机核技巧：10个常用的核函数总结
 【Web开发】CSS教学(超详细,满满的干货)
原文地址：https://blog.csdn.net/jizhidexiaoming/article/details/125997437