此处提供一个红黑树在线生成网站：Red/Black Tree Visualization

一、简介

红黑树的引入

有了二叉搜索树，为什么还需要平衡二叉树?

• 二叉树容易退化成一条链
• 此时查询的时间复杂度也由O(log₂N)将退化成O(N)
• 而平衡二叉树对左右子树高度差有限制，保证最坏的时间复杂度为O(log₂N)

有了平衡二叉树，为什么还要红黑树？

• AVL的左右子树高度差不能超过1，每次进行插入/删除操作时，几乎都需要通过旋转操作保持平衡
• 在频繁进行插入/删除的场景中，频繁的旋转操作使得AVL的性能大打折扣
• 红黑树通过牺牲严格的平衡，换取插入/删除时少量的旋转操作，整体性能优于AVL
• 红黑树插入时的不平衡，不超过两次旋转就可以解决；删除时的不平衡，不超过三次旋转就能解决
• 红黑树的红黑规则，保证最坏的情况下，也能在O(log₂N)时间内完成查找操作。

红黑树简介

红黑树是一种自平衡的二叉查找树，是一种高效的查找树。它是由 Rudolf Bayer 于1978年发明，在当时被称为平衡二叉 B 树(symmetric binary B-trees)。后来，在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改为如今的红黑树。红黑树具有良好的效率，它可在O(logN)时间内完成查找、增加、删除等操作。

红黑树特性

红黑树保证最长路径步长最短路径的两倍，因而近似平衡（最短路径就是全黑色节点，最长路径就是一个红色节点一个黑色节点，当从根节点到叶子节点的路径上黑色节点相同时，最长路径刚好是最短路径的两倍）。红黑树最高高度不超过 2 * log₂(n+1)

5大特性：

1. 节点要么是黑色要么是红色
2. 根节点是黑色
3. 叶子节点（外部节点，空节点）都是黑色[最底层的NIL]。
4. 红色节点的子节点都是黑色
5. 从任意节点到叶子节点的所有路径都包含相同数目的黑色节点

引申问题

①从根节点到叶子节点的最长路径不大于最短路径的 2 倍

怎么样的路径算最短路径?从规则 5 中，我们知道从根节点到每个叶子节点的黑色节点数量是一样的，那么纯由黑色节点组成的路径就是最短路径。

什么样的路径算是最长路径?根据规则 4 和规则 3，若有红色节点，则必然有一个连接的黑色节点，当红色节点和黑色节点数量相同时，就是最长路径，也就是黑色节点(或红色节点)*2。

②为什么说新加入到红黑树中的节点为红色节点

从规则 4 中知道，当前红黑树中从根节点到每个叶子节点的黑色节点数量是一样的，此时假如新的是黑色节点的话，必然破坏规则。

但加入红色节点却不一定，除非其父节点就是红色节点，因此加入红色节点，破坏规则的可能性小一些，下面我们也会举例来说明。

什么情况下，红黑树的结构会被破坏呢?破坏后又怎么维持平衡，维持平衡主要通过两种方式【变色】和【旋转】，【旋转】又分【左旋】和【右旋】，两种方式可相互结合。

二、左旋与右旋

左旋： 以某个结点作为支点(旋转结点)，其右子结点变为旋转结点的父结点，右子结点的左子结点变为旋转结点的右子结点，左子结点保持不变

右旋： 以某个结点作为支点(旋转结点)，其左子结点变为旋转结点的父结点，左子结点的右子结点变为旋转结点的左子结点，右子结点保持不变

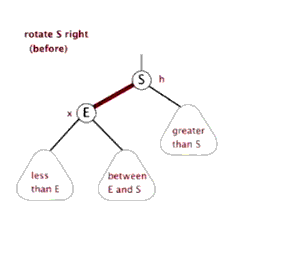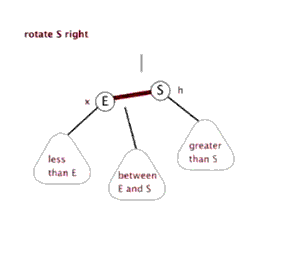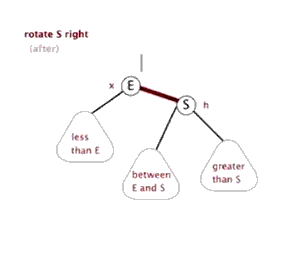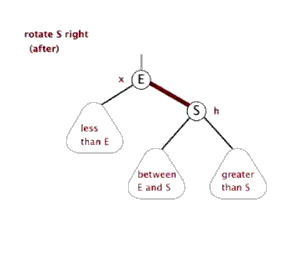
三、红黑树节点插入

插入步骤

1. 将红黑树当作一颗二叉查找树，将节点插入。
2. 将插入的节点着色为"红色"。
3. 通过一系列的旋转或着色等操作，使之重新成为一颗红黑树。

三种插入情况

根据被插入节点的父节点的情况，可以将"当节点z被着色为红色节点，并插入二叉树"划分为三种情况来处理。

1. 被插入的节点是根节点。
   直接把此节点涂为黑色。
2. 被插入的节点的父节点是黑色。
   什么也不需要做。节点被插入后，仍然是红黑树。
3. 被插入的节点的父节点是红色。
   那么，该情况与红黑树的“特性(5)”相冲突。这种情况下，被插入节点是一定存在非空祖父节点的；进一步的讲，被插入节点也一定存在叔叔节点(即使叔叔节点为空，我们也视之为存在，空节点本身就是黑色节点)。理解这点之后，我们依据"叔叔节点的情况"，将这种情况进一步划分为2种情况(Case)。

Case 1

当前节点的父节点是红色，且当前节点的祖父节点的另一个子节点（叔叔节点）也是红色。

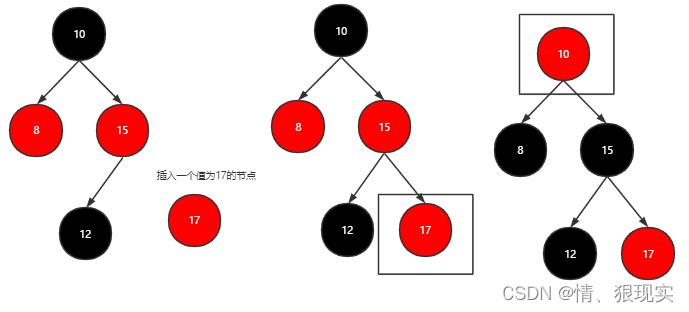
(01) 将“父节点”设为黑色。
(02) 将“叔叔节点”设为黑色。
(03) 将“祖父节点”设为“红色”。
(04) 将“祖父节点”设为“当前节点”(红色节点)；即，之后继续对“当前节点”进行操作。

Case 2

当前节点的父节点是红色，叔叔节点是黑色，且当前节点是其父节点的右孩子或左孩子

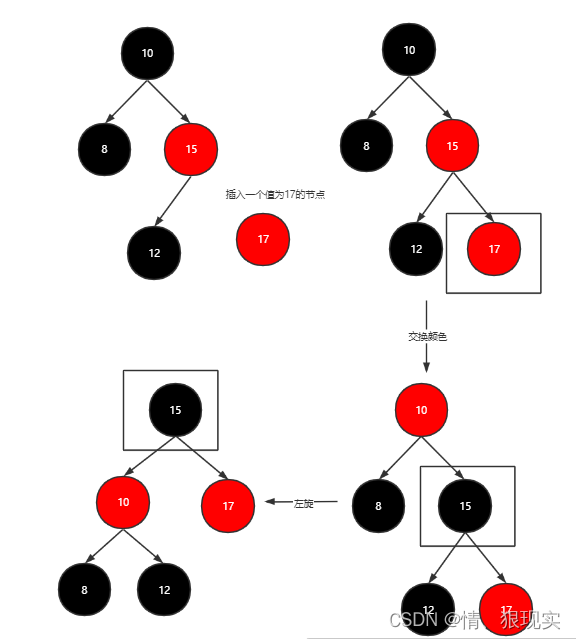
(01) 将“父节点”设为“黑色”。
(02) 将“祖父节点”设为“红色”。
(03) 以“祖父节点”为支点进行左旋或右旋。

删除节点

节点名称规定：

1. 删除节点为D
2. D的父亲节点为P
3. D的兄弟节点为B
4. D的侄子节点为N
5. D的左侄子节点为LN
6. D的右侄子节点为RN
7. D的左孩子为LC
8. D的右孩子为RC

1. 由红黑树的5个性质，当下面一层为叶子节点时，可以得出两层的红黑树的结构只能是一下5种。
   

2. 删除节点时，根据节点的位置，分为4种情况。
   情况1：删除节点为叶子节点。
   情况2：删除节点只有左孩子，没有右孩子。
   情况3：删除节点只有右孩子，没有左孩子。
   情况4：删除节点既有左孩子，又有右孩子。

情况1：删除节点为叶子节点。

1.1 如果删除叶子节点D为红色节点。操作：直接删除节点D。

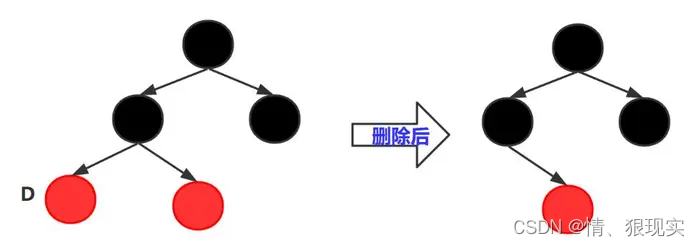
1.2 如果删除叶子节点D为黑色节点。

当节点D的兄弟节点B为黑色时，P为红色或者黑色都可以，这里P用白色圆圈表示，虚线方框内有4种情况(1)(2)(3)(4)。当节点D的兄弟节点B为红色时，P为黑色，虚线方框内只有一种情况(5)。下面讨论的是要删除的叶子结点D为节点P的左孩子。要删除的叶子结点D为节点P的右孩子，和是左孩子的分析是一样的，是对称的。这里不再重复描述。

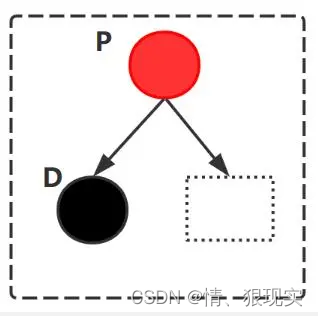
假设左边黑色节点为要删除的叶子结点D，则一共有5种情况。如下图所示。因为左边支路上有一个黑色节点。所以右边支路上也要有一个黑色节点。

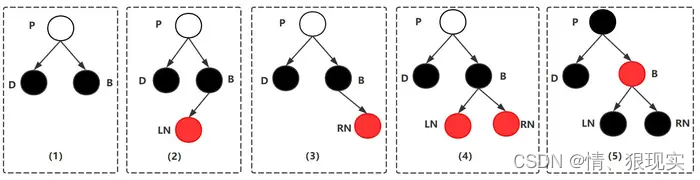
1.2.1 要删除的叶子结点D为黑色，D的兄弟节点B也为黑色。没有侄子节点。

操作：
1）先将D节点删除。
2）将P节点变成黑色，将B节点变成红色。

1.2.2 要删除的叶子结点D为黑色，D的兄弟节点B也为黑色。D的左侄子为红色。

操作：
1）先将D节点删除。
2）再将B——LN进行右旋。
3）然后将LN变成P的颜色，P节点变成黑色。
4）将P——LN——B，进行左旋。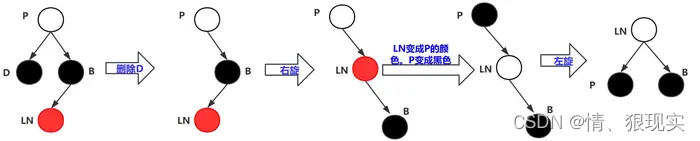

1.2.3 要删除的叶子结点D为黑色，D的兄弟节点B也为黑色。D的右侄子为红色。

操作：
1）先将D节点删除。
2）B变成P的颜色。P和RN变成黑色。
3）将P——B——RN进行左旋操作。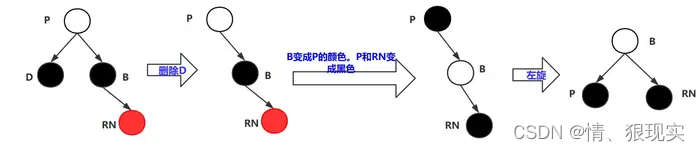

1.2.4 要删除的叶子结点D为黑色，D的兄弟节点B也为黑色。D的左侄子和右侄子都为红色。

操作：
1）先将D节点删除。
2）将P——B——RN进行左旋操作。
3）将B变成P的颜色，P和RN变成黑色。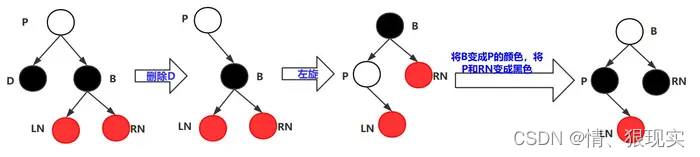

1.2.5 要删除的叶子结点D为黑色，D的兄弟节点B为红色。D的左侄子和右侄子都为黑色。

操作：
1）先将D节点删除。
2）将P——B——RN左旋
3）将B变成黑色，LN变成红色。

情况2：删除节点只有左孩子，没有右孩子。只能是如下图所示。

操作：
1）将D的值变成LC的值，
2）删除LC节点。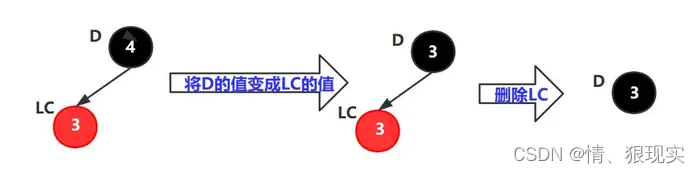

情况3：删除节点D只有右孩子，没有左孩子。

操作：
1）将D的值变成LC的值。
2）删除LC节点。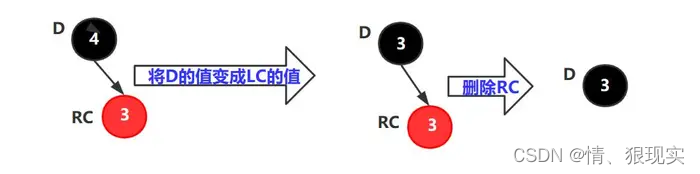

情况4：删除节点D既有左孩子，又有右孩子。

操作：
1）将D节点的值替换成D节点前驱节点的值
2）然后删除前驱节点。此时可以转换成前3种情况。

总结：

1. 如果删除节点D有左右孩子，将删除节点的值替换为删除节点前驱节点的值，然后再删除前驱结点。删除前驱结点的操作更简单。

2. 如果删除节点D只有左孩子LC，没有右孩子。将D的值替换成LC的值，然后将LC删除。

3. 如果删除节点D只有右孩子RC，没有左孩子。将D的值替换成RC的值，然后将RC删除。

4. 如果删除节点D是叶子结点，且为红色。直接删除。

5. 如果删除节点D是叶子节点，为黑色。

   1）如果兄弟节点B为黑色，也为叶子结点。删除节点D，父亲节点P变成黑色，B节点变成红色。

   2）如果兄弟节点B为黑色，不为叶子结点，如下图，有（1），（2），（3）种情况。删除节点D，然后进行旋转。旋转后前三个节点的颜色和旋转前 前三个节点对应的颜色相同。删除后如果有第四个节点，第四个节点为红色。（这是自己总结的，可能不对）

   

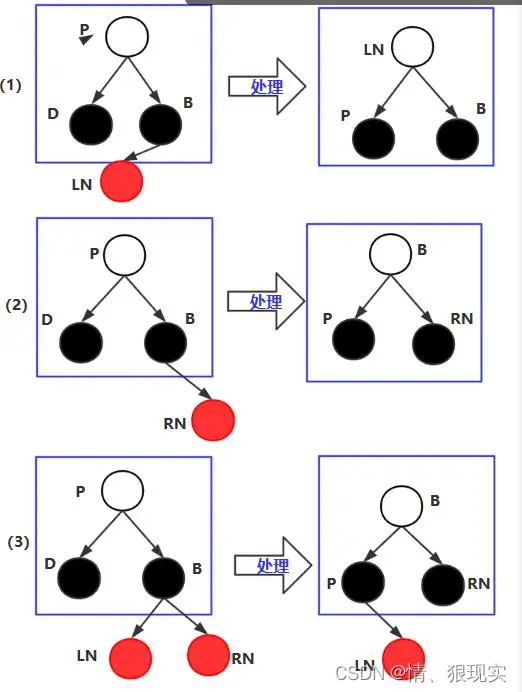
   3）如果兄弟节点为红色，则删除节点D，然后进行旋转操作。最后，前三个节点为黑色，最后一个节点为红色。