【数据结构基础_数组】Leetcode 48.旋转图像

原题链接：Leetcode 48. Rotate Image

You are given an n x n 2D matrix representing an image, rotate the image by 90 degrees (clockwise).

You have to rotate the image in-place, which means you have to modify the input 2D matrix directly. DO NOT allocate another 2D matrix and do the rotation.

Example 1:

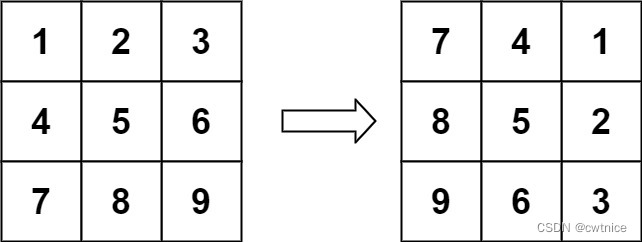
Input: matrix = [[1,2,3],[4,5,6],[7,8,9]]
Output: [[7,4,1],[8,5,2],[9,6,3]]
1
2

Example 2:

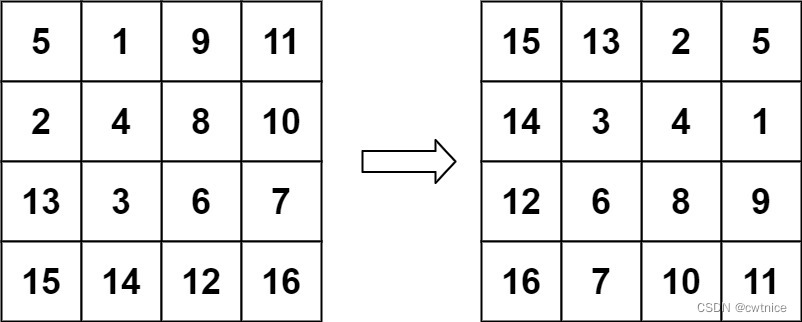
Input: matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
Output: [[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
1
2

Constraints:

• n == matrix.length == matrix[i].length
• 1 <= n <= 20
• -1000 <= matrix[i][j] <= 1000

---

方法一：原地旋转

思路：

问题的关键就是在于 如何防止覆盖 、 确定旋转的范围
那么可以用一个临时变量来暂存一个结点的值来防止覆盖
画图来确定旋转的范围：

当n为偶数时：

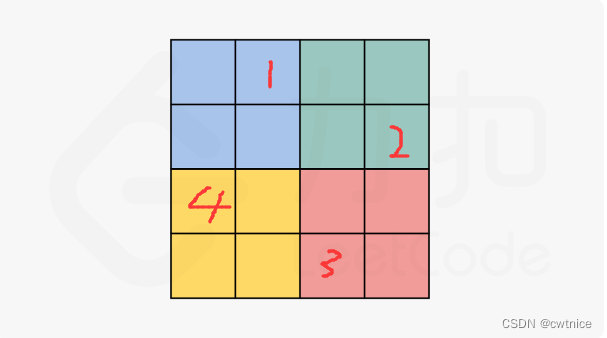
旋转 i = n/2, j = n/2的区间

当n为奇数时：

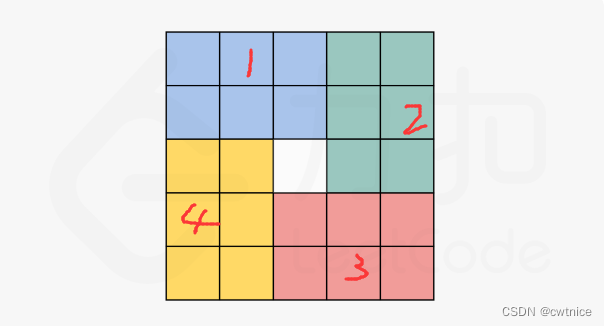
旋转 i = n/2，j = (n+1)/2的区间，最中间的白色部分不需要旋转

C++代码：

class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        // n边长
        int n = matrix.size();

        for (int i = 0; i < n / 2; ++i) {
            for (int j = 0; j < (n + 1) / 2; ++j) {
                // tmp用于暂存
                int temp = matrix[i][j];
                
                matrix[i][j] = matrix[n - j - 1][i];
                matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1];
                matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1];
                matrix[j][n - i - 1] = temp;
            }
        }
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

复杂度分析：

• 时间复杂度：O(n²)，两重循环，i和j都是和n相关
• 空间复杂度：O(1)，常数个临时变量