-
GAMES 101 笔记
GAMES 101 闫令琪 Lecture2-Linear Algebra 笔记。
如图1,
b ⃗ ⊥ = b ⃗ ⋅ a ⃗ ∥ a ⃗ ∥ b ⃗ \vec{b}_{\perp}=\frac{\vec{b}\cdot \vec{a}}{\| \vec{a}\|}\vec{b} b⊥=∥a∥b⋅ab
三角形的高
h ⃗ = b ⃗ − b ⃗ ⊥ \vec{h}=\vec{b}-\vec{b}_{\perp} h=b−b⊥
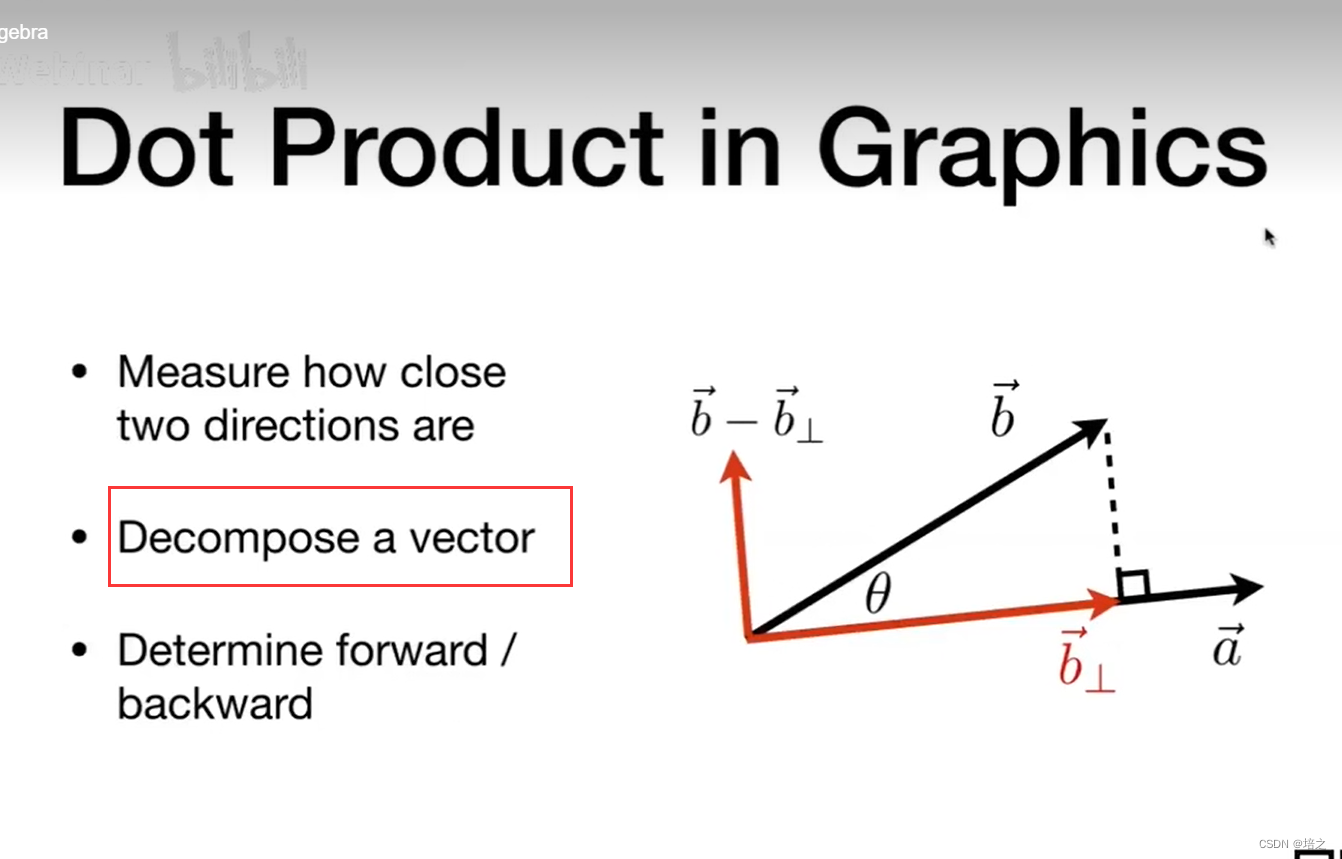
图1. 如图2,向量点乘可以判断夹角是否大于 9 0 ∘ 90^{\circ} 90∘。在某些场景下,夹角小于 9 0 ∘ 90^{\circ} 90∘有前向(可以看到的内涵),后向(看不到,被挡到的内涵)。
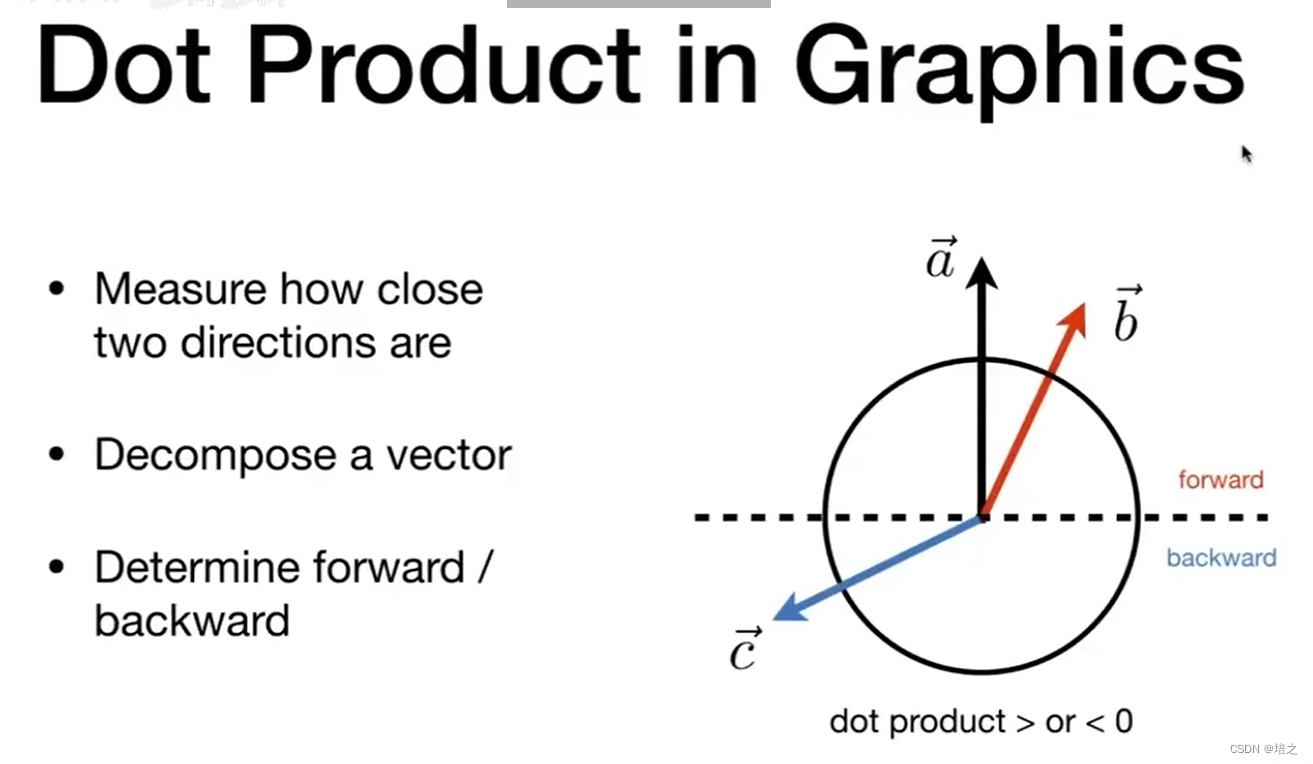
图2. 如图3,叉积可以决定两个向量相对的左右关系,也可以决定一个点在三角形内还是外的关系。
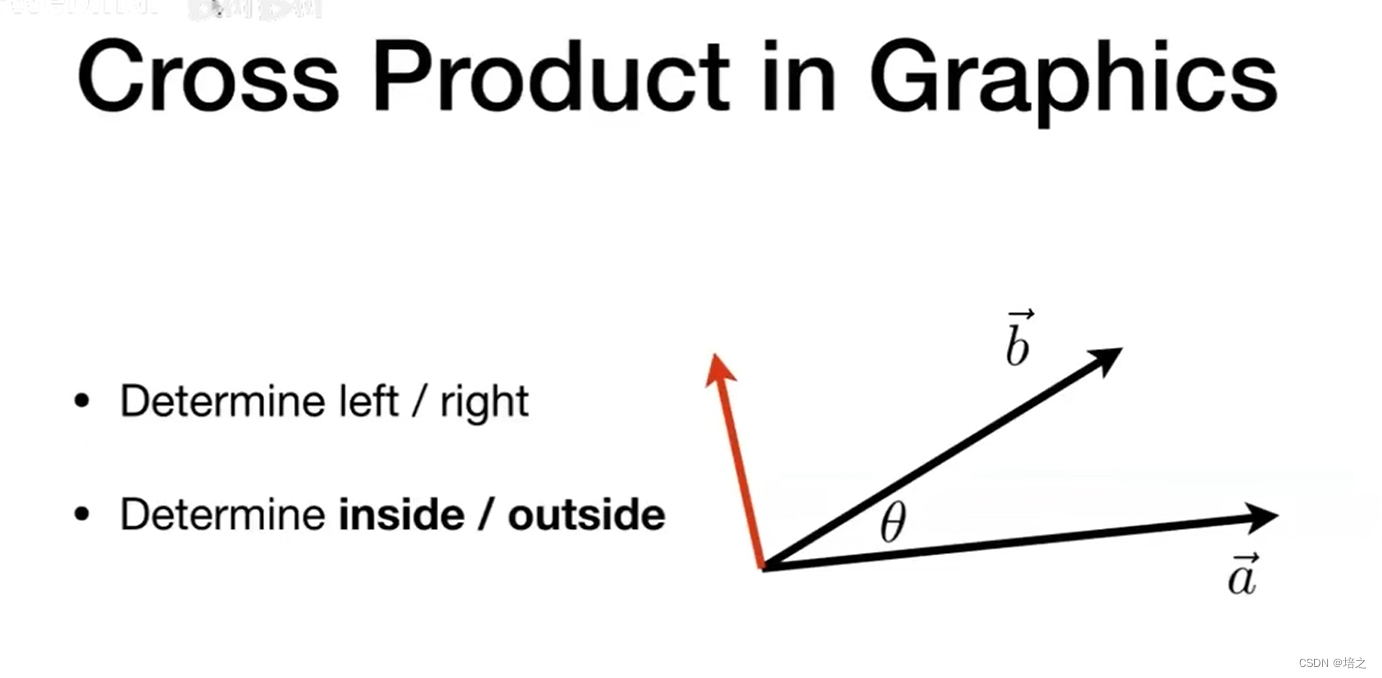
图3. 左图可以判断两个向量的左右相对关系
a ⃗ × b ⃗ \vec{a} \times \vec{b} a×b
如果叉乘得到的向量的 z 分量为正,则 a ⃗ \vec{a} a 在 b ⃗ \vec{b} b 右边右图可以判断 点 p是否在 三角形内:
依次做
A P ⃗ × A B ⃗ \vec{AP}\times\vec{AB} AP×AB
B P ⃗ × B C ⃗ \vec{BP}\times\vec{BC} BP×BC
C P ⃗ × C A ⃗ \vec{CP}\times\vec{CA} CP×CA
如果三个式子的结果的向量的 z 值正负号相同,即
A P B P C P AP \quad BP \quad CP APBPCP一直在左边,或者一直在右边,就是 P 在 △ A B C \triangle ABC △ABC内部。
反之,P 在 三角形 ABC 外部。corner case:自己决定,就是当点 P 在三角形边上的时候。
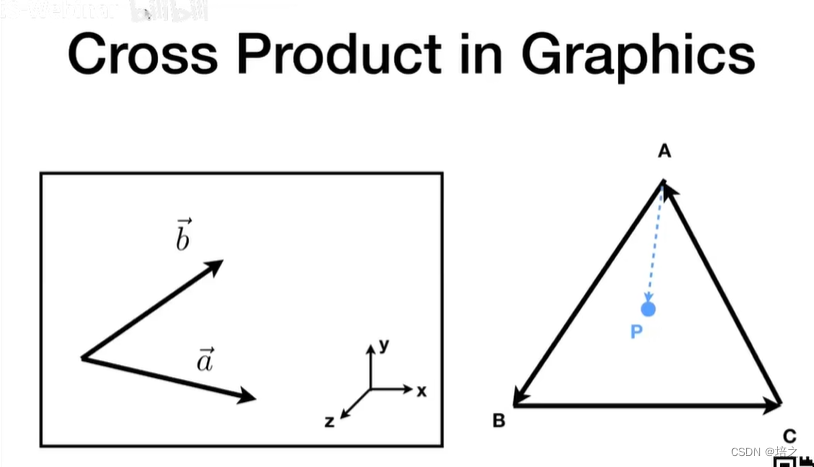
图4. 如图5,红色框框,框出来了用三个正交单位向量与內积来**坐标化向量**。
图5. -
相关阅读:
在 Vite项目中,使用插件 @rollup/plugin-inject 注入全局 jQuery
14条最佳JavaScript代码编写技巧
怎么获取 API Key:一步步指南
@MultipartConfig注解
动态表单开源库
Spring相关概念
2023年中国反射膜产量及市场规模分析:随着太阳能产业快速发展,规模持续扩大[图]
MnTTS: 开源蒙古语语音合成数据集及其基线模型
kubectl常用命令
PyQt5 的一些例子
- 原文地址:https://blog.csdn.net/OrdinaryMatthew/article/details/126002395