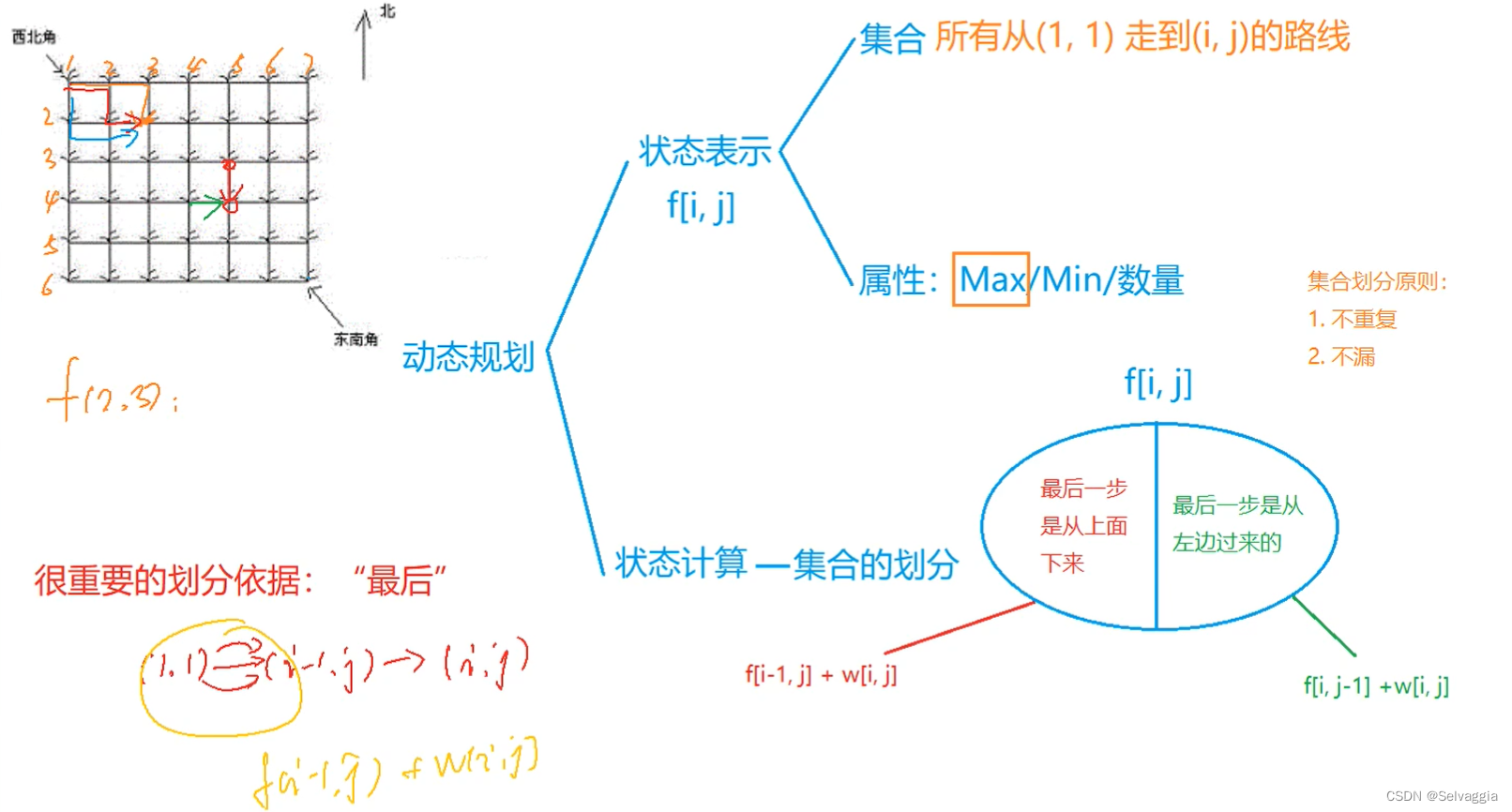
动态规划

1018. 最低通行费

注：注意属性，根据属性决定dp数组初始化的值

#include 
#include 
#include 
using namespace std; 
const int N=105;
int w[N][N];
int dp[N][N];
int main(){ 
		int n;
		cin>>n;
		for(int i=1;i<=n;i++){
			for(int j=1;j<=n;j++){
				cin>>w[i][j];
			}
		}
//		除了dp[1][1],第一行第一列的其他元素都不能从边界直接到达
		memset(dp,0x3f,sizeof(dp)); 
		for(int i=1;i<=n;i++){
			for(int j=1;j<=n;j++){
				if(i==1&&j==1)dp[i][j]=w[i][j];
				else dp[i][j]=min(dp[i-1][j],dp[i][j-1])+w[i][j];
				//这里求最小值，要考虑边界	 
			}
		}
		cout<<dp[n][n];

	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

1027. 方格取数⭐

不能计算分开两次最佳路线相加（第一次中相同程度的最佳路线有若干种选择，若两次分开考虑，第一次的选择可能会导致第二次受到限制） 主要原因是 只能向右或者向下
即，两个局部最优 不能确保 全局最优
同时计算的话，第一次的选择会对第二次的路线选择造成影响是可以在动态规划中体现的
如 样例

4
1 2 1
1 3 1
2 1 1
2 2 1
0 0 0
1
2
3
4
5
6

第一次局部最优，可以选择路线
1、（1，1）——>（1，4）——>（4，4）
2、（1，1）——>（1，2）——>（2，2）——>……
3、……
以上都是局部最优，但若选择第二种，那么结果只能是 2+1
但同时走，一定可以做到2+2

通过枚举横纵坐标之和 和两个横坐标，可以枚举两条路线同一时刻分别到达的所有点 
有点类似 区间dp，通过枚举 区间长度和区间起点，可以枚举到所有区间
动态规划 集合思想的精髓就在于 集合的最后一个元素，怎么走最后一步
两条路最终肯定同时到达(n,n),那么假设已知走完n-1步时 取到的最大结果是dp[2*n-1][i1][i2]
(两条路线分别到达(i1,j1),(i2,j2)) 
1
2
3
4
5

#include 
#include 
#include 
#include 
using namespace std; 
const int N=105;
int w[N][N];
int dp[N*2][N][N];
#define pii pair<int,int>
vector<pii> v;
int main(){ 
	int n;
	cin>>n;
	int a,b,c;
	while(cin>>a>>b>>c && (a||b||c)){
//		if(!a&&!b&&!c)break;
		w[a][b]=c;		
	}
	for(int k=2;k<=n+n;k++){//横纵行坐标之和即走过的步数 
		for(int i1=1;i1<=n;i1++){
			for(int i2=1;i2<=n;i2++){
				int j1=k-i1;
				int j2=k-i2;
				if(i1>=1&&j1<=n&&i2>=1&&j2<=n){
					int  t=w[i1][j1];
					if(i1!=i2)t+=w[i2][j2];
					int & x=dp[k][i1][i2];
					x=max(x,dp[k-1][i1-1][i2-1]+t);//右右 
					x=max(x,dp[k-1][i1-1][i2]+t);//右下 
					x=max(x,dp[k-1][i1][i2-1]+t);//下右 
					x=max(x,dp[k-1][i1][i2]+t);//下下 
				}
			}
		}
	}
	cout<<dp[n+n][n][n]; 
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

图论

单源最短路径

#include 
#include 
#include 
#include 
#define inf 0x3f3f3f3f
#define pii pair<int,int>
#include 
using namespace std; 
const int N=2505;
const int M=6205<<1;
struct edge{
	int to,w,nxt;
}e[M];
int head[N];
int cnt;
void add(int u,int v,int w){
	e[++cnt].w=w;
	e[cnt].to=v;
	e[cnt].nxt=head[u];
	head[u]=cnt;
}
int n,m,s,ee;
int dist[N];
int vis[N];
void dijikstra(int s){
	for(int i=1;i<=n;i++){
		vis[i]=0;
		dist[i]=inf;
	}
	dist[s]=0;
	priority_queue<pii,vector<pii>,greater<pii> >Q;
	Q.push({0,s});
	for(int t=0;t<n;t++){
		if(Q.empty()){
			return;
		}
		pii p=Q.top();Q.pop();
		int v=p.second;
		if(vis[v]){
			t--;
			continue;
		}
		vis[v]=1;
		for(int i=head[v];i;i=e[i].nxt){//链式前向星 找 节点v的邻接结点e[i] 
			int to=e[i].to;
			int w=e[i].w;
			if(!vis[to]&&dist[to]>dist[v]+w){
				dist[to]=dist[v]+w;
				Q.push({dist[to],to});
			}
		}
	}
}
int main(){ 

	cin>>n>>m>>s>>ee;
	int u,v,w;
	while(m--){
		cin>>u>>v>>w;
		add(u,v,w);
		add(v,u,w);
	}
	dijikstra(s);

	cout<<dist[ee];
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67