数学规划建模

txt文件的导入

filename = "C:\\Users\\LX\\Desktop\\model exercise\\0.txt";
a = Import[filename]；
a = Import[filename, "List"]；
a = Import[filename, "Table"]；

一个整数规划模型

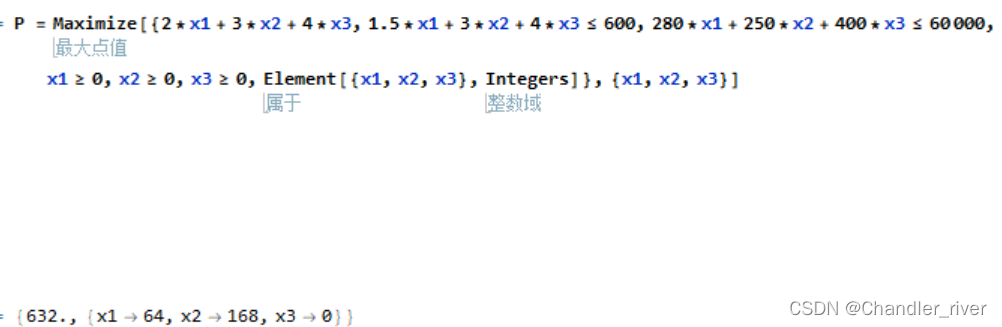
                max z=2x1+3x2+4x3

s.t.

        1.5 x1 + 3x2 + 4x3 <= 600

        280 x1 + 250 x2 + 400 x3 <= 60 000

        x1,x2,x3 >= 0  integer 

一个零一规划模型

        min z=

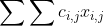
s.t.

        

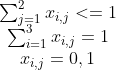
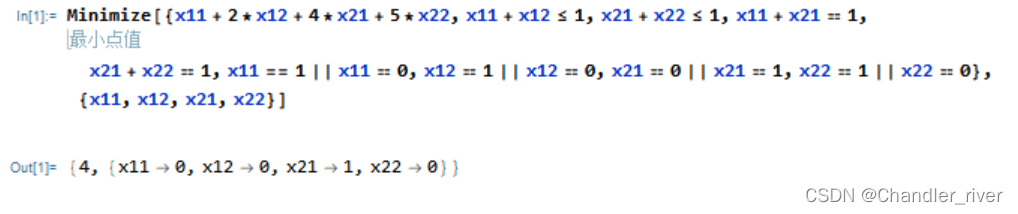
 解决实际问题----钢管下料问题

        原钢管长度均为19米，现需要50根4m，20根6m，15根8m，问下料方式

        求

        1：如何下料最节省

        2：在切割模式限定在三种以下，另外再要求切出10根5m钢管，如何下料更节省

        可列出全部可行的切割模式

问题一： 

决策变量  设xi表示按照第i种模式切割的原料钢管的数量，xi为非负的整数

约束条件        

        4m 50根        4x1 + 3x2 + 2x3 + x4 +x5 >= 50 

        6m 20            x2 + 2x4 + x5 +3x6 >=20 

        8m 15             x3 + x5 + 2x7 >= 15 

目标函数

        总余料最少

                min z = 3x1 + x2 +3x3 +3x4+ x5 + x6 + 3x7 

MMA操作

 问题二

决策变量

        用xi表示第i种模式切割的钢管数，

        r1i表示  4m  钢管   i种模式

        r2i表示  5m  钢管   i种模式  

约束条件

        几米的钢管要几根*4；

        切割模式必须合理   16<= 4r1i + 5r2i + 6r3i + 8r4i <= 19

        

目标函数

         所需钢管总数最少

同上题一样的............

微分方程建模

传染病建模

        SIS模型

模型假设

        1.总人数N不变，病人和健康人的比例分别为i(t),s(t)

        2.每个病人每天有效接触人数为λ，且使健康人致病

        3.每天被治愈的病人占病人总数u。病人治愈后任然可以被感染

        SIR模型

模型假设:治愈者不再感染

        1.总人数N不变，病人和健康人，移出者的比例分别为i(t),s(t),r(t)

        2.每个病人每天有效接触人数为λ，且使健康人致病

        3.每天被治愈的病人占病人总数u。病人治愈后任然可以被感染

有：

        

MMA解决

 

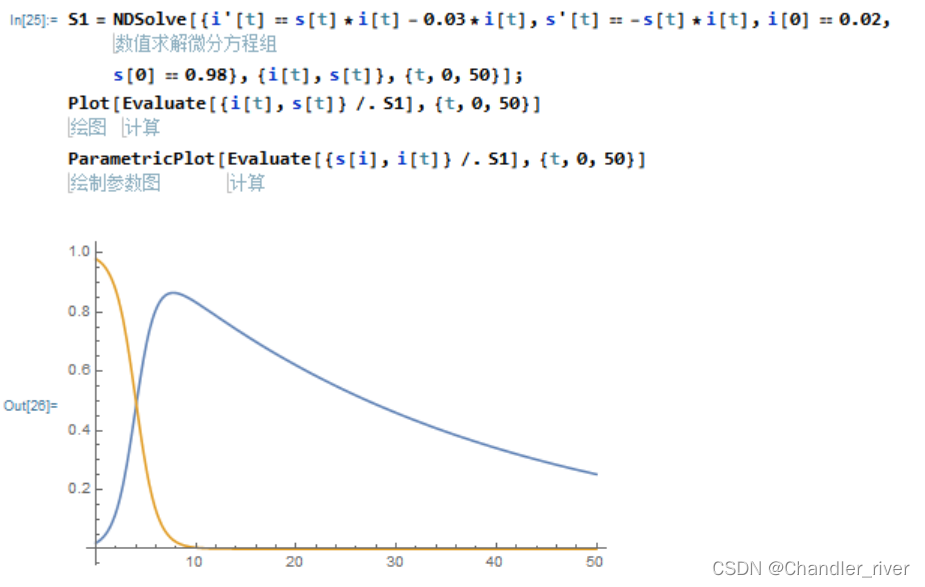
回归分析建模

        线性回归模型

1)数据采集

2)模型分析

(1散点图

(2以模型Y=b0+b1x+b2x^2+,

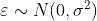
(3求回归方程y=b0+b1x+b2x^2,做回归分析

3)模型分析

(1 散点图

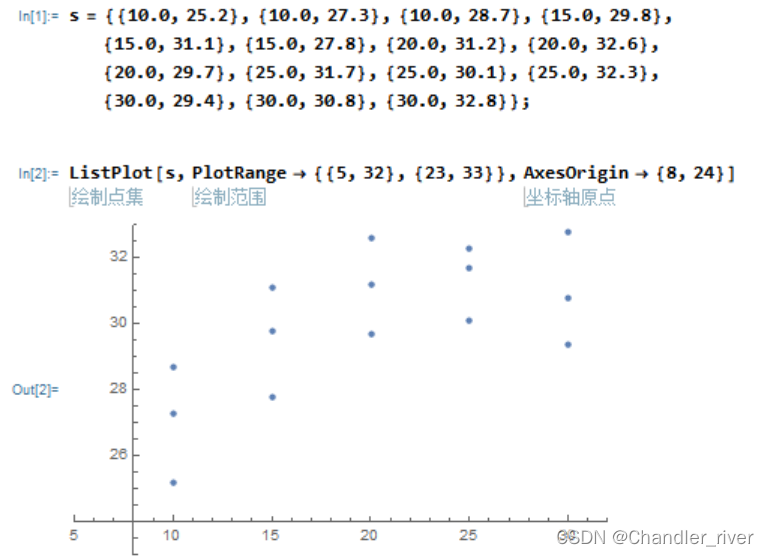
(2二元线性回归

 

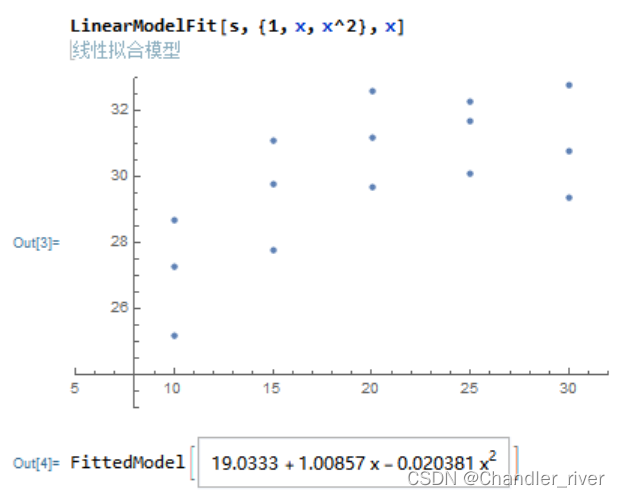
(3结果分析

离散建模

其他问题