数学知识——高斯消元（初等行变换解方程组）代码实现

高斯消元的作用：

求解n个未知数、n个方程的方程组

 例如如下n个方程、n个未知数：

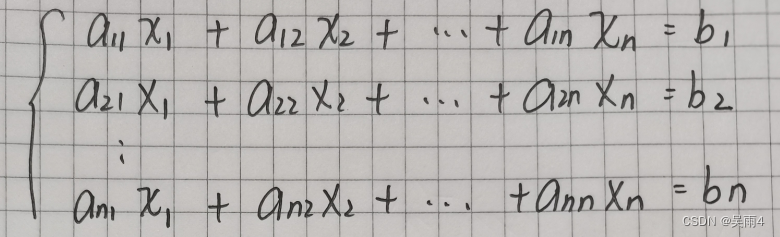
 写成n*（n+1）的矩阵：

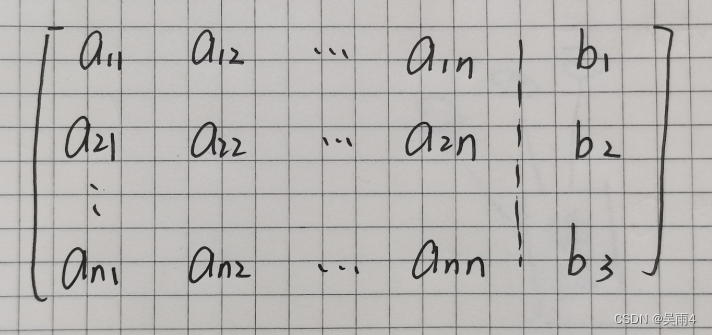
枚举每一列

第一步：找到绝对值最大的一行

第二步：将该行换到最上面

第三步：将该行的第一个数变成1

第四步：将下面行的此列变为0

注意的是，换好了的行不需要动！

 举一个例子：

求解有三个方程、三个未知数的方程组：

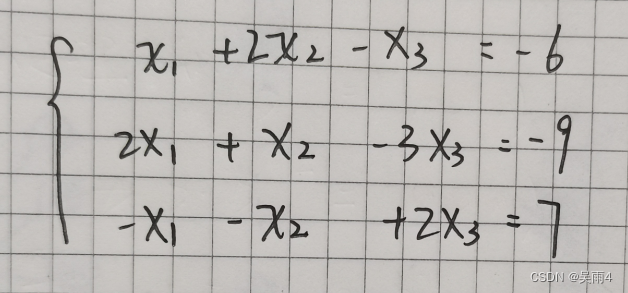
写成矩阵形式：

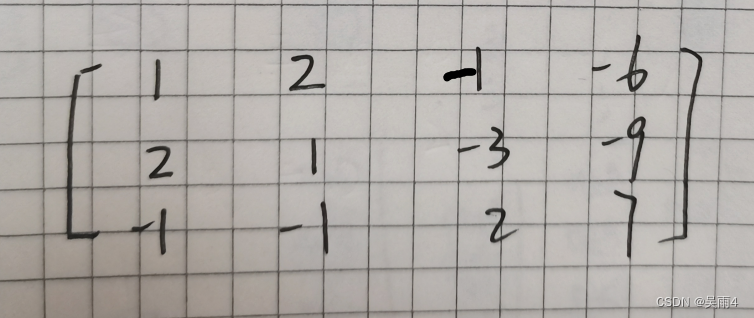
 枚举第一列，找到最大行：

 将该行换到最上面，并将该行第一个数变为1：

 将下面行的第1列都变成0：

 枚举第二列，找到绝对值最大的一行，将该行的第一个数变成1：

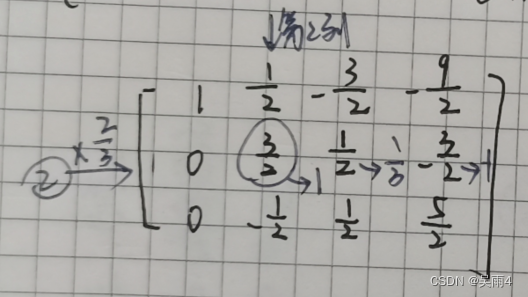
 将下面行的第1列都变成0：

 遍历第三列（由于第一行和第二行都已经改变好了，不需要动了），这里直接把第三行的第一个数变为1就行了：

 最后化简为：

由此可以依次算出：

x3=3；

x2=-2;

x1=3;

例题链接： 883. 高斯消元解线性方程组 - AcWing题库

 

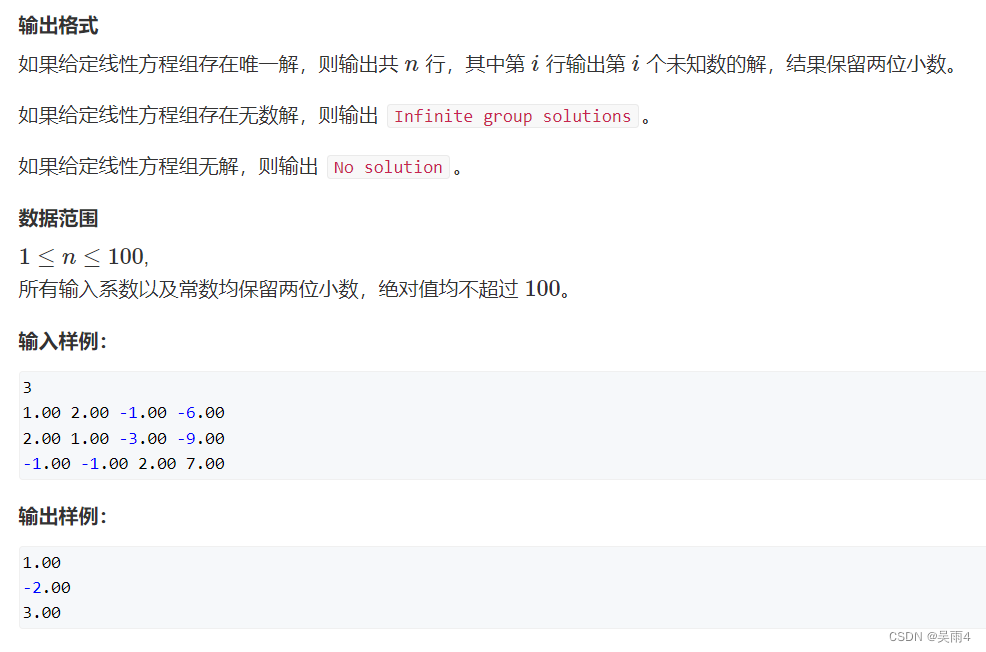
代码（详细注释）：

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
typedef long long ll;
const int N=110;
const double eps=1e-8;
int n;
double a[N][N];
int gauss()// 高斯消元，答案存于a[i][n]中，0 <= i < n
{
    int c,r;//c代表列，r代表行
    for(c=0,r=0;c<n;c++)//枚举每一列
    {
        int t=r;//存绝对值最大的行
        for(int i=r;i<n;i++)//找到绝对值最大的行
            if(fabs(a[i][c])>fabs(a[t][c])) t=i;
 
        if(fabs(a[t][c])<eps)//最大值为0
            continue;
 
        for(int i=c;i<=n;i++) swap(a[t][i],a[r][i]);// 将绝对值最大的行换到最顶端
 
		for(int i=n;i>=c;i--) a[r][i]/=a[r][c];//将当前行的首位变成1
 
		for(int i=r+1;i<n;i++)// 用当前行将下面所有的列消成0
            if(fabs(a[i][c])>eps)
                for(int j=n;j>=c;j--)
                    a[i][j]=a[i][j]-a[r][j]*a[i][c];
            r++;
    }
    if(r<n)
    {
    	for(int i=r;i<n;i++)
    		if(fabs(a[i][n])>eps) return 2;//无解
		return 1;//多解
	}
	for(int i=n-1;i>=0;i--)
		for(int j=i+1;j<n;j++)
			a[i][n]=a[i][n]-a[i][j]*a[j][n];
	return 0;
}
int main()
{
    IOS;
    cin>>n;
    for(int i=0;i<n;i++)
        for(int j=0;j<=n;j++)
            cin>>a[i][j];
 
    int t=gauss();
 
    if(t==2) cout<<"No solution"<<endl;//无解
 
    else if(t==1) cout<<"Infinite group solutions"<<endl;//多解
 
    else//唯一解
    {
        for(int i=0;i<n;i++)
        {
            if(fabs(a[i][n])<eps) a[i][n]=0;//去掉输出-0.00的情况
             printf("%.2lf\n", a[i][n]);
        }
    }
    return 0;
}