微分&导数&微商

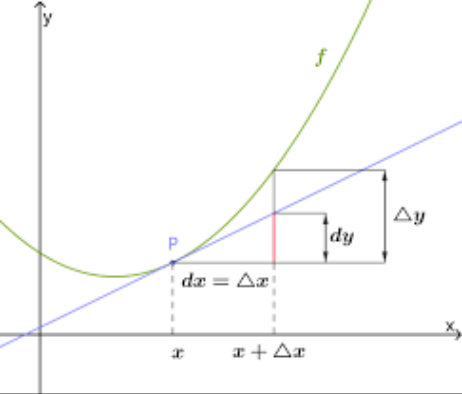
函数在$x=x_0$导数的定义

• 定义两点

A x 0 ( x 0 , f ( x 0 ) ) ; ( 指 定 x = x 0 处 的 极 限 ) B x = ( x , f ( x ) ) = ( x 0 + Δ x , f ( x 0 + Δ x ) ) { Δ x = x − x 0 Δ y = { f ( x ) − f ( x 0 ) f ( x 0 + Δ x ) − f ( x 0 ) x → x 0 ⟺ Δ x → 0 有 时 , 也 记 h = Δ x A_{x_0}(x_0,f(x_0));(指定x=x_0处的极限) \\ B_x=(x,f(x))=(x_0+\Delta x,f(x_0+\Delta x)) \\

\end{cases} \\ x\rightarrow x_0 \Longleftrightarrow \Delta x\rightarrow 0 \\有时,也记h=\Delta x Ax0​​(x0​,f(x0​));(指定x=x0​处的极限)Bx​=(x,f(x))=(x0​+Δx,f(x0​+Δx))⎩⎪⎨⎪⎧​Δx=x−x0​Δy={f(x)−f(x0​)f(x0​+Δx)−f(x0​)​​x→x0​⟺Δx→0有时,也记h=Δx

lim ⁡ Δ x → 0 Δ y Δ x = { lim ⁡ Δ x → 0 f ( x 0 + Δ x ) − f ( x 0 ) Δ x lim ⁡ x → x 0 f ( x ) − f ( x 0 ) x − x 0 lim ⁡ h → 0 f ( x 0 + h ) − f ( x 0 ) h \lim_{\Delta x\rightarrow 0}{\frac{\Delta y}{\Delta x}} =

Δx→0lim​ΔxΔy​=⎩⎪⎪⎪⎨⎪⎪⎪⎧​Δx→0lim​Δxf(x0​+Δx)−f(x0​)​x→x0​lim​x−x0​f(x)−f(x0​)​h→0lim​hf(x0​+h)−f(x0​)​​

通常,为了方便书写,经常采用第三中形式进行推导:
$$f^{\prime }(x_0)=\underset{h\to 0}{\lim }\frac{f(x_0+h)-f(x_0)}{h}$$

导函数的定义

• 和导数的定义类似,我们将导数定义中的$x_0$替换为x

• $$f^{\prime }(x)=\underset{\Delta x\to 0}{\lim }\frac{f(x+\Delta x)-f(x)}{\Delta x}=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x)}{h}$$

  记
  $$g(h)=\frac{f(x+h)-f(x)}{h}$$

  则
  $$\begin{gathered} f^{\prime }(x)=\underset{\Delta x\to 0}{\lim }g(\Delta x)=\underset{h\to 0}{\lim }g(h) \\ 这里这么写,是为了强调,利用导数定义求导数(导函数)的时候, \\ 被求极限的函数g(h)的自变量h(即f(x)自变量x的增量\Delta x)与被求导数的f(x)的自变量x不同 \end{gathered}$$

• 显然,$f(x)在x_0处的导数f^{\prime }(x_0)就是导函数f^{\prime }(x)在x=x_0处的函数值$

  • $$f^{\prime }(x_0)=f^{\prime }(x){|}_{x=x_0}=\frac{dx}{dy}$$

对数函数的导数推导(导数定义极限法)

$$\begin{gathered} f(x)=lo{g}_{a}x \\ {f}^{\prime }(x)=(lo{g}_{a}x{)}^{\prime }=\underset{h\to 0}{\lim }\frac{lo{g}_a(x+h)-lo{g}_a(x)}{h}=\underset{h\to 0}{\lim }\frac{lo{g}_a(\frac{x+h}{x})}{h} \\ =\underset{h\to 0}{\lim }\frac{1}{h}lo{g}_a(x+hx) \\ =\underset{h\to 0}{\lim }lo{g}_a(1+\frac{h}{x}{)}^{\frac{1}{h}} \\ 记g(h)=lo{g}_a(1+\frac{h}{x}{)}^{\frac{1}{h}} \\ (lo{g}_{a}x{)}^{\prime }=\underset{h\to 0}{\lim }g(h);g(h)的自变量是h(g(h)将x看作常量) \\ 该极限是1^{\infty }类型;由第二重要极限的推广公式得到:A=\underset{h\to 0}{\lim }\frac{h}{x}\frac{1}{h}=\frac{1}{x} \\ 所以对于u=\varphi (h)=(1+\frac{h}{x}{)}^{\frac{1}{h}}; \\ {u}_0=\underset{h\to 0}{\lim }u=e^{\frac{1}{x}} \\ 又由复合函数的极限运算法则:\underset{h\to 0}{\lim }g(h)=\underset{u\to u_0}{\lim }lo{g}_{a}u=lo{g}_a{u}_0=lo{g}_a{e}^{\frac{1}{x}} \\ 根据换底公式得到(lo{g}_{a}x{)}^{\prime }=lo{g}_a{e}^{\frac{1}{x}}=\frac{\ln e^{\frac{1}{x}}}{\ln a}=\frac{1}{x}\frac{1}{\ln a} \end{gathered}$$

导数与微分

• 微分是导数的另一种描述形式
• 导数$y^{\prime }=\frac{dy}{dx}$,(函数的微分dy除以自变量x的微分dx,因而导数也叫做微商)

对数函数的导函数

$$(lo{g}_{a}x{)}^{\prime }=\frac{1}{x\ln a}$$

• 对数函数的导函数可以通过第二重要极限计算得到

反函数求导法

$以a^x的导函数推导为例,利用反函数求导法则$

• 直接函数

  • $$\begin{gathered} x=x(y)=lo{g}_{a}y \\ x,y取值范围: \\ y\in (0,+\infty ) \\ x\in (-\infty ,+\infty ) \\ (自变量y的)函数x的导数: \\ {x}^{\prime }(y)=\frac{1}{y}\frac{1}{\ln a} \end{gathered}$$

• 反函数

  • $$\begin{gathered} y=y(x)=a^x \\ ★函数x(y)和函数y(x)互为反函数 \end{gathered}$$

• 反函数的导数

  • $$\begin{gathered} 则:y^{\prime }(x)=\frac{1}{x^{\prime }(y)}=\frac{1}{\frac{1}{x\ln a}}=x\ln a \\ 即,y^{\prime }(x)=(a^x{)}^{\prime }=x\ln a \\ \therefore (a^x{)}^{\prime }=x\ln a \end{gathered}$$

对数求导法

$以求a^x的导函数为例,使用对数求导法(伯努利求导法)$

$$\begin{gathered} y=a^x \\ \ln y=\ln a^x=x\ln a \\ 两边同时求导 \\ \frac{1}{y}{y}^{\prime }=\ln a \\ {y}^{\prime }=y\ln a=a^x\ln a \\ 即,(a^x{)}^{\prime }=a^x\ln a \end{gathered}$$