一、统计的基本概念

1、统计学含义

统计学是一门收集、处理、分析、理解数据并从数据中心得出结论的科学

统计学分析步骤（核心：数据）

收集数据→处理数据→分析数据（描述性统计分析、推理性统计分析）→解释数据数据

2、统计学分析数据的方法

描述性分析

研究数据收集、处理和描述的统计学方法

总体规模、对比关系、集中趋势、离散程度、偏态、峰态、……

推断性分析

研究如何利用样本数据来推断总体特征额统计学方法

估计、假设检验、列联分析、方差分析、相关分析、回归分析、……

3、统计学应用

随着计算机的发展及各种统计软件的开发，作为一门基础学科的统计学在金融、保险、生物、经济等领域得到了广泛应用。

4、统计学的基本概念-数据

统计学的对象是数据。

数据的形式

数字：可以进行比较、加减乘除等运算，严格的数据符号，常用阿拉伯数字表示

文字：不可运算，如男、女等

数据的分类

数据的其他分类

5、统计学的基本概念-总体和样本

• 总体（population）

指研究的所有元素的集合，其中每个元素成为个体。

如：现研究全校学生的平均年龄，总体是：全校学生和总体相关的事物，统计学上用希腊字母表示。

• 样本（sample）

从总体中抽取的一部分元素的集合。

如：为研究全校学生的平均年龄，由于总体太大，从中抽取100人进行研究，该研究中的样本是抽取的这100个学生。

和样本相关的事物，统计学生用英文字母表示。

所有和总体有关的东西都是一个定值，所有和样本有关的东西都是一个变量。

构成样本的元素的数目称为样本容量。

6、统计学的基本概念-参数和统计量

• 参数（parameter）

指研究者想要了解的总体的某种特征值

主要有总体均值（μ）、总体标准差（σ）、总体比例（π）等

• 统计量（statistics）

指根据样本数据计算出来的一个量，即样本的某个特征值；

常见的统计量有样本均值（X̅）、样本标准差（s）、样本比例（p）等。

7、统计学的基本概念-变量

• 变量

指描述事物某种特征的概念。如商品销售额、受教育程度、产品的质量等级等。

• 变量与数据的关系

变量的具体表现称为变量值，即数据。

• 变量的分类

根据变量的数据计量尺度不同来分

分类变量（categorical variable）：说明事物类别的一个名称

顺序变量（rank variable）：说明事物有序类别的一个名称

数值型变量（metric variable）：说明事物数字特征的一个名称

二、数据的描述性统计

总体规模的描述——总量指标

反映在一定时间、空间条件下某种现象的总体规模、总水平或总成果的统计指标。如：营业额、利润

对比关系的描述——相对指标

是两个有相互联系的指标数值之比。

如：目标完成率（实际完成/计划完成）

集中趋势的描述——平均指标

集中趋势（Central tendency）：一组数据向其中心值靠拢的趋势

测度集中趋势就是寻找数据水平的代表值或中心值

分类型数据可用 众数

顺序型数据可用 众数、分位数

数值型数据可用 众数、分位数、均值

众数：出现次数最多的变量值，表示符号Mo，计算：寻找数据中出现次数最多的值（众数的不唯一性）

分位数：是指根据对数据位置进行划分，处于某些特定位置上的数，常用的分位数有二分位数（也叫“中位数”）、四分位数、十分位数、百分位数等

中位数（二分位数）：数据排序后，处于中间位置上的值表示符号Me，计算：数据的个数为n，则中位数的位置=（n+1）/2，偶数个数据的中位数为中间两数平均值，奇数个数据的中位数为最中间的数值四分位数：分为下四分位数和上四分位数两种，指排序后处于25%和75%位置上的值，表示的符号为下四分位数Ql，上四分位数Qu，计算：数据的个数为n，则下四分位数Ql的位置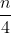：，上四分位数Qu的位置：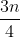

 

均值（mean）

• 算术平均数：数据的和与数据个数之比，表示的符号：X̅，特点：易受极端值影响

简单算术平均数（根据未分组数据计算的）：X̅=（X1+X2+...+Xn）/n

加权算术平均数（根据分组数据计算的）：X̅=(X1f1+X2f2+...+Xkfk)/（f1+f2+...+fk）

（其中：数据个数为n，分组数据的组数为k，Mi为组中值，fi为各组的频数。）

• 几何平均数：n个变量值乘积的n次方根，表示符号：G，特点：易受极端值影响，常用于增长率数据的研究，所有数据需大于0

简单调和平均数（根据未分组数据计算的）：G=

加权调和平均数（根据分组数据计算的）：G=

（其中，数据个数为n，分组数据的组数为k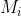，为组中值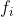，为各组的频数。）

调和平均数

离散程度的描述——变异指标

分布形态的描述——偏态与峰态

描述性统计图表

三、统计分布

四、相关分析