• 数据结构“入门”—堆的实现

    一、堆的概念和结构

    1：堆的概念

    上文中我们已经提到过，堆是一个按照完全二叉树的储存方式顺序储存在一个一维数组中的结构。

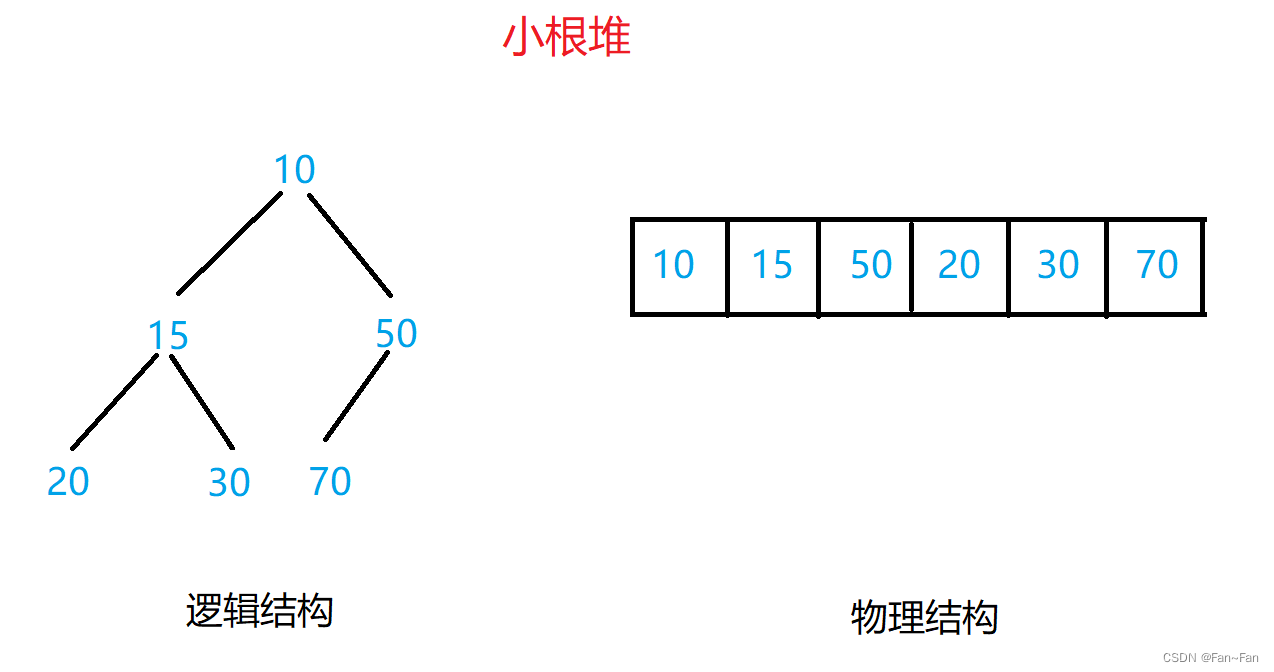
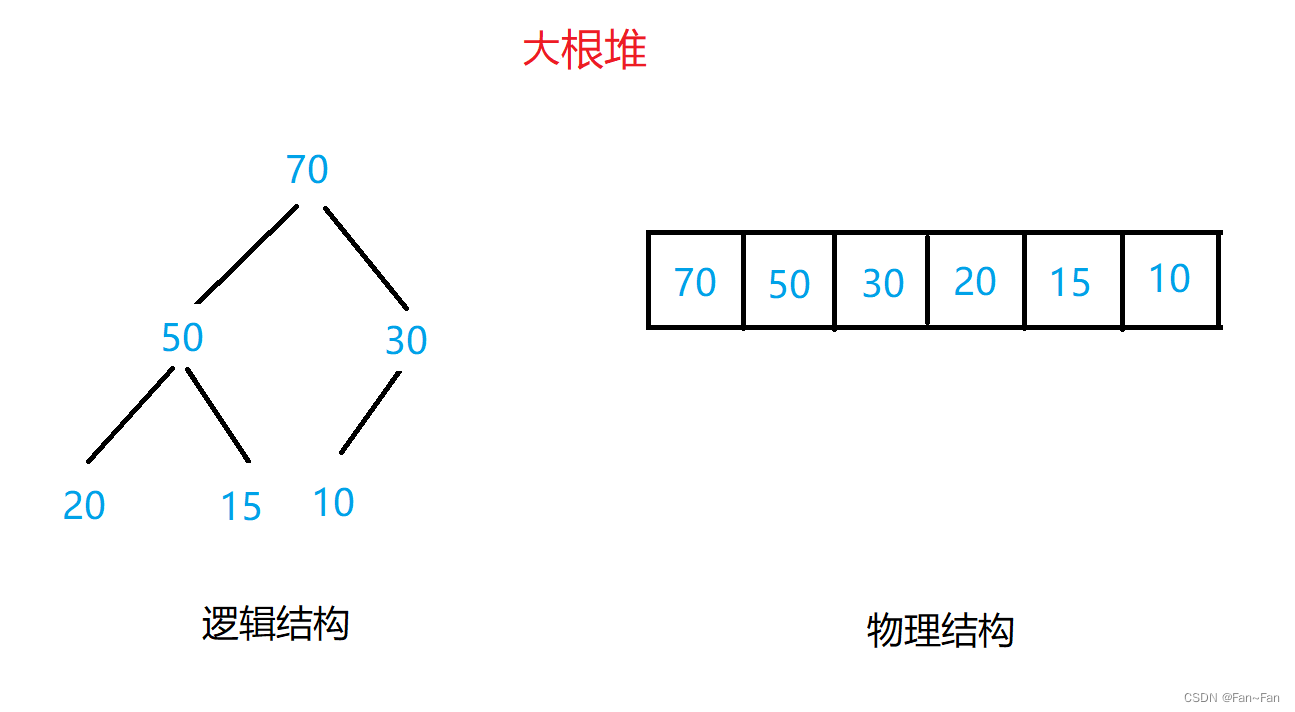
    堆：如果有一个关键码的集合K = {k0,k1,k2,k3…k(n-1)}，把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并满足:Ki<=K(2*i+1)且Ki<=K(2*i+2) {Ki>=K(2*i+1)且Ki>=K(2*i+2)} i = 0，1， 2…,则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。

    1.小堆：每一个父结点的值均小于或等于其子结点的值，且其根结点的值是最小的。

    2.大堆：每一个父结点的值均大于或等于其子结点的值，且其根结点的值是最大的。

     · 堆的性质：

    1. 堆中某个节点的值总是不大于或不小于其父节点的值；

    2. 堆总是一棵完全二叉树。

    2:堆的结构 

      

    二、堆的实现 

    1：堆的简单接口实现

    创建堆结构

    ·思路：

    堆是用数组实现的，所以创建堆结构实质上就是开辟一个动态数组。

    · Heap.h文件：

    1. //创建堆结构(以小堆为例)
    2. typedef int HPDataType;  //堆中储存数据类型
    3.  
    4. typedef struct Heap
    5. {
    6. 	HPDataType* a;    //数组地址
    7. 	size_t size;      //记录堆中有效数据个数
    8. 	size_t capacity;  //记录堆的容量
    9. }HP;

    初始化堆 

    ·思路：

    初始化堆和之前初始化顺序表，栈等都是同样的道理。

    · Heap.h文件：

    1. //初始化堆
    2. void HeapInit(HP* php);

    · Heap.c文件：

    1. //初始化堆
    2. void HeapInit(HP* php)
    3. {
    4. 	assert(php);  //传过来的结构体指针不能为空
    5. 	php->a = NULL;
    6. 	php->size = php->capacity = 0;
    7. }

    堆的打印 

    ·思路：

    堆的物理结构是数组，所以打印堆实质上就是打印顺序表。

    · Heap.h文件：

    1. //堆的打印
    2. void HeapPrint(HP* php);

    · Heap.c文件：

    1. //堆的打印
    2. void HeapPrint(HP* php)
    3. {
    4. 	assert(php);
    5. 	for (size_t i = 0; i < php->size; i++)
    6. 	{
    7. 		printf("%d ", php->a[i]);
    8. 	}
    9. 	printf("\n");
    10. }

    堆的销毁 

    ·思路：

    free掉动态开辟的内存

    · Heap.h文件：

    1. //堆的销毁
    2. void HeapDestory(HP* php);

    · Heap.c文件：

    1. //堆的销毁
    2. void HeapDestory(HP* php)
    3. {
    4. 	assert(php);
    5. 	free(php->a);
    6. 	php->a = NULL;
    7. 	php->size = php->capacity = 0;
    8. }

    堆的数据交换 

    ·思路：

    思路和交换两个整型数据一样，同时记得传地址。

    · Heap.h文件：

    1.  
    2. //数据交换
    3. void Swap(HPDataType* pa, HPDataType* pb);

    · Heap.c文件：

    1. //数据交换
    2. void Swap(HPDataType* pa, HPDataType* pb)
    3. {
    4. 	HPDataType tmp = *pa;
    5. 	*pa = *pb;
    6. 	*pb = tmp;
    7. }

    堆的判空 

    ·思路：

    判断size是否为0,如果size为0则说明堆中无元素，堆为空。

    · Heap.h文件：

    1. //堆的判空
    2. bool HeapEmpty(HP* php);

    · Heap.c文件：

    1. //堆的判空
    2. bool HeapEmpty(HP* php)
    3. {
    4. 	assert(php);
    5. 	return php->size == 0;
    6. }

    获取堆中元素个数

     ·思路：

    堆中元素个数也就是size的值。

    · Heap.h文件：

    1. //获取堆中元素个数
    2. size_t HeapSize(HP* php);

    · Heap.c文件：

    1. //获取堆中元素个数
    2. size_t HeapSize(HP* php)
    3. {
    4. 	assert(php);
    5. 	return php->size;
    6. }

    获取堆顶的元素 

    ·思路：

    获取堆顶元素之前首先需要确定堆不为空。也就是当size>0的前提下返回堆顶元素。

    · Heap.h文件：

    1. //获取堆顶元素
    2. HPDataType HeapTop(HP* php);

    · Heap.c文件：

    1. //获取堆顶元素
    2. HPDataType HeapTop(HP* php)
    3. {
    4. 	assert(php);
    5. 	assert(php->size > 0);
    6. 	return php->a[0];
    7. }

    2：堆的核心接口实现 

    堆的向上调整算法(从下往上调整）

    ·思路：

    堆的向上调整算法是为了当我们向堆中插入一个数据后，堆的结构仍然不发生改变，大堆依然是大堆，小堆依然是小堆。

    举个例子：假如我们向下图中的小堆中插入一个10。

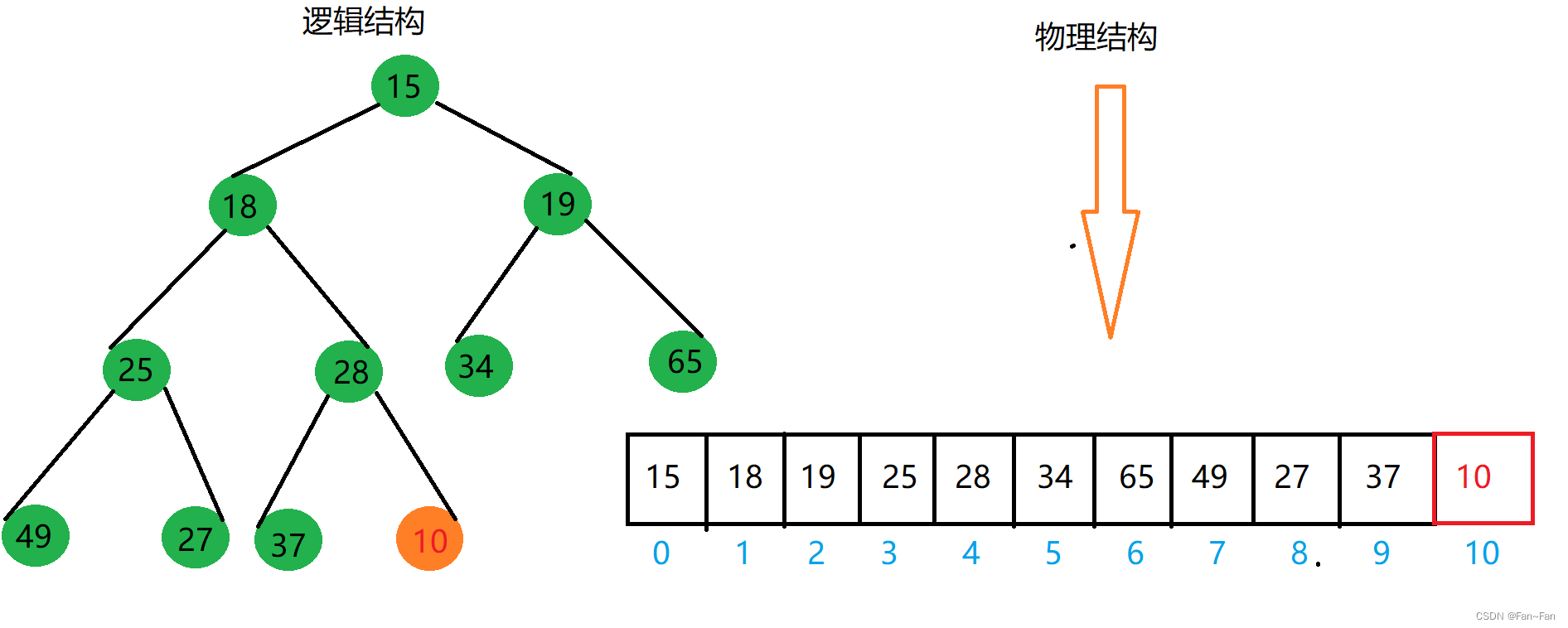
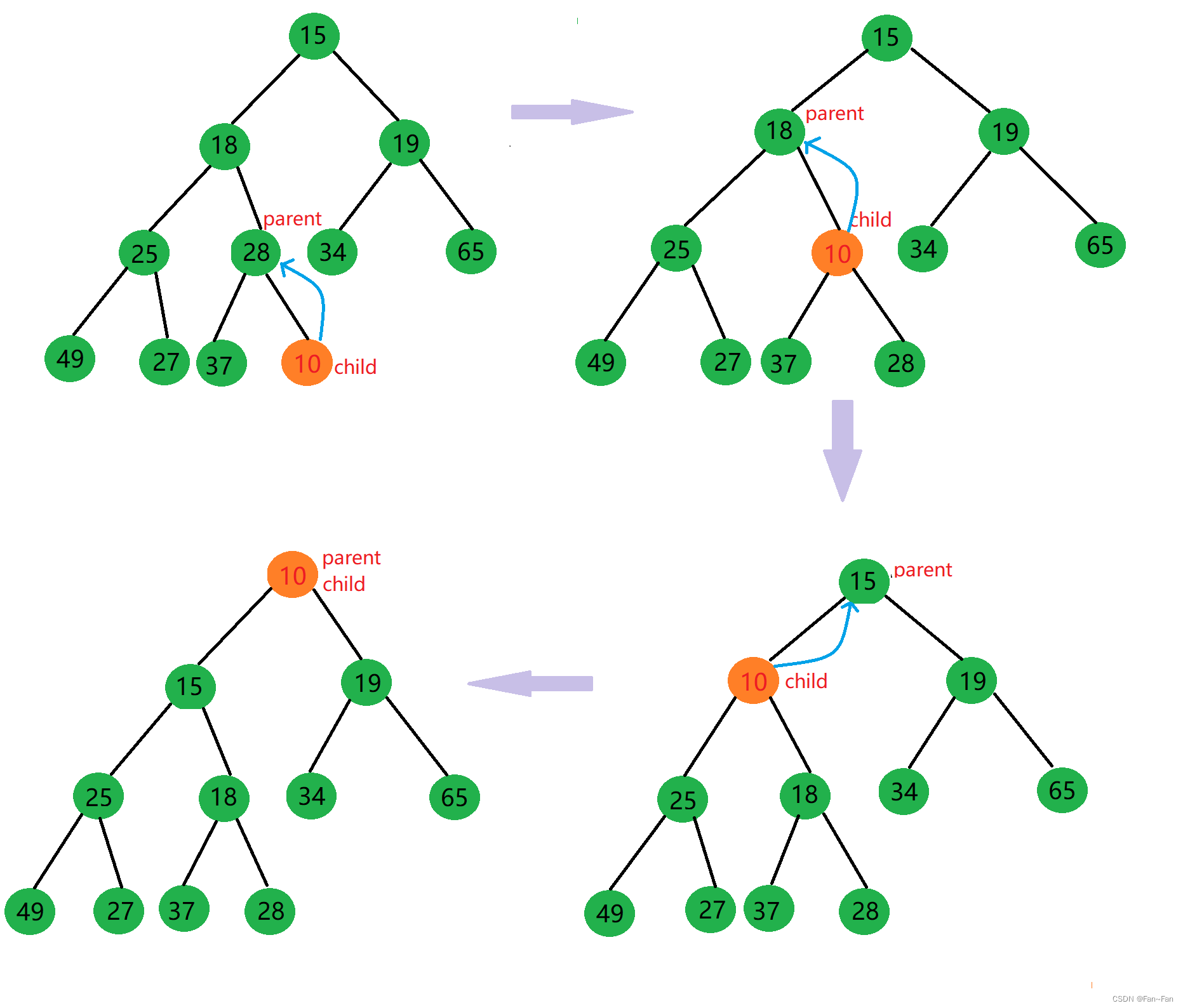
     我们向小根堆中插入10,插入后孩子结点10<父结点28,这破坏了小根堆结构，所以此时我们就需要向上调整，依次比较父结点parent和子结点child的大小，当父结点小于子结点就结束，反之就一直交换结点数据，直到根部。

    父结点与子结点关系：parent=(child-1)/2

    ✈交换过程如下图所示✈：

     · Heap.h文件：

    1. //堆的向上调整算法
    2. void AdjustUp(HPDataType* a, size_t child);

    · Heap.c文件：

    1. //堆的向上调整算法
    2. void AdjustUp(HPDataType* a, size_t child)
    3. {
    4. 	size_t parent = (child - 1) / 2;
    5. 	while (child > 0)
    6. 	{
    7. 		//if(a[child]>a[parent]) //大根堆
    8. 		if (a[child] < a[parent])   //小根堆
    9. 		{
    10. 			Swap(&a[child], &a[parent]);
    11. 			child = parent;
    12. 			parent = (child - 1) / 2;
    13. 		}
    14. 		else
    15. 		{
    16. 			break;
    17. 		}
    18. 	}
    19. }

    堆的向下调整算法(从上往下调整）

    ·思路：

    1、找出左右孩子结点中较小的那一个

    2、较小的孩子结点与父结点比较，如果孩子结点比父亲结点小，交换数据

    3、重复向下调整

    举个例子：假如我们要调整下面的堆

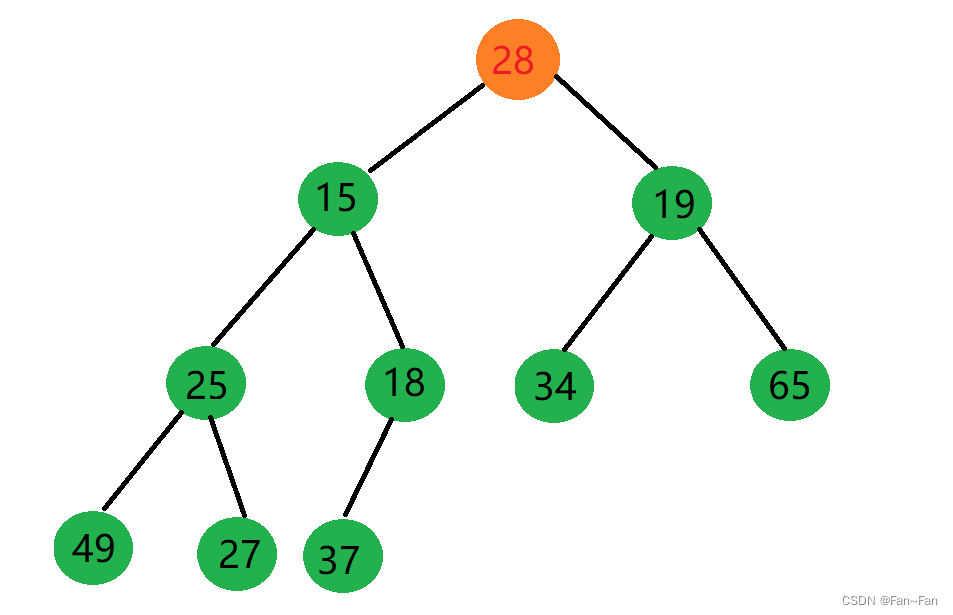
     ✈交换过程如下图所示✈：

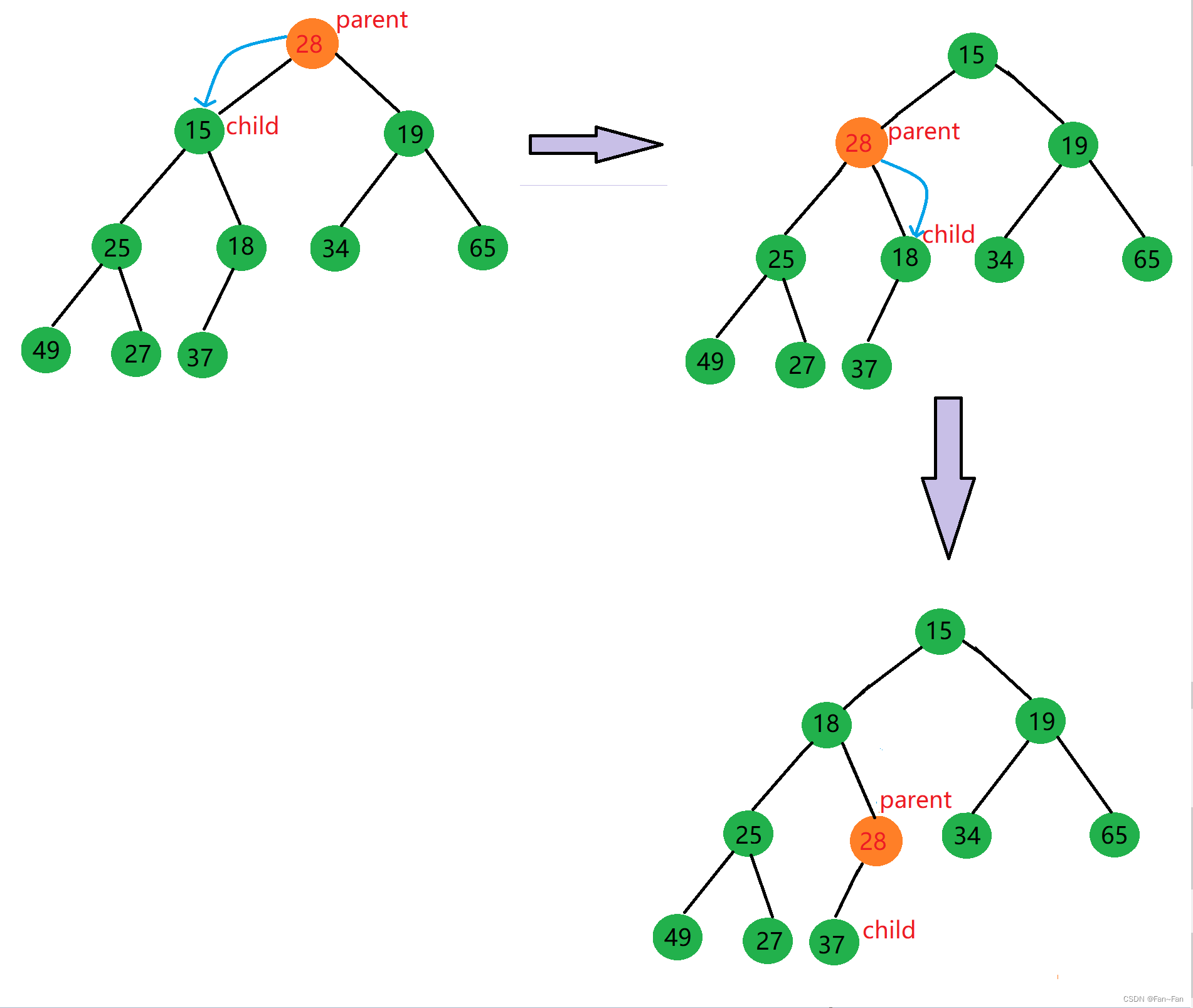
     · Heap.h文件：

    1. //堆的向下调整算法
    2. void AdjustDown(HPDataType* a, size_t size, size_t root);

    · Heap.c文件：

    1. //堆的向下调整算法
    2. void AdjustDown(HPDataType* a, size_t size, size_t root)
    3. {
    4. 	int parent = root;
    5. 	int child = 2 * parent + 1;   //默认较小孩子结点为左孩子结点
    6. 	while (child < size)
    7. 	{
    8. 		//确保child对应的值为较小孩子结点的值
    9. 		if (child + 1 < size && a[child + 1] < a[child])  //确保右孩子结点在堆得的范围内
    10. 		{
    11. 			child++; //此时child中存的值为右孩子结点中的值
    12. 		}
    13. 		//如果孩子结点小于父亲结点则交换，并继续向下调整
    14. 		if (a[child] < a[parent])
    15. 		{
    16. 			Swap(&a[child], &a[parent]);
    17. 			parent = child;
    18. 			child = 2 * parent + 1;
    19. 		}
    20. 		//如果孩子结点大于父亲结点，则结束调整
    21. 		else
    22. 		{
    23. 			break;
    24. 		}
    25. 	}
    26.  
    27. }

    堆的插入 

    ·思路：

    虽然堆的物理结构是一个数组，但因为其逻辑结构是一个完全二叉树，所以当我们插入数据只能进行尾插。尾插后可能结构发生改变，这时候我们就需要进行向上调整，使堆恢复原来的结构。

    举个例子：假如我们向下图中的小堆中插入一个10。

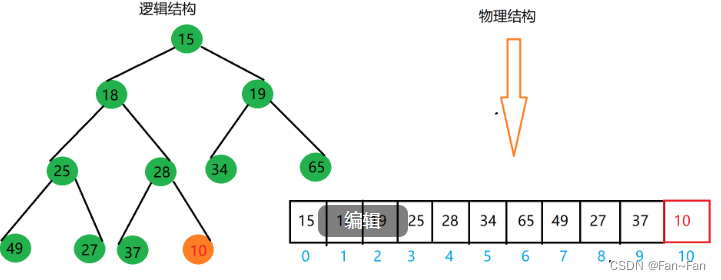
    步骤：

    1：检查扩容：和顺序表一样，当我们插入一个数据后我们首先要做的就是检查是否需要扩容。

    2：调整堆结构：插入10以后我们可以发现子结点10小于父结点28，堆的结构遭到破环，此时我们就需要将10进行向上调整。

     · Heap.h文件：

    1. //堆的插入
    2. void HeapPush(HP* php, HPDataType x);

    · Heap.c文件：

    1. //堆的插入
    2. void HeapPush(HP* php, HPDataType x)
    3. {
    4. 	assert(php);
    5. 	//检查是否需要扩容
    6. 	if (php->size == php->capacity)
    7. 	{
    8. 		size_t newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;
    9.  
    10. 		HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity);
    11. 		if (tmp == NULL)
    12. 		{
    13. 			printf("realloc fail\n");
    14. 			exit(-1);
    15. 		}
    16. 		php->a = tmp;
    17. 		php->capacity = newcapacity;
    18.  
    19. 	}
    20. 	php->a[php->size] = x;
    21. 	php->size++;
    22. 	//调整堆结构
    23. 	AdjustUp(php->a, php->size - 1);
    24. }

    ✈下面我们来测试一下✈：

    · Test.c文件：

    1. void TestHeap()
    2. {
    3. 	HP hp;
    4. 	HeapInit(&hp);
    5. 	//插入数据
    6. 	HeapPush(&hp, 1);
    7. 	HeapPush(&hp, 5);
    8. 	HeapPush(&hp, 3);
    9. 	HeapPush(&hp, 0);
    10. 	HeapPush(&hp, 8);
    11. 	HeapPush(&hp, 9);
    12.  
    13. 	//打印
    14. 	HeapPrint(&hp);
    15. 	//销毁
    16. 	HeapDestory(&hp);
    17.  
    18. }

    测试效果：

     

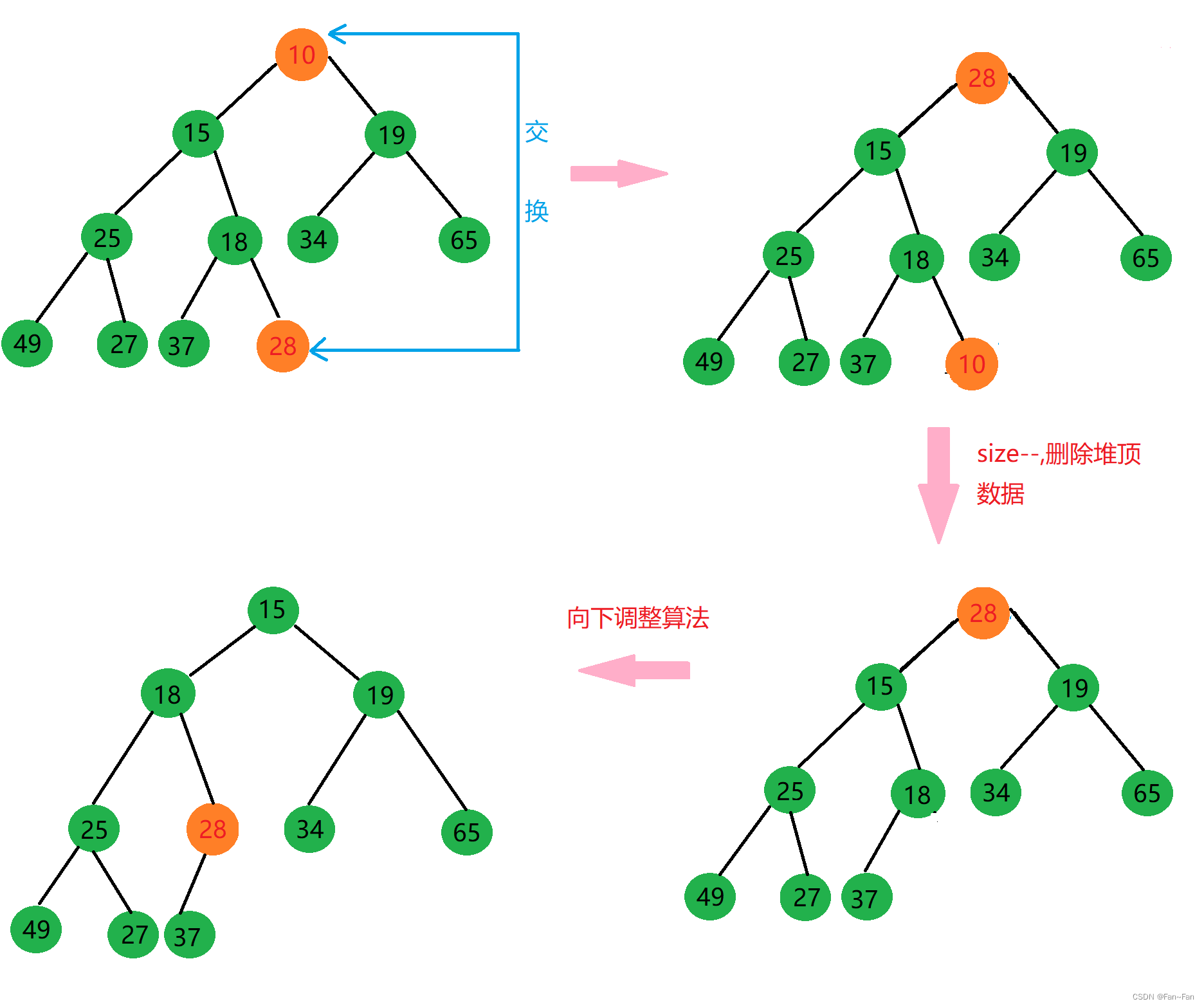
    堆的删除

    ·思路：

    向堆中插入数据后需要保持堆的结构不发生改变，同理在堆中删除数据后我们仍需要使堆的结构不发生改变。所不一样的是在堆中插入数据我们是从尾部插入，而从堆中删除数据我们是从堆顶删除。

    步骤：

    First：把堆顶数据与堆中最后一个数据进行交换

    Next：size--,删除掉堆顶数据。

    Last ：运用向下调整算法，确保其仍是堆结构

    举个例子：假如我们删除下图小堆中的堆顶元素。

      ✈交换过程如下图所示✈：

     ‼⚠：时间复杂度分析

    第一个数据和最后一个数据进行交换，时间复杂度为O(1)。因为向下调整的次数是树的深度，所以向下调整算法的时间复杂度为O(logN)，所以总的时间复杂度为O(logN)。

    · Heap.h文件：

    1. //堆的删除
    2. void HeapPop(HP* php);

    · Heap.c文件：

    1. //堆的删除
    2. void HeapPop(HP* php)
    3. {
    4. 	assert(php);
    5. 	assert(php->size > 0);  //确保堆中有元素
    6. 	Swap(&php->a[0], &php->a[php->size - 1]); //交换堆头和堆尾的数据
    7. 	php->size--;  //删除掉堆顶数据
    8. 	//向下调整，确保堆结构
    9. 	AdjustDown(php->a, php->size, 0);
    10.  
    11. }

    ✈下面我们来测试一下✈：

    · Test.c文件：

    1. void TestHeap2()
    2. {
    3. 	HP hp;
    4. 	HeapInit(&hp);
    5. 	//插入数据
    6. 	HeapPush(&hp, 1);
    7. 	HeapPush(&hp, 5);
    8. 	HeapPush(&hp, 3);
    9. 	HeapPush(&hp, 0);
    10. 	HeapPush(&hp, 8);
    11. 	HeapPush(&hp, 9);
    12.  
    13. 	//打印
    14. 	HeapPrint(&hp);
    15.  
    16. 	//删除堆顶数据
    17. 	HeapPop(&hp);
    18. 	HeapPrint(&hp);
    19. 	//销毁
    20. 	HeapDestory(&hp);
    21.  
    22. }

    测试效果：

     我们可以发现删除前后都还是小根堆。

     三、总代码

     Heap.h文件

    1. #pragma once
    2. #include <stdio.h>
    3. #include <stdlib.h>
    4. #include <assert.h>
    5. #include <stdbool.h>
    6.  
    7. //创建堆结构(以小堆为例)
    8. typedef int HPDataType;  //堆中储存数据类型
    9.  
    10. typedef struct Heap
    11. {
    12. 	HPDataType* a;    //数组地址
    13. 	size_t size;      //记录堆中有效数据个数
    14. 	size_t capacity;  //记录堆的容量
    15. }HP;
    16. //初始化堆
    17. void HeapInit(HP* php);
    18.  
    19. //堆的打印
    20. void HeapPrint(HP* php);
    21.  
    22. //堆的销毁
    23. void HeapDestory(HP* php);
    24.  
    25. //数据交换
    26. void Swap(HPDataType* pa, HPDataType* pb);
    27.  
    28. //堆的判空
    29. bool HeapEmpty(HP* php);
    30.  
    31. //获取堆中元素个数
    32. size_t HeapSize(HP* php);
    33.  
    34. //获取堆顶元素
    35. HPDataType HeapTop(HP* php);
    36.  
    37. //堆的向上调整算法
    38. void AdjustUp(HPDataType* a, size_t child);
    39.  
    40. //堆的向下调整算法
    41. void AdjustDown(HPDataType* a, size_t size, size_t root);
    42.  
    43. //堆的插入
    44. void HeapPush(HP* php, HPDataType x);
    45.  
    46. //堆的删除
    47. void HeapPop(HP* php);

    Heap.c文件

    1. #include "Heap.h"
    2.  
    3. //初始化堆
    4. void HeapInit(HP* php)
    5. {
    6. 	assert(php);  //传过来的结构体指针不能为空
    7. 	php->a = NULL;
    8. 	php->size = php->capacity = 0;
    9. }
    10.  
    11. //堆的打印
    12. void HeapPrint(HP* php)
    13. {
    14. 	assert(php);
    15. 	for (size_t i = 0; i < php->size; i++)
    16. 	{
    17. 		printf("%d ", php->a[i]);
    18. 	}
    19. 	printf("\n");
    20. }
    21.  
    22. //堆的销毁
    23. void HeapDestory(HP* php)
    24. {
    25. 	assert(php);
    26. 	free(php->a);
    27. 	php->a = NULL;
    28. 	php->size = php->capacity = 0;
    29. }
    30.  
    31. //数据交换
    32. void Swap(HPDataType* pa, HPDataType* pb)
    33. {
    34. 	HPDataType tmp = *pa;
    35. 	*pa = *pb;
    36. 	*pb = tmp;
    37. }
    38.  
    39. //堆的判空
    40. bool HeapEmpty(HP* php)
    41. {
    42. 	assert(php);
    43. 	return php->size == 0;
    44. }
    45.  
    46. //获取堆中元素个数
    47. size_t HeapSize(HP* php)
    48. {
    49. 	assert(php);
    50. 	return php->size;
    51. }
    52.  
    53. //获取堆顶元素
    54. HPDataType HeapTop(HP* php)
    55. {
    56. 	assert(php);
    57. 	assert(php->size > 0);
    58. 	return php->a[0];
    59. }
    60.  
    61. //堆的向上调整算法
    62. void AdjustUp(HPDataType* a, size_t child)
    63. {
    64. 	size_t parent = (child - 1) / 2;
    65. 	while (child > 0)
    66. 	{
    67. 		//if(a[child]>a[parent]) //大根堆
    68. 		if (a[child] < a[parent])   //小根堆
    69. 		{
    70. 			Swap(&a[child], &a[parent]);
    71. 			child = parent;
    72. 			parent = (child - 1) / 2;
    73. 		}
    74. 		else
    75. 		{
    76. 			break;
    77. 		}
    78. 	}
    79. }
    80.  
    81. //堆的向下调整算法
    82. void AdjustDown(HPDataType* a, size_t size, size_t root)
    83. {
    84. 	int parent = root;
    85. 	int child = 2 * parent + 1;   //默认较小孩子结点为左孩子结点
    86. 	while (child < size)
    87. 	{
    88. 		//确保child对应的值为较小孩子结点的值
    89. 		if (child + 1 < size && a[child + 1] < a[child])  //确保右孩子结点在堆得的范围内
    90. 		{
    91. 			child++; //此时child中存的值为右孩子结点中的值
    92. 		}
    93. 		//如果孩子结点小于父亲结点则交换，并继续向下调整
    94. 		if (a[child] < a[parent])
    95. 		{
    96. 			Swap(&a[child], &a[parent]);
    97. 			parent = child;
    98. 			child = 2 * parent + 1;
    99. 		}
    100. 		//如果孩子结点大于父亲结点，则结束调整
    101. 		else
    102. 		{
    103. 			break;
    104. 		}
    105. 	}
    106.  
    107. }
    108.  
    109. //堆的插入
    110. void HeapPush(HP* php, HPDataType x)
    111. {
    112. 	assert(php);
    113. 	//检查是否需要扩容
    114. 	if (php->size == php->capacity)
    115. 	{
    116. 		size_t newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;
    117.  
    118. 		HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity);
    119. 		if (tmp == NULL)
    120. 		{
    121. 			printf("realloc fail\n");
    122. 			exit(-1);
    123. 		}
    124. 		php->a = tmp;
    125. 		php->capacity = newcapacity;
    126.  
    127. 	}
    128. 	php->a[php->size] = x;
    129. 	php->size++;
    130. 	//调整堆结构
    131. 	AdjustUp(php->a, php->size - 1);
    132. }
    133.  
    134. //堆的删除
    135. void HeapPop(HP* php)
    136. {
    137. 	assert(php);
    138. 	assert(php->size > 0);  //确保堆中有元素
    139. 	Swap(&php->a[0], &php->a[php->size - 1]); //交换堆头和堆尾的数据
    140. 	php->size--;  //删除掉堆顶数据
    141. 	//向下调整，确保堆结构
    142. 	AdjustDown(php->a, php->size, 0);
    143.  
    144. }

    Test.c文件

    1. #include "Heap.h"
    2. void TestHeap1()
    3. {
    4. 	HP hp;
    5. 	HeapInit(&hp);
    6. 	//插入数据
    7. 	HeapPush(&hp, 1);
    8. 	HeapPush(&hp, 5);
    9. 	HeapPush(&hp, 3);
    10. 	HeapPush(&hp, 0);
    11. 	HeapPush(&hp, 8);
    12. 	HeapPush(&hp, 9);
    13.  
    14. 	//打印
    15. 	HeapPrint(&hp);
    16. 	//销毁
    17. 	HeapDestory(&hp);
    18.  
    19. }
    20.  
    21. void TestHeap2()
    22. {
    23. 	HP hp;
    24. 	HeapInit(&hp);
    25. 	//插入数据
    26. 	HeapPush(&hp, 1);
    27. 	HeapPush(&hp, 5);
    28. 	HeapPush(&hp, 3);
    29. 	HeapPush(&hp, 0);
    30. 	HeapPush(&hp, 8);
    31. 	HeapPush(&hp, 9);
    32.  
    33. 	//打印
    34. 	HeapPrint(&hp);
    35.  
    36. 	//删除堆顶数据
    37. 	HeapPop(&hp);
    38. 	HeapPrint(&hp);
    39. 	//销毁
    40. 	HeapDestory(&hp);
    41.  
    42. }
    43.  
    44. int main()
    45. {
    46. 	TestHeap2();
    47.  
    48. 	return 0;
    49. }
  • 相关阅读:
    Excel VLOOKUP 使用记录
    SpringBoot3之Web编程
    白盒测试设计方法
    stm32cubemx hal学习记录：FreeRTOS软件定时器
    性能评测|影驰RTX4090金属大师系列显卡正式发售!
    深入理解操作系统-进程篇
    【负优化】如何理解Android手机系统升级时，反而“负优化”？ | 附：国产AI大模型列表 | 人的真实注意力相关：为什么有时候一直看一个汉字，反而感觉不认识这个汉字了呢？
    Java基础 进程与线程3
    第二十章《Java Swing》第7节：对话框
    Oracle19c单实例数据库配置OGG单用户数据同步测试
  • 原文地址：https://blog.csdn.net/weixin_60718941/article/details/125584631