一、实验目的

掌握算符优先语法分析

二、实验题目

三、分析与设计

3.1 基础知识部分

根据优先关系表，对任意符号串每一步识别可归约符号串，即最左素短语进行归约，逐步到归约到文法的开始符号，从而判断其是否符合语法。

素短语：是指这样一种短语，它至少包含一个终结符，并且除自身之外，不再包含其它更小的素短语。

最左素短语：句型最左边的那个素短语。

3.2 分析步骤

判断给定的文法是否是OPG文法：
1）产生式右部不含两个相邻的非终结符
2）任意两算符之间最多只存在一种优先关系

对文法的每个非终结符P构造FIRSTVT( P ) 集合和LASTVT( P ) 集合

构造算符优先分析表

四、源代码

#include <iostream>
#include <fstream>
#include <string>
#include <cstring>
#include <conio.h>
#include <stack>
#include <map>
#include <vector>
#include <unordered_map>
#define digit 1 // 1数字
#define op 2 // +-*/()#
#define Hh 3 // 3Hh
#define AF 4 // 4A-F
#define letter 5 // 5其它字母
using namespace std;
const int N = 8;

typedef struct node {
	char data;
	struct node* before;
	struct node* next;
};

node* temp, * top;
string line;

char q; // 指向输入符号串中当前的字符
char word[20]; // 存储当前识别的单词
int state; // 表示所处的状态
int i; // 单词的下标

// 存储算法优先关系表
// 大于关系为1，等于关系为0，小于关系为-1，出错为9
// 顺序：+, -, *, /, i, (, ), #
int table[N][N] = {
	{1, 1, -1, -1, -1, -1, 1, 1},
	{1, 1, -1, -1, -1, -1, 1, 1},
	{1, 1, 1, 1, -1, -1, 1, 1},
	{1, 1, 1, 1, -1, -1, 1, 1},
	{1, 1, 1, 1, 9, 9, 1, 1},
	{-1, -1, -1, -1, -1, -1, 0, 9},
	{1, 1, 1, 1, 9, 9, 1, 1},
	{-1, -1, -1, -1, -1, -1, 9, 0}
};

void push(char c); // 入栈
char pop(); // 出栈
int t2j(char current); // 将字符数字化
int parser(string line);
bool check_terminal(char ch); // 判断是否是终结符
int isDigitOrChar(char ch);
string change_i(string words); // 将含有十进制或十六进制数的表达式转换为用i代替的表达式

int main() {
	//打开文件 
	ifstream fin("test.txt");
	if (!fin.is_open()) {
		cout << "open file error." << endl;
		_getch();
		return -1;
	}

	while (getline(fin, line)) {
		//逐行读取 
		string temp = line;
		//转换为i字符串 
		line = change_i(line);
		if (line == "-1") {
			cout << temp << " is not a valid express." << endl;
			puts("--------------------------------");
			continue;
		}
		cout << "Output string is: " << line << endl;
		 
		top = NULL;
		top = (node*)malloc(sizeof(node));
		top->before = NULL;
		top->next = NULL;
		top->data = ' ';

		cout << "Start parse string " << line << ":" << endl << endl;
		//开始分析 
		parser(line);
		puts("--------------------------------");
	}

	return 0;
}

void push(char c) {  // 入栈函数
	temp = (node*)malloc(sizeof(node));

	temp->data = c;
	temp->before = top;
	temp->next = NULL;

	top->next = temp;  // 双向链表
	top = temp;
}

char pop() {
	char ch = top->data;

	if (top->before != NULL) {
		temp = top;
		top = temp->before;
		temp->before = NULL;
		top->next = NULL;
		free(temp);
	}

	return ch;
}

int t2j(char current) {
	// 顺序：+, -, *, /, i, (, ), #
	int j = 0;

	switch (current) {
	case '+': j = 0; break;
	case '-': j = 1; break;
	case '*': j = 2; break;
	case '/': j = 3; break;
	case 'i': j = 4; break;
	case '(': j = 5; break;
	case ')': j = 6; break;
	case '#': j = 7;
	}

	return j;
}

void showMess(int l, string line) {

	node* t = top;
	vector<char> v;
	while (t) {
		v.push_back(t->data);
		t = t->before;
	}

	string str;
	for (int i = v.size() - 1; i >= 0; i--) {
		str += v[i];
	}
	cout << str;

	cout << "\t\t";
	for (int i = l; i < line.size(); i++) {
		cout << line[i];
	}
	cout << "\t\t";

}

int parser(string line) {
	int i, j;
	push('#');

	int k = 1;

	bool flag = true;
	// line[l] != '#'
	for (int l = 0; ; l++) {
		showMess(l, line);

		// 退出条件
		if (top->data == 'N' && top->before->data == '#' && line[l] == '#') break;

		node* sktemp = top;
		char sk = top->data;
		char a = line[l];
		// 任何两终结符之间最多只有一非终结符，若非终结符往前寻找一位即可
		if (!check_terminal(sk)) {
			sk = top->before->data;
			sktemp = top->before;
		}
		i = t2j(sk); // 获取栈顶终结符
		j = t2j(a); // 获取当前输入符号
		switch (table[i][j]) {
		case 9:  // 语法错误
			flag = false;
			break;
		case 0:
			cout << "=" << "\t\t" << "push in" << endl;
			push(a);
			break;
		case -1:  // 小于，移进
			cout << "<" << "\t\t" << "push in" << endl;
			push(a);
			break;
		case 1:   // 大于，归约
			cout << ">" << "\t\t" << "reduce" << endl;
			node* Q = sktemp;
			node* sj = sktemp;
			do {
				sj = Q;
				if (check_terminal(Q->before->data)) Q = Q->before;
				else Q = Q->before->before;
			} while (table[t2j(Q->data)][t2j(sj->data)] == 0);
			//Q++;
			while (top != Q) 
				char c = pop();
			
			push('N');
			l--;

			break;
		}
		if (!flag) break;
	}

	if (!flag) 
		cout << endl << line << " is not valid." << endl;
	else 
		cout << endl << line << " is valid." << endl;

	return 1;
}

int isDigitOrChar(char ch) {
	if (ch >= 48 && ch <= 57) // 数字
		return digit;
	else if (ch == 72 || ch == 104) // H or h
		return Hh;
	else if ((ch >= 65 && ch <= 70) || (ch >= 97 && ch <= 102)) // 字母A,B,C,D,E,F
		return AF;
	else if ((ch >= 65 && ch <= 90) || (ch >= 97 && ch <= 122)) // 除A~F外的其它字母
		return letter;
	else if (ch == '+' || ch == '-' || ch == '*' || ch == '/' || ch == '(' || ch == ')' || ch == '#')
		return op;
}

// 将含有十进制或十六进制数的表达式转换为用i代替的表达式
string change_i(string words) {
	memset(word, 0, sizeof word);
	state = 0;
	i = 0;
	cout << "Input string is: " << words << endl;

	string result = "";
	int cnt = 0;
	q = words[cnt++];

	while (cnt <= words.size()) {
		// 先判断状态，再判断字符
		switch (state) {
		case 0: // 0状态
			switch (isDigitOrChar(q)) {
			case digit: // 数字
				word[i++] = q;
				state = 2; // 转移到2状态
				break;
			case Hh: // H or h
			case AF: // 字母A,B,C,D,E,F or a,b,c,d,e,f
			case letter: // 字母
				word[i++] = q;
				state = 1;
				break;
			case op: // 操作符
				result += q;
				state = 0;
				break;
			default: // 其它（非法字符 ）
				word[i++] = q;
				state = 5;
			}
			break;
		case 1: // 1状态
			switch (isDigitOrChar(q)) {
			case Hh: // 当前状态遇到字母、数字往下读入
			case AF:
			case digit:
			case letter:
				word[i++] = q;
				state = 1;
				break;
			case op: // 读入完毕，识别为标识符
				word[i] = '\0';
				printf("%s is an identifier.\n", word);
				//result += "i";
				memset(word, 0, sizeof word);
				i = 0;
				state = 0;
				result = "-1";
				return result;
				break;
			default:
				word[i++] = q;
				state = 5;
			}
			break;
		case 2: // 2状态
			switch (isDigitOrChar(q)) {
			case digit: // 若为数字，不改变状态往下读入
				word[i++] = q;
				state = 2;
				break;
			case Hh: // 若为Hh，转移至状态3
				word[i++] = q;
				state = 3;
				break;
			case AF: // 若为AF，则有可能是16进制，转移至状态4
				word[i++] = q;
				state = 4;
				break;
			case op: // 成功识别为整数
				word[i] = '\0';
				printf("%s is an Integer.\n", word);
				result += "i";
				result += q;
				//cout << result << endl;
				memset(word, 0, sizeof word);
				i = 0;
				state = 0;
				break;
			default:
				word[i++] = q;
				state = 5;
			}
			break;
		case 3: // 3状态
			switch (isDigitOrChar(q)) {
			case op: // 识别为16进制数
				word[i] = '\0';
				printf("%s is a Hex digit.\n", word);
				result += "i";
				result += q;
				//cout << result << endl;
				memset(word, 0, sizeof word);
				i = 0;
				state = 0;
				break;
			default:
				word[i++] = q;
				state = 5;
			}
			break;
		case 4: // 4状态
			switch (isDigitOrChar(q)) {

			case digit: // 若为数字或A~F，仍为状态4，往下读入
			case AF:
				word[i++] = q;
				state = 4;
				break;
			case Hh:
				word[i++] = q;
				state = 3;
				break;
			case op: // 如果16进制没有以h或H结尾，转移至错误状态
				state = 5;
				cnt--;
				break;
			default:
				word[i++] = q;
				state = 5;
			}
			break;
		case 5: // 出错状态
			if (isDigitOrChar(q) == op) { // 若为空格，则识别为非标识符
				word[i] = '\0';
				printf("%s is not an identifier.\n", word);
				memset(word, 0, sizeof word);
				i = 0;
				state = 0;
				result = "-1";
				return result;
			}
			else { // 出错序列还未读取完毕，往下读入
				word[i++] = q;
				q = words[cnt++];
				continue;
			}
			break;
		}
		q = words[cnt++]; // 指针下移（指向输入符号串中的下一个字符）
	}

	return result;
}

// 判断是否是终结符
bool check_terminal(char ch) {
	if (isDigitOrChar(ch) == op || ch == 'i') return true;
	else return false;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388

五、实验结果（运行截屏）

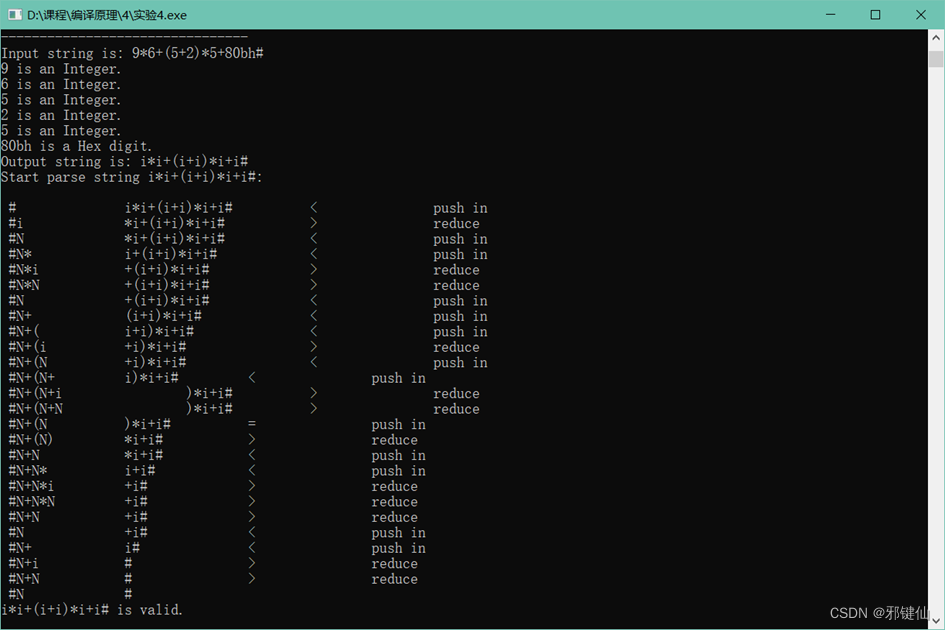
六、实验总结

（1）重点与难点
双向链表的使用不熟练，造成编写难度较大
规约时找最左边的大于关系的逻辑复杂，理解有点困难，花费很长时间

（2）存在的不足
算符优先表已在程序中给出，未实现代码分析文法，自主生成算符优先关系表的功能
输出的语法分析过程，对齐效果实现得不好

（3）未来改进方案
尝试编写算符优先关系的实现代码，扩大代码适用范围
封装一些重复代码，尽量减少代码冗余

（4）结论（开发体验、收获、感想等）
本次实验用到了数据结构中栈，双向链表的相关知识，通过实验，对这部分的基础知识进行了进一步的巩固。算符优先语法分析在理论课中是一个难点和重点，通过本次实验，我基本上理解了该语法的逻辑，巩固并加深了对这部分知识的理解与记忆。实验过程中，根据老师ppt提供的思路，将归约，移入等过程用switch函数分别进行实现。

七、测试用例

7+9*2#
80+5eH+(6+1)*2+4h#
95eah+3*(5+10)+35h#
9*6+(5+2)*5+80bh#
59h+((3+9ah)*3+4#
6+(5+2))*5+80bh#
1
2
3
4
5
6