前言

  本文重点是bitmap和布隆过滤器

  本专栏知识点是通过零声教育的线上课学习，进行梳理总结写下文章，对c/c++linux课程感兴趣的读者，可以点击链接 C/C++后台高级服务器课程介绍 详细查看课程的服务。

背景

• 在使⽤word⽂档时，word如何判断某个单词是否拼写正确？
• ⽹络爬⾍程序，怎么让它不去爬相同的url⻚⾯？允许有误差
• 垃圾邮件（短信）过滤算法如何设计？允许有误差
• 公安办案时，如何判断某嫌疑⼈是否在⽹逃名单中？控制误差 假阳率
• 缓存穿透问题如何解决？允许有误差

需求

  从海量数据中查询某字符串是否存在

红黑树

  不论是AVL还是红黑树，在“海量数据”数据面前都是不合适的，因为红黑树会将key，即数据存储起来，而海量的数据会导致内存不足。并且设计到字符串比较，效率也是很慢的。所以在这个需求下，用树相关的数据结构是不合适的。

  
拓展：

• c++标准库（STL）中的set和map结构都是采⽤红⿊树实现的，它增删改查的时间复杂度是$O(lo{g}_{2}N)$。set和map的关键区别是set不存储val字段
• 优点：存储效率⾼，访问速度⾼效
• 缺点：对于数据量⼤且查询字符串⽐较⻓且查询字符串相似时将会是噩梦

散列表hashtable

  散列表构成：数组+hash函数。它是将字符串通过hash函数⽣成⼀个整数再映射到数组当中(所以散列表不需要”比较字符串“，而红黑树需要)，它增删改查的时间复杂度是o(1)。

注意：散列表的节点中 kv 是存储在一起的

struct node {
	void *key;
	void *val;
	struct node *next;
};
1
2
3
4
5

  

拓展：

• c++标准库（STL）中的unordered_map<string, bool>是采⽤hashtable实现的
• hashtable中节点存储了key和val，hashtable并没有要求key的⼤⼩顺序，我们同样可以修改代码让插⼊存在的数据变成修改操作
• 优点：访问速度更快；不需要进⾏字符串⽐较
• 缺点：需要引⼊策略避免冲突，存储效率不⾼；空间换时间

hash函数

  
  hash函数的作⽤：避免插⼊的时候字符串的⽐较，hash函数计算出来的值通过对数组⻓度的取模能随机分布在数组当中。
  
  hash冲突（hash碰撞）：hash(key)=addr，hash 函数可能会把两个或两个以上的不同 key 映射到同一地址。hash函数⼀般返回的是64位整数，将多个⼤数映射到⼀个⼩数组中，必然会产⽣冲突。
  
  负载因子：用来形容散列表的存储密度。数组存储元素的个数 / 数据长度；负载因子越小，冲突越小，负载因子越大，冲突越大。
  
  

选择hash

如何选取hash函数？

1. 选取计算速度快
2. 强随机分布(等概率、均匀地分布在整个地址空间）

murmurhash1，murmurhash2，murmurhash3，siphash（redis6.0当中使⽤，rust等大多数语言选用的hash算法来实现hashmap），cityhash 都具备强随机分布性

测试地址如下：https://github.com/aappleby/smhasher

  siphash 主要解决字符串接近的强随机分布性,所以如果要hash字符串的话，优先选用siphash

冲突处理

• 链表法

  引用链表来处理哈希冲突，也就是将冲突元素用链表链接起来，这也是常用的处理冲突的⽅式。但是可能出现一种极端情况，冲突元素比较多，该冲突链表过长，这个时候可以将这个链表转换为红黑树。由原来链表时间复杂度 转换为红黑树时间复杂度 ，那么判断该链表过长的依据是多少？可以采⽤超过 256（经验值）个节点的时候将链表结构转换为红黑树结构。

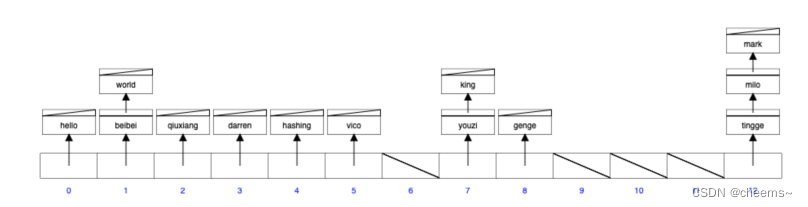
• 开放寻址法

  将所有的元素都存放在哈希表的数组中，不使用额外的数据结构；一般使用线性探查的思路解决

1. 当插⼊新元素的时，使⽤哈希函数在哈希表中定位元素位置
2. 检查数组中该槽位索引是否存在元素。如果该槽位为空，则插⼊，否则3
3. 在 2 检测的槽位索引上加⼀定步⻓接着检查2

加⼀定步⻓分为以下几种

1. i+1,i+2,i+3,i+4, … ,i+n
2. i-$1^2$ ,i+$2^2$ ,i- $3^2$,1+$4^2$ …

  这两种都会导致同类hash聚集，也就是近似值它的hash值也近似。那么它的数组槽位也靠近，形成hash聚集。第⼀种同类聚集冲突在前，第⼆种只是将聚集冲突延后。

3. 可以使⽤双重哈希来解决上⾯出现hash聚集现象

在.net HashTable类的hash函数Hk定义如下：

Hk(key) = [GetHash(key) + k * (1 + (((GetHash(key) >> 5) + 1) % (hashsize – 1)))] % hashsize

在此 (1 + (((GetHash(key) >> 5) + 1) % (hashsize – 1))) 与 hashsize 互为素数（两数互为素数表示两者没有共同的质因⼦）
执⾏了 hashsize 次探查后，哈希表中的每⼀个位置都有且只有⼀次被访问到，也就是说，对于给定的 key，对哈希表中的同⼀位置不会同时使⽤ Hi 和 Hj；
具体原理：https://www.cnblogs.com/organic/p/6283476.html

bitmap

  先来介绍bitmap，下面再引出布隆过滤器。现在有一个需求：文件中有40亿个QQ号码，请设计算法对QQ号码去重，相同的QQ号码仅保留一个，内存限制1G。

• 如果先排序再去重，时间复杂度太高
• 如果用hashmap天然去重，空间复杂度太高
• 文件切割避免内存过大，太麻烦，效率不高
• 使用bitmap，可以顺利地同时解决时间问题和空间问题

  一个unsigned int类型，共有32位，可以标识0 ~ 31这32个整数的存在与否。两个unsigned int类型，共有64位，可以标识0 ~ 63这64个整数的存在与否。

  那么如果我们把整个整数范围都覆盖了，这样一来1代表第一个位，2代表第二个位，2的32次方代表最后一个位。40亿个数中，存在的数就在相应的位置1，其他位就是0。比如来了一个1234，就找一下第1234位，如果是1就存在，是0就不存在。

   所以我们只要有足够的”位“，就可以判断0~4亿这4亿个整数是否存在了。2的32次是4,294,967,296。也就是说我们要有4,294,967,296个位。

   4,294,967,296个位=2的32次方个位=2的29次方个字节=512MB。原来32位的整数,转化成了1位的布尔，所以数据空间就是原来的32分之一。

  可以看到，使用bitmap不但自动去重，甚至这个需求我们还排了序，从小到大遍历正整数，当bitmap位的值为1时，就输出该值，输出后的正整数序列就是排序后的结果。

m%$2^n$ = m & ($2^n$-1) ------为了计算更高效，一般将 取模运算 变成 与运算

海量数据去重布隆过滤器

  红⿊树和hashtable都不能解决海量数据问题，它们都需要存储具体字符串，如果数据量⼤，提供不了⼏百G的内存；所以需要尝试探寻不存储key的⽅案，并且拥有hashtable的优点（不需要⽐较字符串）。而布隆过滤器就刚好满足这一需求，它不需要存储具体字符串，也不需要比较。时间和空间复杂度都低。

布隆过滤器介绍

布隆过滤器定义：布隆过滤器是⼀种概率型数据结构，它的特点是⾼效的插⼊和查询，能明确告知某个字符串⼀定不存在或者可能存在；

优缺点：布隆过滤器相⽐传统的查询结构（例如：hash，set，map等数据结构）更加⾼效，占⽤空间更⼩，但是确定是它返回的结果是概率性的，结果存在一定的误差，误差可控，同时不支持删除操作

构成：位图（bit数组）+ n个hash函数。

布隆过滤器原理

  当一个元素加入位图时：通过 K 个 hash 函数运算将这个元素映射到位图的 K 个点，并将它们置为1
  当检索一个元素时：通过通过 K 个 hash 函数运算检测位图的 K 个点是否都为1，如果都为1，则可能存在；如果有一个不为1，则一定不存在。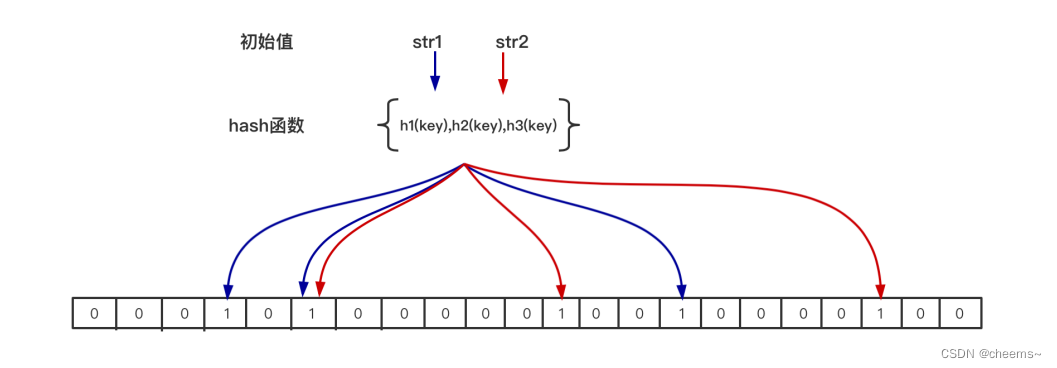

  为什么不支持删除操作？因为在位图中每个槽位只有两种状态（0 或者 1），一个槽位被设置为 1 状态，但不确定它被设置了多少次；也就是不知道被多少个 key 哈希映射而来以及是被具体哪个 hash 函数映射而来，所以不支持删除操作。

  如果想实现删除操作，可以用两个布隆过滤器，将删除的元素，放入第二个布隆过滤器里面，然后查询的时候去第二个里面查，如果第二个里面能查到说明可能被删除（注意也是存在误差的）。

布隆过滤如何应用

变量关系

  在实际应⽤过程中，布隆过滤器该如何使⽤？要选择多少个hash函数，要分配多少空间的位图，存储多少元素？另外如何控制假阳率（布隆过滤器能明确⼀定不存在，不能明确⼀定存在，那么存在的判断是有误差的，假阳率就是错误判断存在的概率）？

• n - - 布隆过滤器中元素的个数，如上图 只有str1和str2 两个元素 那么 n=2。预取存储多少个值
• p - - 假阳率，在0-1之间 0.0000001。能够接受的假阳率
• m - - 位图所占空间
• k - - hash函数的个数

公式如下：
n = ceil(m / (-k / log(1 - exp(log(p) / k))))
p = pow(1 - exp(-k / (m / n)), k)
m = ceil((n * log(p)) / log(1 / pow(2, log(2))))
k = round((m / n) * log(2))
1
2
3
4
5

确定n和p

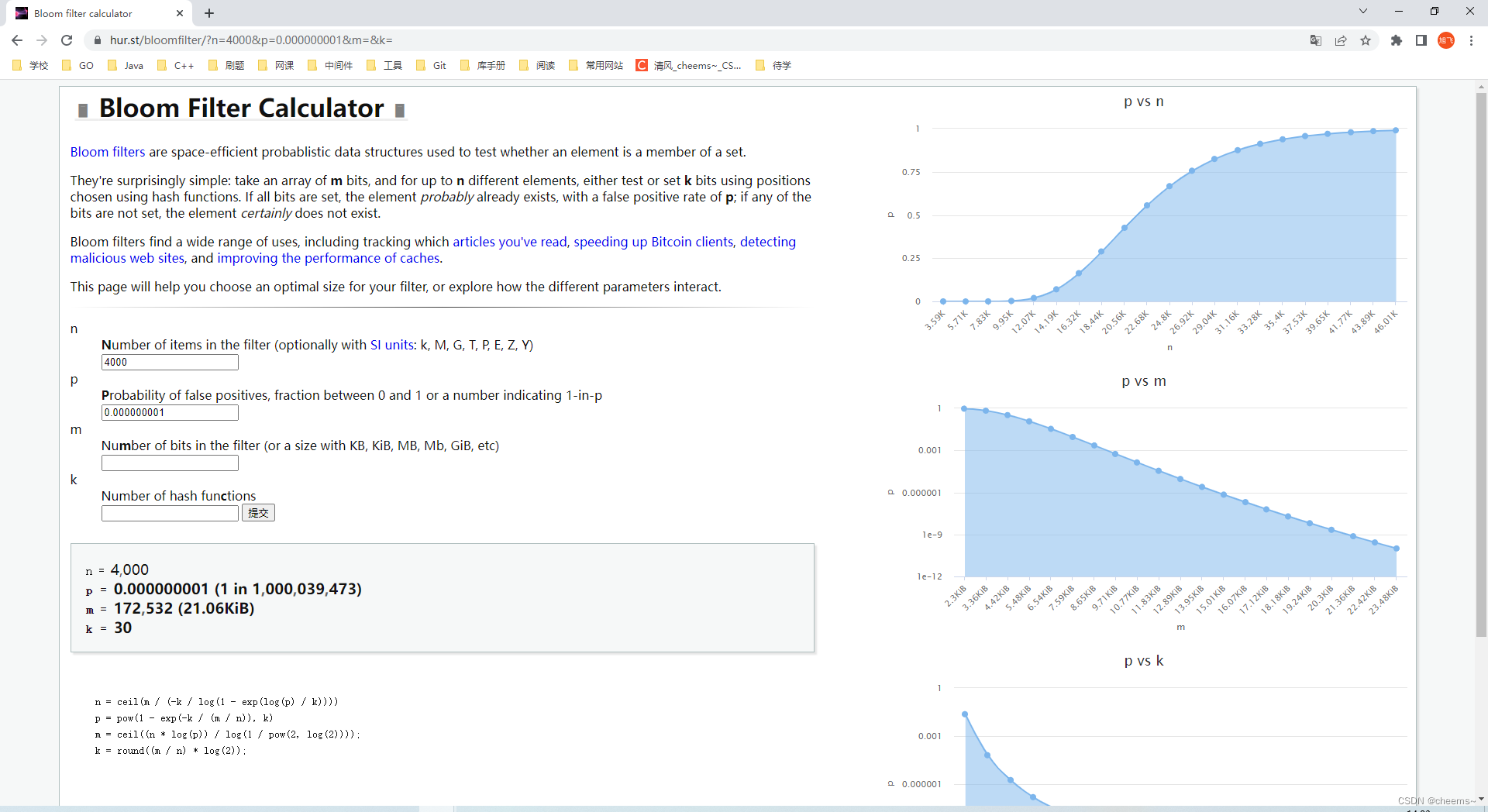
  在实际使用布隆过滤器时，首先需要确定 n 和 p，通过上面的运算得出 m 和 k；通常可以在下面这个网站上选出合适的值

https://hur.st/bloomfilter/
1

  现在假设n = 4000，p = 0.000000001。我们可以自己带入公式计算m和k，也可以带入网站计算得出变量值，并且右边缩略图可以观察不同值的情况。

n = 4000
p = 0.000000001 (1 in 1000039473)
m = 172532 (21.06KiB)
k = 30
1
2
3
4

选择k个hash函数

  我们发现上面计算出需要30个hash函数，难道我们要去找30个不同的hash函数来吗，显然不该这样。我们应该选择一个 hash 函数，通过给 hash 传递不同的种子偏移值，采用线性探寻的方式构造多个 hash函数。

// 采⽤⼀个hash函数，给hash传不同的种⼦偏移值
// #define MIX_UINT64(v) ((uint32_t)((v>>32)^(v)))
uint64_t hash1 = MurmurHash2_x64(key, len, Seed);
uint64_t hash2 = MurmurHash2_x64(key, len, MIX_UINT64(hash1));
// k 是hash函数的个数
for (i = 0; i < k; i++) {
   Pos[i] = (hash1 + i*hash2) % m; // m 是位图的⼤⼩
}
//通过这种⽅式来模拟 k 个hash函数 跟我们前⾯开放寻址法 双重hash是⼀样的思路
1
2
3
4
5
6
7
8
9

    
    

  题外话，面试百度：hash 函数实现过程当中 为什么 会出现 i * 31?

• i * 31 = i * (32-1) = i * (1<<5 -1) = i << 5 - i；
• 31 质数，hash 随机分布性很好

布隆过滤器应用场景

布隆过滤器通常用于判断某个 key 一定不存在的场景，同时允许判断存在时有误差的情况

常见处理场景：① 缓存穿透的解决；② 热 key 限流

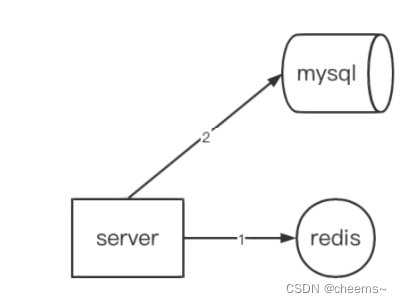
缓存场景：为了减轻数据库的访问压力，在server和mysql之间加入缓存来存储热点数据

缓存穿透：server请求数据时，缓存和数据库都没有该数据，最终导致压力全部给到数据库

读取步骤：

1. 先访问redis，如果存在则返回，不存在则 2
2. 访问mysql，如过不存在则返回，存在则 3
3. 将mysql的key写回redis

解决方案：

1. 在redis设置<key,null>以此避免访问mysql，但是如果<key,null>过多会占用内存（可以设置过期时间解决这一问题）
2. 在server端存储一个布隆过滤器，将mysql包含的key都放入布隆过滤器，布隆过滤器能过滤一定不存在的数据