前言

MATLAB进行图像处理相关的学习是非常友好的，可以从零开始，对基础的图像处理都已经有了封装好的许多可直接调用的函数，这个系列文章的话主要就是介绍一些大家在MATLAB中常用一些概念函数进行例程演示！

模拟退火算法（Simulate Anneal Arithmetic，SAA）是一种通用概率演算法，用来在一个大的搜寻空间内找寻命题的最优解。模拟退火是S.Kirkpatrick, C.D.Gelatt和M.P.Vecchi在1983年所发明。而V.Černý在1985年也独立发明此演算法。模拟退火算法是解决TSP问题的有效方法之一。

一.模拟退火基础

模拟退火来自冶金学的专有名词退火。退火是将材料加热后再经特定速率冷却，目的是增大晶粒的体积，并且减少晶格中的缺陷。材料中的原子原来会停留在使内能有局部最小值的位置，加热使能量变大，原子会离开原来位置，而随机在其他位置中移动。退火冷却时速度较慢，使得原子有较多可能可以找到内能比原先更低的位置。

模拟退火的原理也和金属退火的原理近似：将热力学的理论套用到统计学上，将搜寻空间内每一点想像成空气内的分子；分子的能量，就是它本身的动能；而搜寻空间内的每一点，也像空气分子一样带有“能量”，以表示该点对命题的合适程度。演算法先以搜寻空间内一个任意点作起始：每一步先选择一个“邻居”，然后再计算从现有位置到达“邻居”的概率。

模拟退火算法可以分解为解空间、目标函数和初始解三部分。

模拟退火的基本思想:

(1) 初始化：初始温度T(充分大)，初始解状态S(是算法迭代的起点)， 每个T值的迭代次数L；

(2) 对k=1，……，L做第(3)至第6步；

(3) 产生新解S′；

(4) 计算增量Δt′=C(S′)-C(S)，其中C(S)为评价函数；

(5) 若Δt′<0则接受S′作为新的当前解，否则以概率exp(-Δt′/T)接手S′作为新的当前解；

(6) 如果满足终止条件则输出当前解作为最优解，结束程序。终止条件通常取为连续若干个新解都没有被接受时终止算法；

(7) T逐渐减少，且T->0，然后转第2步；

模拟退火算法新解的产生和接受可分为如下四个步骤：

第一步：由一个产生函数从当前解产生一个位于解空间的新解；为便于后续的计算和接受，减少算法耗时，通常选择由当前新解经过简单地变换即可产生新解的方法，如对构成前解的全部或部分元素进行置换、互换等，注意到产生新解的变换方法决定了当前新解的邻域结构，因而对冷却进度表的选取有一定的影响。

第二步：计算与新解所对应的目标函数差。因为目标函数差仅由变换部分产生，所以目标函数差的计算最好按增量计算。事实表明，对大多数应用而言，这是计算目标函数差的最快方法。

第三步：判断新解是否被接受，判断的依据是一个接受准则，最常用的接受准则是Metropolis准则: 若Δt′<0则接受S′作为新的当前解S，否则以概率exp(-Δt′/T)接受S′作为新的当前解S。

第四步：当新解被确定接受时，用新解代替当前解，这只需将当前解中对应于产生新解时的变换部分予以实现，同时修正目标函数值即可。此时，当前解实现了一次迭代。可在此基础上开始下一轮试验。而当新解被判定为舍弃时，则在原当前解的基础上继续下一轮试验。

搜寻资料的时候遇到的这个示例，这里分享给大家，MATLAB版本为MATLAB2015b。

二. MATLAB仿真一

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
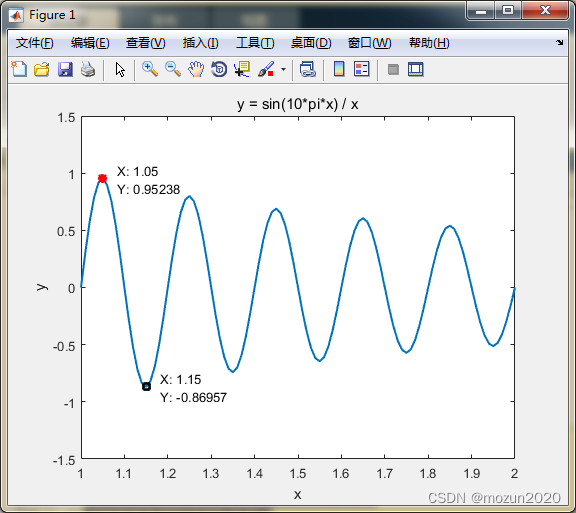
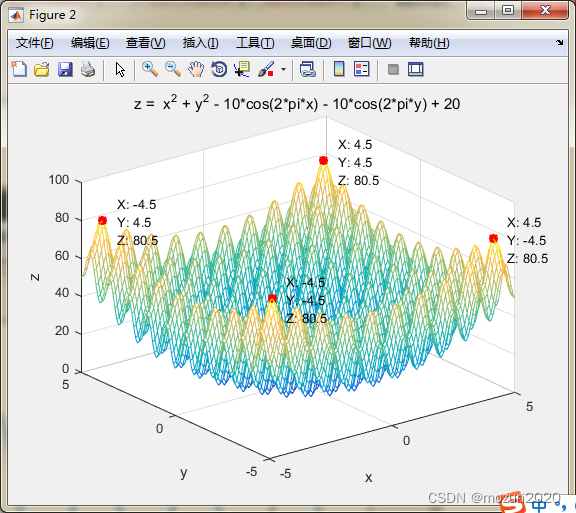
%功能：矩阵分析--模拟退火
%环境：Win7，Matlab2015b
%Modi: C.S
%时间：2022-06-27
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%


%% I. 清空环境变量
clear all
clc

tic
%% II. 一元函数优化
x = 1:0.01:2;
y = sin(10*pi*x) ./ x;
figure
plot(x,y,'linewidth',1.5)
ylim([-1.5, 1.5])
xlabel('x')
ylabel('y')
title('y = sin(10*pi*x) / x')
hold on

%%
% 1. 标记出最大值点
[maxVal,maxIndex] = max(y);
plot(x(maxIndex), maxVal, 'r*','linewidth',2)
text(x(maxIndex), maxVal, {['    X: ' num2str(x(maxIndex))];['    Y: ' num2str(maxVal)]})
hold on

%%
% 2. 标记出最小值点
[minVal,minIndex] = min(y);
plot(x(minIndex), minVal, 'ks','linewidth',2)
text(x(minIndex), minVal, {['    X: ' num2str(x(minIndex))];['    Y: ' num2str(minVal)]})

%% III. 二元函数优化
[x,y] = meshgrid(-5:0.1:5,-5:0.1:5);
z = x.^2 + y.^2 - 10*cos(2*pi*x) - 10*cos(2*pi*y) + 20;
figure
mesh(x,y,z)
hold on
xlabel('x')
ylabel('y')
zlabel('z')
title('z =  x^2 + y^2 - 10*cos(2*pi*x) - 10*cos(2*pi*y) + 20')

%%
% 1. 标记出最大值点
maxVal = max(z(:));
[maxIndexX,maxIndexY] = find(z == maxVal);
for i = 1:length(maxIndexX)
    plot3(x(maxIndexX(i),maxIndexY(i)),y(maxIndexX(i),maxIndexY(i)), maxVal, 'r*','linewidth',2)
     text(x(maxIndexX(i),maxIndexY(i)),y(maxIndexX(i),maxIndexY(i)), maxVal, {['    X: ' num2str(x(maxIndexX(i),maxIndexY(i)))];['    Y: ' num2str(y(maxIndexX(i),maxIndexY(i)))];['    Z: ' num2str(maxVal)]})
    hold on
end
toc
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

点击“运行”，得到如下结果：

三. MATLAB仿真二

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
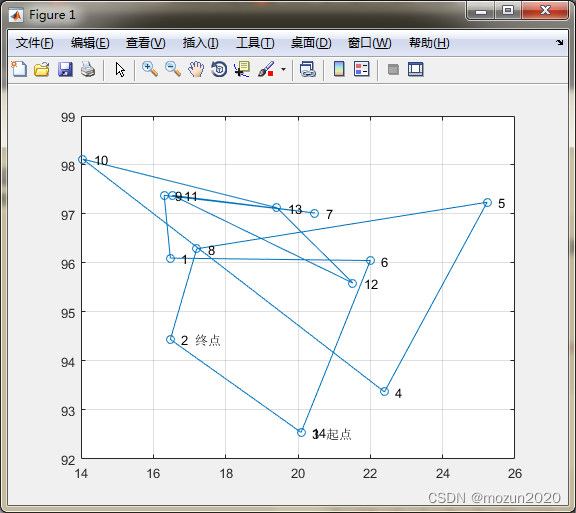
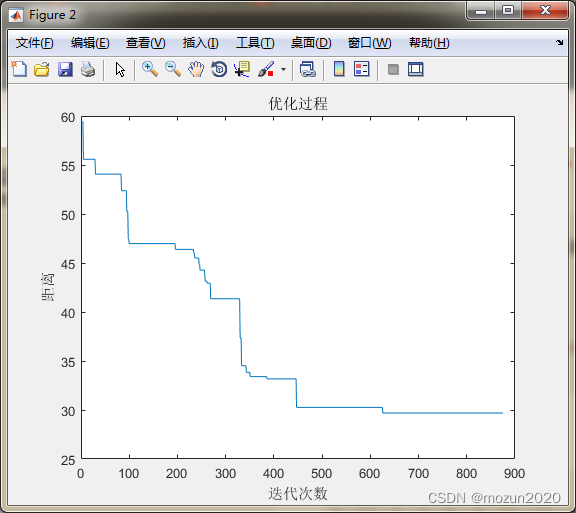
%功能：矩阵分析--模拟退火
%环境：Win7，Matlab2015b
%Modi: C.S
%时间：2022-06-27
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%% I. 清空环境变量
clear all
clc

tic
%% II. 导入城市位置数据
X = [16.4700   96.1000
     16.4700   94.4400
     20.0900   92.5400
     22.3900   93.3700
     25.2300   97.2400
     22.0000   96.0500
     20.4700   97.0200
     17.2000   96.2900
     16.3000   97.3800
     14.0500   98.1200
     16.5300   97.3800
     21.5200   95.5900
     19.4100   97.1300
     20.0900   92.5500];

%% III. 计算距离矩阵
D = Distance(X);  %计算距离矩阵
N = size(D,1);    %城市的个数

%% IV. 初始化参数
T0 = 1e10;   % 初始温度
Tend = 1e-30;  % 终止温度
L = 2;    % 各温度下的迭代次数
q = 0.9;    %降温速率
Time = ceil(double(solve([num2str(T0) '*(0.9)^x = ',num2str(Tend)])));  % 计算迭代的次数
% Time = 132;
count = 0;        %迭代计数
Obj = zeros(Time,1);         %目标值矩阵初始化
track = zeros(Time,N);       %每代的最优路线矩阵初始化

%% V. 随机产生一个初始路线
S1 = randperm(N);
DrawPath(S1,X)
disp('初始种群中的一个随机值:')
OutputPath(S1);
Rlength = PathLength(D,S1);
disp(['总距离：',num2str(Rlength)]);

%% VI. 迭代优化
while T0 > Tend
    count = count + 1;     %更新迭代次数
    temp = zeros(L,N+1);
    %%
    % 1. 产生新解
    S2 = NewAnswer(S1);
    %%
    % 2. Metropolis法则判断是否接受新解
    [S1,R] = Metropolis(S1,S2,D,T0);  %Metropolis 抽样算法
    %%
    % 3. 记录每次迭代过程的最优路线
    if count == 1 || R < Obj(count-1)
        Obj(count) = R;           %如果当前温度下最优路程小于上一路程则记录当前路程
    else
        Obj(count) = Obj(count-1);%如果当前温度下最优路程大于上一路程则记录上一路程
    end
    track(count,:) = S1;
    T0 = q * T0;     %降温
end

%% VII. 优化过程迭代图
figure
plot(1:count,Obj)
xlabel('迭代次数')
ylabel('距离')
title('优化过程')

%% VIII. 绘制最优路径图
DrawPath(track(end,:),X)

%% IX. 输出最优解的路线和总距离
disp('最优解:')
S = track(end,:);
p = OutputPath(S);
disp(['总距离：',num2str(PathLength(D,S))]);
toc
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88

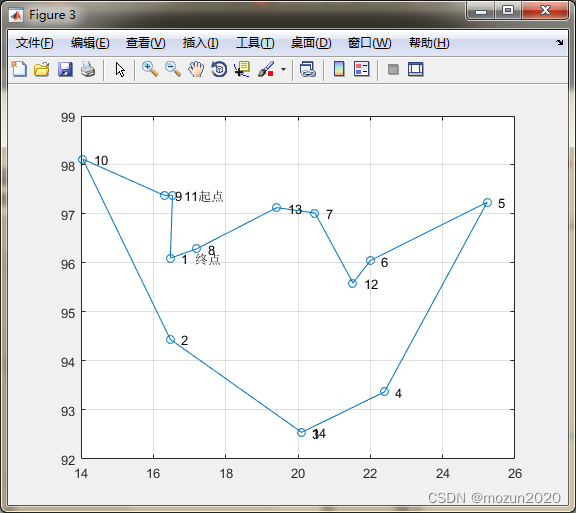
点击“运行”，得到如下结果：

初始种群中的一个随机值:
3—>14—>6—>1—>9—>7—>11—>12—>13—>10—>4—>5—>8—>2—>3
总距离：60.8861
最优解:
11—>9—>10—>2—>14—>3—>4—>5—>6—>12—>7—>13—>8—>1—>11
总距离：29.6889
时间已过 1.465166 秒。
1
2
3
4
5
6
7

四. 小结

模拟退火算法的应用很广泛，可以较高的效率求解最大截问题(Max Cut Problem)、0-1背包问题(Zero One Knapsack Problem)、图着色问题(Graph Colouring Problem)、调度问题(Scheduling Problem)等等。这个示例，后期可能会用到，做个笔记。每天学一个MATLAB小知识，大家一起来学习进步阿！