1. 什么是二叉搜索树

二叉搜索树又称二叉排序树，它是一棵空树 或者 具有以下性质的二叉树：

1. 若它的左子树不为空，则它左子树上的所有的结点的值都小于根结点的值
2. 若它的右子树不为空，则它的右子树上的所有结点的值都大于根结点的值
3. 它的左右也都为二叉搜索树

例如：

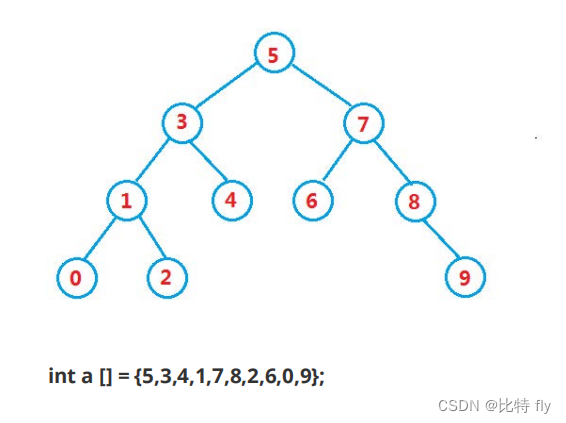
2. 二叉搜索树的操作

2.1 查找

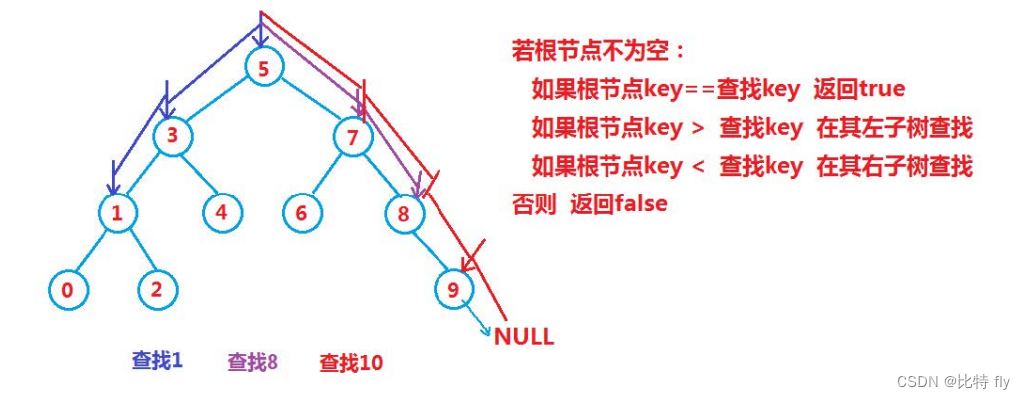
2.2 插入

1. 如果为空树，即 root==null ，就直接插入即可
2. 如果不为空树，就根据搜索二叉树的性质进行插入，即寻找合适的插入位置，思路和查找思路一样

注意：插入的位置一定是搜索二叉树的根节点

2.3 删除

设待删除的结点为 cur ，待删除结点的双亲结点为 parent

1. 如果 cur.left == null :

1. 如果 cur == root，则root == cur.right
2. 如果 cur != root，cur 是parent的左子树，则parent.left == cur.right
3. 如果 cur != root，cur 是parent的右子树，则parent.right == cur.right
   

2. 如果 cur.right == null :

1. 如果 cur == root，则root == cur.left
2. 如果 cur != root，cur 是parent的左子树，则parent.left == cur.left
3. 如果 cur != root，cur 是parent的右子树，则parent.right == cur.left
   

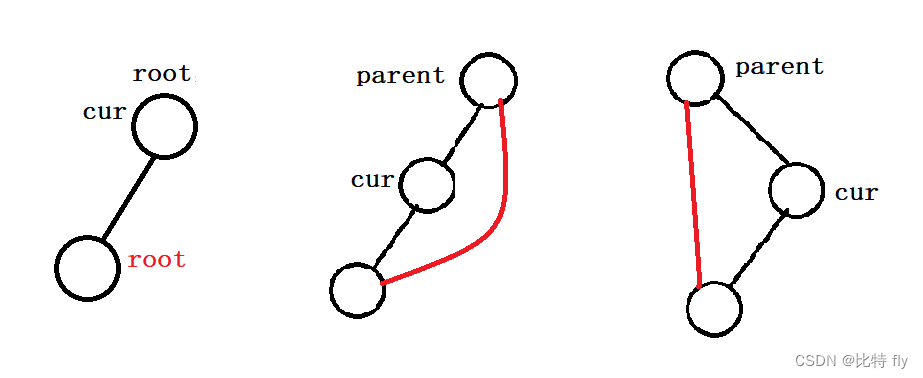
3. cur.left != null && cur.right != null :

需要使用替换法进行删除，用 cur 左子树中的最大值，或者 cur 右子树中的最小值替换掉删除结点，然后删除替换元素。
在找到replace并且替换cur之后，就可以进行如下操作（采用右树找最小值的方法）：

1. 如果 replace==cur.right ，则 cur.right = replace.right
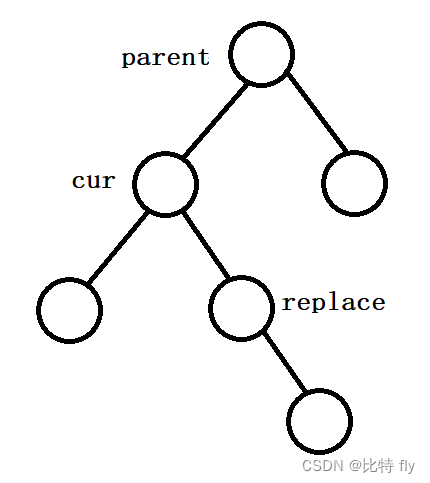
2. 如果 replace==cur.right ，则 replace_parent.left = replace.right
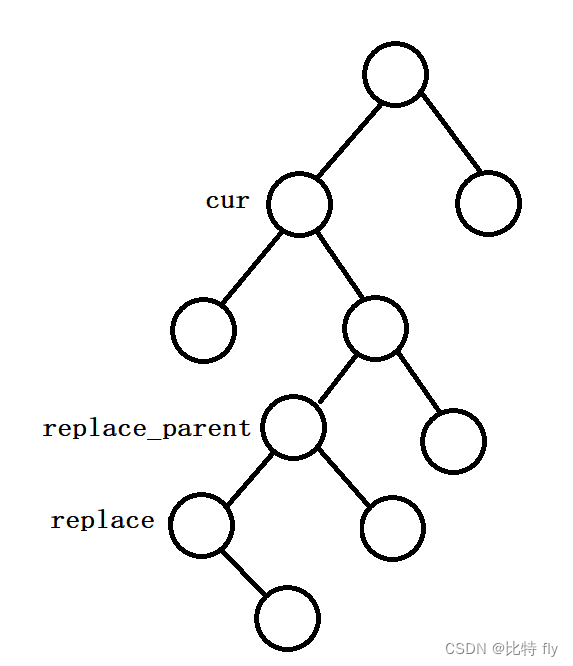
3. 注意：
   （1）在左子树找最大值时，这个值一定在左子树的最右边，而最右边的这个结点一定没有右子树；
   （2）在右子树中找最小值时，这个值一定在右子树最左边。而最左边的这个1结点一定没有左子树；

2.4 代码实现

BinarySearchTree：

public class BinarySearchTree {
    public static class Node{
        int val;
        Node left;
        Node right;
        public Node(int val){
            this.val=val;
        }
    }
    Node root;
    //查找
    public boolean search(int key){
        if(root==null){
            return false;
        }
        Node cur = root;
        while(cur!=null){
            if(cur.val==key){
                return true;
            }else if(key<cur.val){
                cur=cur.left;
            }else{
                cur=cur.right;
            }
        }
        return false;
    }

    //插入
    public void insert(int val){
        Node node = new Node(val);
        if(root==null){
            root=node;
        }else{
            Node parent = null;
            Node cur = root;
            while(cur!=null){
                if(val<cur.val){
                    parent=cur;
                    cur=cur.left;
                }else{
                    parent=cur;
                    cur=cur.right;
                }
            }
            if(val<parent.val){
                parent.left=node;
            }else{
                parent.right=node;
            }
        }
    }
    //删除
    private void delete_child(Node parent,Node cur){
        if(cur.left==null){
            if(cur==root){
                root=cur.right;
            }else{
                if(cur==parent.left){
                    parent.left=cur.right;
                }else{
                    parent.right=cur.right;
                }
            }
        }else if(cur.right==null){
            if(cur==root){
                root=cur.left;
            }else{
                if(cur==parent.left){
                    parent.left=cur.left;
                }else{
                    parent.right=cur.left;
                }
            }
        }else{
            Node replace = cur.right;
            Node replace_parent=parent;
            while(replace.left!=null){
                replace_parent=replace;
                replace=replace.left;
            }
            cur.val=replace.val;
            if(replace==cur.right){
                replace_parent.right=replace.right;
            }else{
                replace_parent.left=replace.right;
            }
        }
    }
    public boolean delete(int key){
        if(root==null){
            return false;
        }
        //找到要删除的结点
        Node cur = root;
        Node parent = null;
        while(cur!=null){
            if(cur.val==key){
                delete_child(parent,cur);
                return true;
            }else if(key<cur.val){
                parent=cur;
                cur=cur.left;
            }else{
                parent=cur;
                cur=cur.right;
            }
        }
        return false;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112

Test：

public class Test {
    public static void main(String[] args) {
        BinarySearchTree BST = new BinarySearchTree();
        int []arr = {5,3,4,1,7,8,2,6,0,9};
        for(int val:arr){
            BST.insert(val);
        }
        boolean ret1 = BST.search(0);
        boolean ret2 = BST.delete(5);
    }
}
1
2
3
4
5
6
7
8
9
10
11