数据结构的一些算法

数据结构

数据结构是相互之间存在一种或多种特定关系的数据元素的集合。
三要素：逻辑结构、存储结构和数据的运算。主要讲的时逻辑结构，下面会分别说明各结构。
在这里插入图片描述

线性结构链接

线性结构	特征	应用
栈	后进先出	表达式求值；递归中
队列	先进先出	层次遍历；计算机系统中应用
串		模式匹配算法-KMP
数组		存储特殊矩阵：对称矩阵、三角矩阵、稀疏矩阵（十字链表法）

树形结构链接

二叉树，先序遍历(PreOrder)、中序遍历(InOrder)、后序遍历(PostOrder)、层次遍历;
线索二叉树，为方便找到直接前驱和后继，内容有线索二叉树构造、遍历、找前驱和找后继；

树，孩子兄弟表示法、双亲表示法和孩子表示法，应用：哈夫曼编码
先根遍历 $\Leftrightarrow$ 二叉树先序遍历
后根遍历 $\Leftrightarrow$ 二叉树中序遍历

图状结构链接

图存储：邻接矩阵、邻接表、十字链表（有向图）、邻接多重表（无向图）
图的遍历：广度优先搜索 （BFS），深度优先搜索 （DFS）

图的应用：
最小生成树 【Prim（普里姆）、Kruskal（克鲁斯卡尔）】
最短路径 【Dijkstra（迪杰斯特拉）、Floyd（弗洛伊德）】
拓扑排序（AOV网）
关键路径

查找算法

因为文章篇幅太长了，把查找和排序也加个链接，这里就简单说下是个什么东西
查找算法链接（相同）
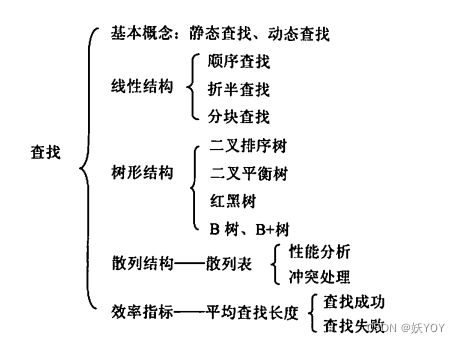
在这里插入图片描述

顺序查找法

思想：从头到尾挨个找（反过来也行）
顺序查找时间复杂度： $O (n)$

在这里插入图片描述

折半查找法

又称“二分查找”，仅适用于有序的顺序表
折半查找时间复杂度＝ $O(\log_2n)$

在这里插入图片描述

分块查找法

思想：
索引表中记录每个分块的最大关键字、分块的区间；
先查索引表（顺序或折半），再对分块内进行顺序查找.
块内无序，块间有序
在这里插入图片描述

设索引查找和块内查找的平均查找长度分别为 $L_1$ 、 $L_s$ ,则分块查找的平均查找长度为 $ASL=L_1 + L_s$
$\frac{s^2+2s+n}{2s}，当s=\sqrt n时，ALS_{最小}=\sqrt{n}+1$

在这里插入图片描述

树形查找法

n个结点的二叉树最小高度为 $\lfloor{\log_2n}\rfloor + 1$ 或是 $\lceil{\log_2(n+1)}\rceil$
对具有n个关键字的树型结构，具有n+1个叶结点

二叉排序树，BST

左子树节点值 $\leq$ 根节点值 $\leq$ 右子树结点值

查找思路：
若树非空，目标值与节点的值比较：
若相等，则查找成功；
若小于根节点，则在左子树上查找，否则在右子树上查找；
查找成功返回节点指针，失败返回NULL

在这里插入图片描述

平衡二叉排序树，AVL

AVL Tree链接
$\lvert 左子树高 -右子树高 \rvert \leq 1$ ，平衡因子只可取-1、0或1。
平衡二叉树平均查找长度为 $O(\log_2n)$

平衡二叉树

红黑树，RBT

Red/Black Tree链接

简要特点：
左右跟，根叶黑
不红红，黑路同

查找时间复杂度： $O(\log_2n)$

插入步骤
这张图笑死我了

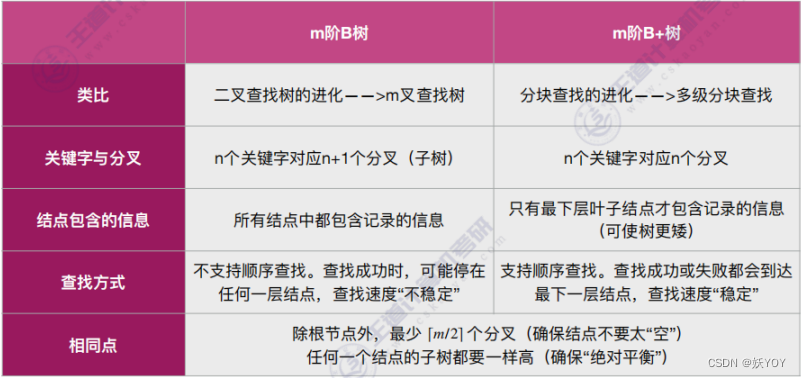
B树

B-Tree 链接

B树结构：

令 $k=\lceil{m/2}\rceil$
$\cdot k^{h-1}-1$
高度为h的3阶B树，含有关键字个数至少是： $2^h-1$ ，同完全二叉树（满二叉）
高度为h的5阶B树，含有关键字个数至少是： $\cdot 3^{h-1}-1$
高度为h的完全二叉树至少 $2^{h-1}$ 个结点，最多 $2^{h}-1$ 个结点

B+树

在这里插入图片描述

散列表（哈希表）

在这里插入图片描述

装填因子 $\alpha$ 越大，平均查找长度变大，“冲突”越多，查找效率越低

处理冲突方法

拉链法，下图：
开放定址法，下图：
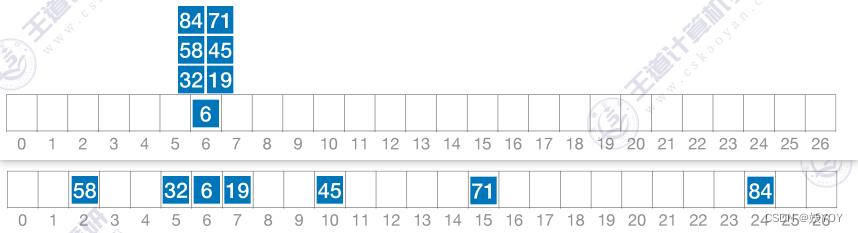
- ①线性探测法： $d_i=0,1,2,3,\cdots,m-1$ ，发生冲突，紧挨着往后移
- ②平方探测法，当 $d_i=0^2, 1^2, -1^2, 2^2, -2^2, \cdots , k^2, -k^2$ ，其中 $\leq m/2$ 。比起线性探测法更不容易产生“聚集（堆积）”问题。
- ③伪随机序列法， $d_i$ 是一个伪随机序列，自己定义的，如 $\ldots$
- ④再散列法（再哈希法）：除了原始的散列函数 $H (k e y)$ 之外，多准备几个散列函数，当散列函数冲突时，用下一个散列函数计算一个新地址，直到不冲突为止。

排序

排序算法链接
就看上面这个链接！
在这里插入图片描述

排序算法	平均时间复杂度	空间复杂度	稳定性
直接插入排序	$O(n^2)$	$O (1)$	稳定
折半插入排序	$O(n^2)$	$O (1)$	稳定
希尔排序	不确定，与增量d选择有关，比插入排序好	$O (1)$ ，仅顺序表	不稳定
冒泡排序	$O(n^2)$	$O (1)$	稳定
快速排序	$O(n\log_2n)$ ，划分平均最快，有序或逆序最慢 $O(n^2)$	平均 $O(\log_2n)$ ，最好： $O(\log_2n)$ ，最坏： $O (n)$	不稳定
简单选择排序	$O(n^2)$ ，与序列初始状态无关	$O (1)$	不稳定
堆排序	$O(n\log_2n)$	$O (1)$	不稳定
归并排序	$O(n\log_2n)$ ，与序列初始状态无关	$O (n)$	稳定
基数排序	$O (d (n + r))$ ，与初始序列次序无关	$O (r)$ ，一般用队列	稳定