开闭环系统性能分析（稳定性、收敛性、可控性）

一、传递函数的极点就是系统矩阵A的特征值

1. 系统传递函数的极点就是系统矩阵A的特征值

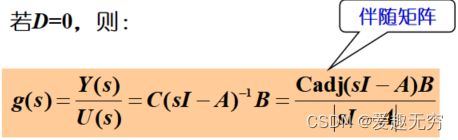
结论：
1、系统矩阵A的特征多项式等同于传递函数g(s)的分母多项式。
2、传递函数的极点就是系统矩阵A的特征值，与输入输出矩阵B，C无关。
3、同一系统的状态空间描述不惟一，但传递函数g(s)是惟一的，称为传递函数的不变性。

2. 稳定性和收敛性

某二阶线性时不变系统（LTI）模型：



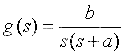
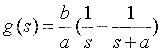
拉氏反变换得时域微分方程:

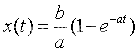
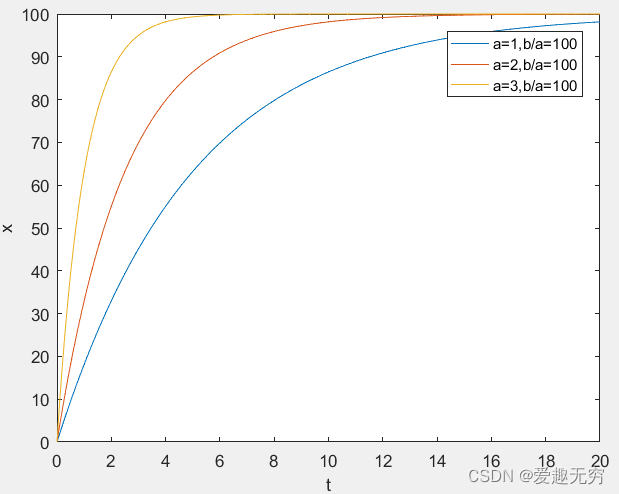
可见a越大，系统收敛得越快。

二、开闭环系统稳定性和收敛性

Open loop（开环系统）

开环系统矩阵A的特征值决定系统稳定性，收敛速度。
Close loop（闭环系统）

闭环系统的状态（空间）矩阵(Acl)，通过选取k的值，使得新的矩阵Acl的特征值在一个希望的位置上，从而改变稳定性，收敛速度。