-
矩阵分析与应用+张贤达
第一章 矩阵与线性方程组(十二)
1.函数向量的内积与范数
若 x ( t ) x(t) x(t)和 y ( t ) y(t) y(t)分别是变量 t t t的函数向量,则它们的内积定义为
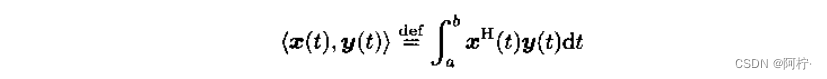
其中,变量t在[a,b]取值,且a<b。变量t可以是时间变量、频率变量或者空间变量。
两个函数向量的夹角定义为
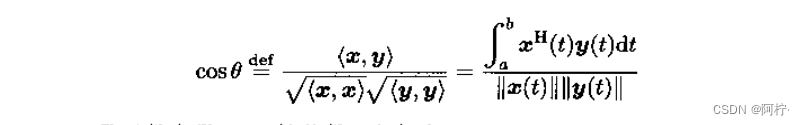
式中, ∣ ∣ x ( t ) ∣ ∣ ||x(t)|| ∣∣x(t)∣∣是函数向量 x ( t ) x(t) x(t)的范数,定义为
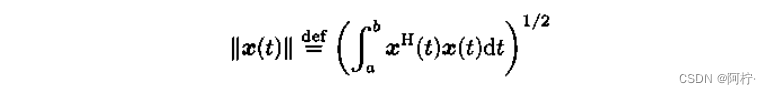
显然,若两个函数向量的内积等于零,即
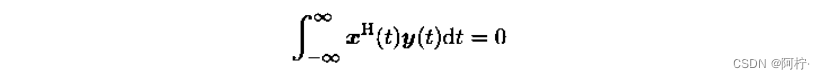
则 θ = π / 2 θ=π/2 θ=π/2。此时,称两个函数向量正交,并记作 x ( t ) ⊥ y ( t ) x(t) \bot y(t) x(t)⊥y(t)。2.随机向量的内积与范数
若 x ( ξ ) x(ξ) x(ξ)和 y ( ξ ) y(ξ) y(ξ)分别是样本变量ξ的随机向量,则它们的内积定义为
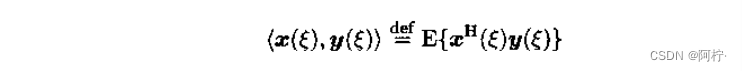
其中,样本变量 ξ ξ ξ可以是时间t、圆频率f、角频率w和空间变量s等。
随机向量 x ( ξ ) x(ξ) x(ξ)的范数定义为
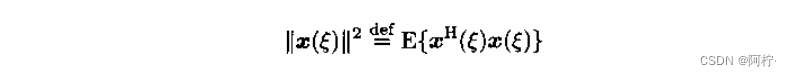
与常数向量和函数向量的情况不同,mx1随机向量 x ( ξ ) x(ξ) x(ξ)和nx1随机向量 y ( ξ ) y(ξ) y(ξ)称为正交
若 x ( ξ ) x(ξ) x(ξ)的任意元素与 y ( ξ ) y(ξ) y(ξ)的任意元素正交。这意味着,两个向量的互相关矩阵为零矩阵 O m x n O_{mxn} Omxn,即
E x ( ξ ) у H ( ξ ) = O m x n E{x(ξ)у^H(ξ)} = O_{mxn} Ex(ξ)уH(ξ)=Omxn
并记作 x ( ξ ) ⊥ y ( ξ ) x(ξ) \bot y(ξ) x(ξ)⊥y(ξ)。- 任意两个正交向量之和的范数平方等于各个向量范数平方之和。
命题 若 x ⊥ y x \bot y x⊥y,则 ∣ ∣ x + y ∣ ∣ 2 = ∣ ∣ x ∣ ∣ 2 + ∣ ∣ y ∣ ∣ 2 ||x+y||^2=||x||^2+||y||^2 ∣∣x+y∣∣2=∣∣x∣∣2+∣∣y∣∣2。
证明 由范数公理知
∣ ∣ x + y ∣ ∣ 2 = < x + y , x + y > = < x , x > + < x , y > + < y , x > + < y , y > ||x+y||^2=<x+y,x+y>=<x,x>+<x,y>+<y,x>+<y,y> ∣∣x+y∣∣2=<x+y,x+y>=<x,x>+<x,y>+<y,x>+<y,y>
由于 x x x和 y y y正交,所以 < x , y > = E x T y = 0 <x,y>=E{x^Ty}=0 <x,y>=ExTy=0。又由内积公理知 < y , x > = < x , y > = 0 <y,x>=<x,y>=0 <y,x>=<x,y>=0。
将这一结果代入上式得
∣ ∣ x + у ∣ ∣ 2 = < x , x > + < y , y > = ∣ ∣ x ∣ ∣ 2 + ∣ ∣ y ∣ ∣ 2 ||x+ у||^2 = <x,x> + <y,y> = ||x||^2 +||y||^2 ∣∣x+у∣∣2=<x,x>+<y,y>=∣∣x∣∣2+∣∣y∣∣2
命题得证。
这一命题也称Pythagorean定理。
命题 ∣ < x , y > ∣ ≤ ∣ ∣ x ∣ ∣ ∣ ∣ y ∣ ∣ |<x,y>|≤||x|| ||y|| ∣<x,y>∣≤∣∣x∣∣∣∣y∣∣,等号成立当且仅当 x = λ y x=λy x=λy或 x = 0 x=0 x=0或 y = 0 y=0 y=0.
证明 由内积的非负性知 < x − λ y , x − λ y > ≥ 0 <x-λy,x-λy>≥0 <x−λy,x−λy>≥0,其中, λ ≠ 0 λ≠0 λ=0为一标量。注意到
( x − λ y , x − λ y ) = < x , x > − λ < y , x > − λ < x , y > + λ 2 < y , y > (x-λy,x-λy)=<x,x>-λ<y,x>-λ<x,y>+λ^2<y,y> (x−λy,x−λy)=<x,x>−λ<y,x>−λ<x,y>+λ2<y,y>
选择 λ = < x , y > / ∣ ∣ y ∣ ∣ 2 λ=<x,y>/||y||^2 λ=<x,y>/∣∣y∣∣2,则上式变为
< x − λ y , x − λ y > = < x , x > − ∣ < x , x > 2 / ∣ ∣ y ∣ ∣ 2 = < x , x > − ∣ < x , y > ∣ 2 / < y , y > ≥ 0 <x-λy,x-λy>=<x,x>-|<x,x>^2/||y||^2=<x,x>-|<x,y>|^2/<y,y>≥ 0 <x−λy,x−λy>=<x,x>−∣<x,x>2/∣∣y∣∣2=<x,x>−∣<x,y>∣2/<y,y>≥0
由此得 ∣ < x , y > ≤ ∣ ∣ x ∣ ∣ ∣ ∣ y ∣ ∣ |<x,y>≤||x|| ||y|| ∣<x,y>≤∣∣x∣∣∣∣y∣∣。
显然,当 x = λ y x=λy x=λy或 x = 0 x=0 x=0或 y = 0 y=0 y=0时,不等式取等号。
不等式 ∣ < x , y > ∣ ≤ ∣ ∣ x ∣ ∣ ∣ ∣ y ∣ ∣ |<x,y>|≤||x|| ||y|| ∣<x,y>∣≤∣∣x∣∣∣∣y∣∣称为Cauchy-Schwartz不等式。命题 ∣ ∣ x + y ∣ ∣ 2 + ∣ ∣ x − y ∣ ∣ 2 = 2 ∣ ∣ x ∣ ∣ 2 + 2 ∣ ∣ y ∣ ∣ 2 ||x+y||^2+||x-y||^2=2||x||^2+2||y||^2 ∣∣x+y∣∣2+∣∣x−y∣∣2=2∣∣x∣∣2+2∣∣y∣∣2称为平行四边形法则。
证明 具体计算范数,得
∣ ∣ x + y ∣ ∣ 2 = < x + y , x + y > = < x , x > + 2 < x , y > + < y , y > ||x+y||^2=<x+y,x+y>=<x,x>+2<x,y>+<y,y> ∣∣x+y∣∣2=<x+y,x+y>=<x,x>+2<x,y>+<y,y>
∣ ∣ x − y ∣ ∣ 2 = < x − y , x + y > = < x , x > − 2 < x , y ) + < y , y > ||x-y||^2=<x-y,x+y>=<x,x>-2<x,y)+<y,y> ∣∣x−y∣∣2=<x−y,x+y>=<x,x>−2<x,y)+<y,y>
两式相加,即有
∣ ∣ x + y ∣ ∣ 2 + ∣ ∣ x − y ∣ ∣ 2 = 2 < x , x > + 2 < y , y > = 2 ( ∣ ∣ x ∣ ∣ 2 + ∣ ∣ y ∣ ∣ 2 ) ||x + y||^2 + ||x -y||^2= 2<x,x>+2<y,y>=2(||x||^2+ ||y||^2) ∣∣x+y∣∣2+∣∣x−y∣∣2=2<x,x>+2<y,y>=2(∣∣x∣∣2+∣∣y∣∣2)- 若
n
→
∞
n→∞
n→∞时,有
∣
∣
x
n
−
x
∣
∣
→
0
||x_n-x||→0
∣∣xn−x∣∣→0,则称
x
n
x_n
xn收敛为
x
x
x.
下面的命题表明,范数具有连续性。
命题 若 x n → x x_n→x xn→x和 y n → y y_n→y yn→y,则 < x n , y n > → < x , y > <x_n,y_n>→<x,y> <xn,yn>→<x,y>。
证明 若 x n → x x_n→x xn→x和 y n → y y_n→y yn→y,则 x n x_n xn和 y n y_n yn必然是有界的向量,即 ∣ ∣ x n ∣ ∣ ≤ m 1 ||x_n||≤m_1 ∣∣xn∣∣≤m1和 ∣ ∣ y n ∣ ∣ ≤ m 2 ∣ ∣ , 且 ||y_n||≤m_2||,且 ∣∣yn∣∣≤m2∣∣,且||x_n-x||→0,||y_n-y||→0&当 n → ∞ n→∞ n→∞。
考查
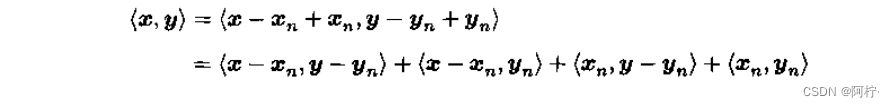
然而,上式右边前三项分别为
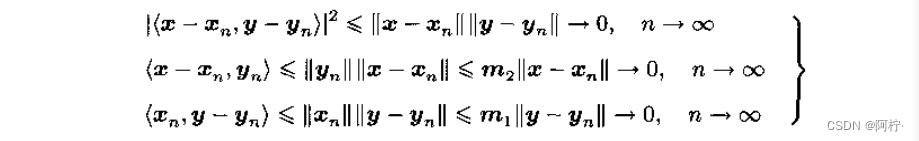
将以上公式代入即知:当 n → ∞ n→∞ n→∞时, < x n , y n > → < x , y > <x_n,y_n>→<x,y> <xn,yn>→<x,y>。
3.对常数向量、函数向量和随机向量的正交的归纳与总结
(1)数学定义:两个向量x和y正交,若它们的内积等于零,即 < x , y > = 0 <x,y>=0 <x,y>=0(对常数向量和函数向量),或者它们的外积的数学期望等于零矩阵,即 E x y H = 0 E{xy^H}=0 ExyH=0(对随机向量)。
(2)几何解释:若两个向量正交,则这两个向量之间的夹角为90,并且一个向量到另一个向量的投影等于零。
(3)物理意义:当两个向量正交时,一个向量中将不含另一个向量的任何成分,即这两个向量之间不存在任何相互作用或干扰。 - 任意两个正交向量之和的范数平方等于各个向量范数平方之和。
-
相关阅读:
Azure Virtual Desktop(一)创建配置管理
基于蝙蝠算法的无人机航迹规划-附代码
由两个独立的高增益运算放大器组成的运放芯片D258,可应用于音频信号处理系统上
[云原生] Prometheus自动服务发现部署
IDEA Gradle Lombok错误:找不到符号 setter getter方法没有
LeetCode笔记:Weekly Contest 299
免费领取!TikTok Shop “全托管”黑五大促官方备战指南来啦!
http协议连接方式 —— 短连接和长连接(请求头Connection属性)
16、探究 Java 动态绑定机制和 this 的本质
WPF自定义快捷命令
- 原文地址:https://blog.csdn.net/m0_45085885/article/details/125509729