力扣94二叉树的中序遍历

力扣94二叉树的中序遍历

题目描述

给定一个二叉树的根节点 root ，返回 它的 中序 遍历 。进阶: 递归算法很简单，你可以通过迭代算法完成吗？

输入输出详情

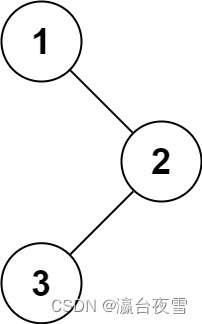
输入：root = [1,null,2,3]
输出：[1,3,2]
1
2

输入：root = []
输出：[]
1
2

输入：root = [1]
输出：[1]
1
2

算法1，使用递归完成中序，前序，后序遍历

//采用递归的思想，中序遍历
        vector<int>inorderTraversal(TreeNode*root)
        {
            if(root==nullptr)
            {
                return res;
            }
            inorderTraversal(root->left);
            res.push_back(root->val);
            inorderTraversal(root->right);
            return res;
        }
        //前序遍历，先将根结点存储再存储左节点，然后右节点
        vector<int>preOrderTraversal(TreeNode*root)
        {
            if(root==nullptr)
            {
                return res;
            }
            res.push_back(root->val);
            preOrderTraversal(root->left);
            preOrderTraversal(root->right);
            return res;
        }
        //后序遍历，先左再右最后再根
        vector<int>postOrderTraversal(TreeNode*root)
        {
            if(root==nullptr)
            {
                return res;
            }
            postOrderTraversal(root->left);
            postOrderTraversal(root->right);
            res.push_back(root->val);
            return res;
        }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

算法2，使用栈进行迭代计算

//使用迭代和栈进行实现
        vector<int>inorderTraversal2(TreeNode*root)
        {
            vector<int>res;
            //建立堆栈保存当前的结点
            stack<TreeNode*>stk;
            //当结点存在的时候，并且堆栈不为空
            while(root!=nullptr||!stk.empty())
            {
                while(root!=nullptr)
                {
                    stk.push(root);
                    //当结点不为空的时候则结点向左结点移动
                    root=root->left;
                }
                //当root当前指的值为空的时候，那么就要将其向右移动，并将该值入队列
                root=stk.top();
                stk.pop();
                res.push_back(root->val);
                root=root->right;
            }
            return res;
        }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

算法3，使用莫里斯中序遍历

 //使用莫里斯方法进行实现
     vector<int>inorderTraversal3(TreeNode*root)
     {
        vector<int>res;
        TreeNode*preDecessor=nullptr;

        while(root!=nullptr)
        {
            if(root->left!=nullptr)
            {
                //preDecessor结点就是当前root结点往左走一点，然后一直向右走直至无法走到为止
                preDecessor=root->left;
                //当preDecessor的右节点存在并且不等于根结点时候，preDecessor一直向右移动
                while (preDecessor->right!=nullptr&&preDecessor->right!=root)
                {
                    preDecessor=preDecessor->right;
                }
                //如果preDecessor的右指针，继续遍历左子树
                if(preDecessor->right==nullptr)
                {
                    preDecessor->right=root;
                    root=root->left;
                }

                //此时左子树已经访问完了，断开连接
                else{
                    res.push_back(root->val);
                    preDecessor->right=nullptr;
                    root=root->right;
                }
                
            }
            else{
                res.push_back(root->val);
                root=root->right;
            }
        }
        return res;
     }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40