K M P模式匹配

#include <bits/stdc++.h>
using namespace std;
#define N 100
char s[N];
char m[N];
int nxt[N];
void process()
{
    nxt[1] = 0;
    int len = strlen(m+1);
    for(int i = 2, j = 0; i <= len; i++)//注意：必须要从2开始。
    {
        while(j > 0 && m[i] != m[j+1]) j = nxt[j];
        if(m[i]==m[j+1]) j++;
        nxt[i] = j;
    }
}
void KMP()
{
    int mlen = strlen(m+1);
    int slen = strlen(s+1);
    for(int i = 1, j = 0; i <= slen; i++)
    {
        while(j > 0 && (s[i] != m[j+1] || j == mlen)) j = nxt[j];
        if(s[i] == m[j+1]) j++;
        if(j==mlen) printf("%d ", i-j+1);
    }
}
int main()
{
    scanf("%s%s", s+1, m+1);
    process();
    KMP();
    
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

AcWing\141. 周期

思路：

1. 在KMP字符串匹配中，并不会直接考KMP，而是会考KMP的引理。

2. 也就是：定义nxt[i]是指当前位置下的最大数,这个最大的数字所具有的性质就是使得1_{nxt[i]和i-nxt[i]+1}len相等。

3. 对于任意一个候选项j，若存在一个小于j的候选项，那么这个候选项最大就是nxt[j]。

4. 对于这道题目，同样也有一个定理：

5. 存在循环元的充分必要条件就是：S[1~ j] == S[len-j+1~len]这个字符串是相等的，并且len-j可以整除len

6. 充分性：因为len-j可以整除，并且倍数，很容易联想到

7. 每次取前三个，然后以此类推。

8. 必要性显然得证。

错误答案

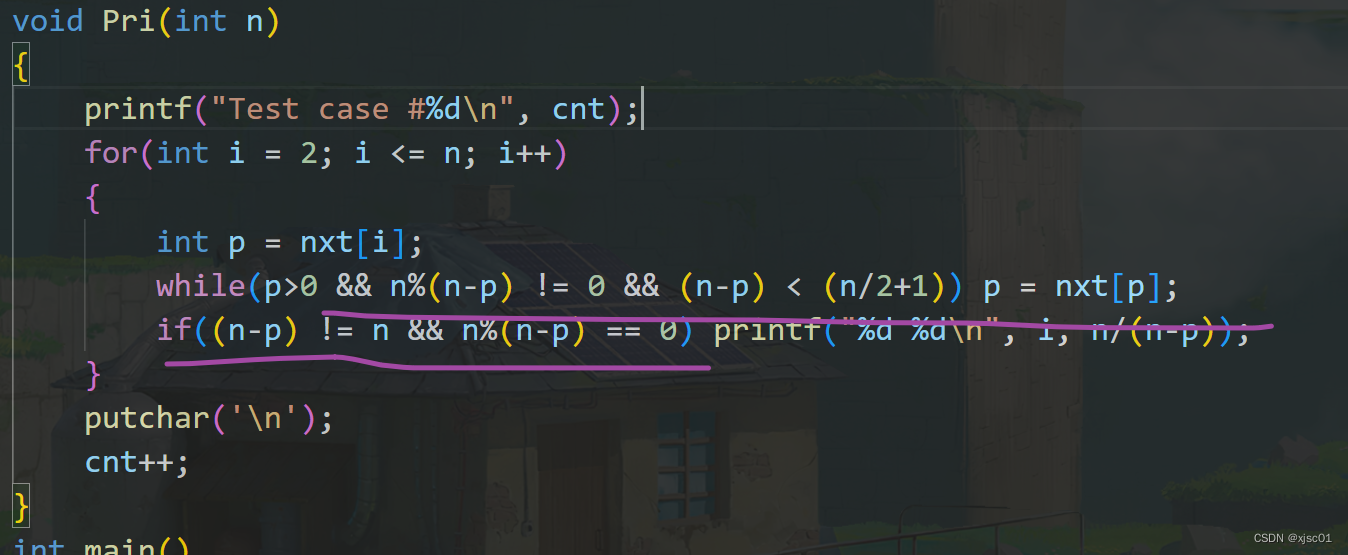
注意，我这里明显具有多余的内容。
假如我的i-nxt【i】不能整除i，
这个的意思就是这个子串是以i-nxt【i】为周期的，只不过是最后没有完整的周期。如果我在对nxt【i】求出了nxt，这样的周期一定是最一开始的倍数。既然最一开始的都没有办法整除，那么他的倍数就跟没办法整除

#include <bits/stdc++.h>
using namespace std;
#define N 1000010
char buf[N];
int nxt[N];
int cnt = 1;
void Pri(int n);
void cal(int len)
{
    scanf("%s", buf+1);
    nxt[1] = 0;
    for(int i = 2, j = 0; i <= len; i++)
    {
        while(j > 0 && buf[i] != buf[j+1]) j = nxt[j];
        if(buf[i] == buf[j+1]) j++;
        nxt[i] = j;
    }
    Pri(len);
    
}
void Pri(int n)
{
    printf("Test case #%d\n", cnt);
    for(int i = 2; i <= n; i++)
    {
        int p = nxt[i];
        if((i-p) != i && i%(i-p) == 0) printf("%d %d\n", i, i/(i-p));
    }
    putchar('\n');
    cnt++;
}
int main()
{
    int n;
    while(scanf("%d", &n) && n) cal(n);
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

最小表示法

背景：

对于一个循环字符串（心也可以清，也可以清心，。。。。）

把他们都视为是一样的，那么就应该有一种唯一的表示方法。

通过下面的方法，可以以$O(N)$的时间复杂度求出最小表示的字符串。

在这里，我们通过不断排除不可能的结果，最后存在的就是打遍天下无敌手。

代码&&解析

#include <bits/stdc++.h>
using namespace std;
#define N 200
char s[2*N];
char lest[N];
int porcess()
{
    int n = strlen(s+1);
    for(int i = 1; i <= n; i++) s[i+n] = s[i];//把两份拼接起来。
    int i = 1, j = 2, k = 0;
    while(i <= n && j <= n)//如果有一个不再范围内，就说明比较完成
    {
        for(k = 0; k < n && s[i+k] == s[j+k]; k++);
        if(k == n) break;//如果要是比较了n次都是对的，则相当于已经比较完成
        if(s[i+k] > s[j+k])//对于i+m来说（i <= m <= k）,总会有一个x = j+m，使得在i+k处不一致，并且i+m不是最优。
        //通过这样一搞，极大地排除了不可能的选项，从而只有线性的复杂度。
        {
            i = i+k+1;
            if(i==j) i++;//别忘了++
        }
        else
        {
            j = j+k+1;
            if(i==j) j++;
        }
    }
    int cnt = 0;//把答案拷贝过去
    for(int x = min(i, j); x < min(i, j) + n; x++)//最小的哪一个是i与j中的打遍天下的（没有在n的外面）
    {
        lest[++cnt] = s[x];
    }
    lest[++cnt] = '\0';
}
int main()
{
    scanf("%s", s+1);
    porcess();
    printf("%s", lest+1);
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40