【数据结构】树（六）—— 二叉平衡树（C语言版）

前言

在 《树（五）—— 二叉排序树》一文中，对二叉排序树进行性能分析时可知，当为二叉排序树为完全二叉树时，其查找性能最佳，与二分查找类似。故需要对二叉排序树进行优化为二叉平衡树。

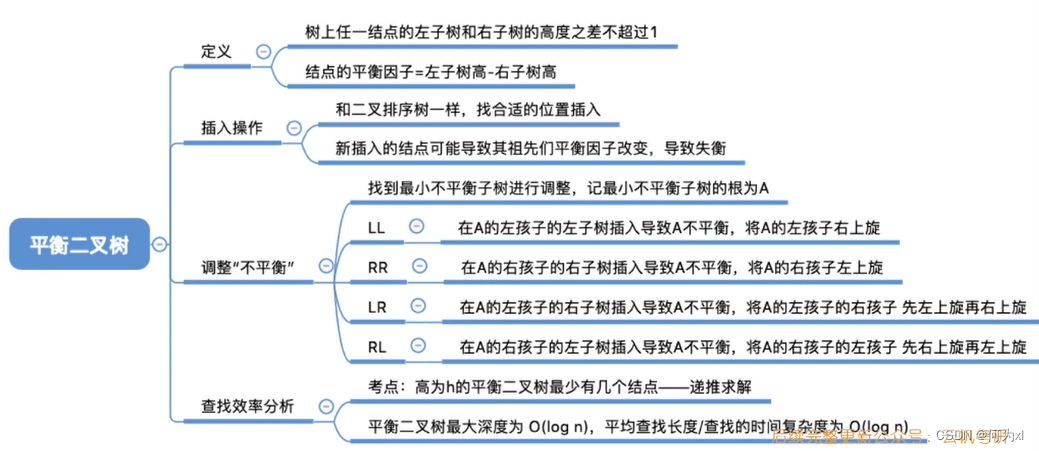
平衡二叉树的定义

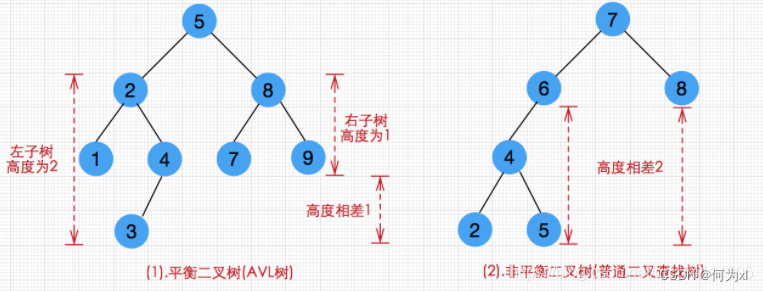
平衡二叉树可定义为或者是一棵空树，或者是具有下列性质的二叉树：其左子树和右子树均为平衡二叉树，且左子树和右子树的高度差的绝对值不超过1。

平衡二叉树(Balanced Binary Tree)又叫平衡二叉搜索树（Self-balancing Binary Search Tree），又被称为AVL树。

平衡因子：定义结点左子树与右子树的高度差为该结点的,则平衡二叉树结点的平衡因子的值只可能是-1、0或1。

注意：平衡二叉树一定是二叉排序树。含有n个结点的平衡二叉树的最大深度为O(log2(n))，即平衡二叉树的平均查找长度为O(log2(n))。

如下图所示为一棵平衡二叉树和一棵非平衡二叉树：

typedef struct AVLNode{
    int key;        //数据域
    int balance;    //平衡因子
    struct AVLNode *lchild,*rchild;
}AVLNode, *AVLTree;
1
2
3
4
5

平衡二叉树的插入

在二叉排序树中插入新结点后，如何保持平衡？

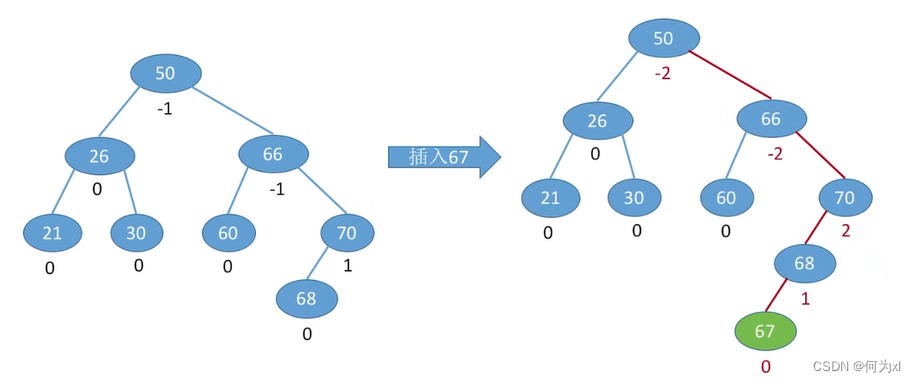
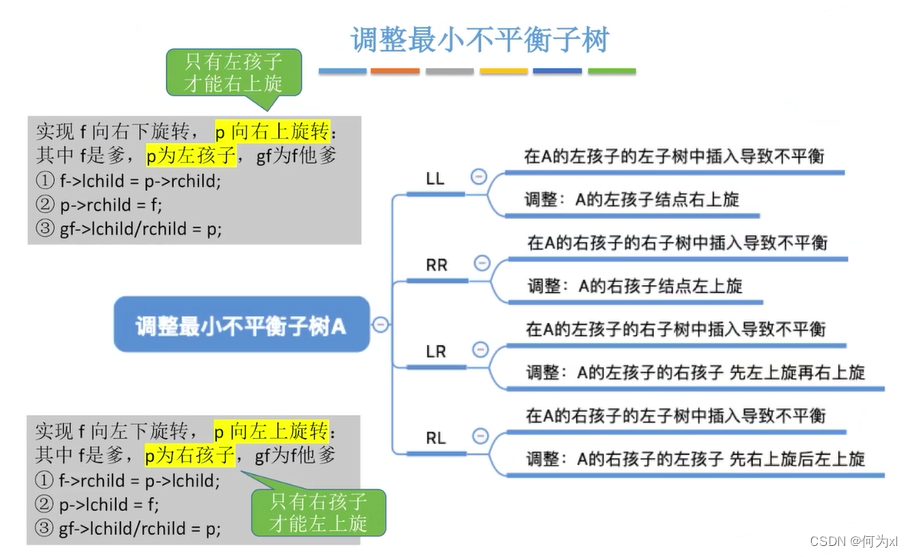
将最小不平衡子树调整平衡即可。

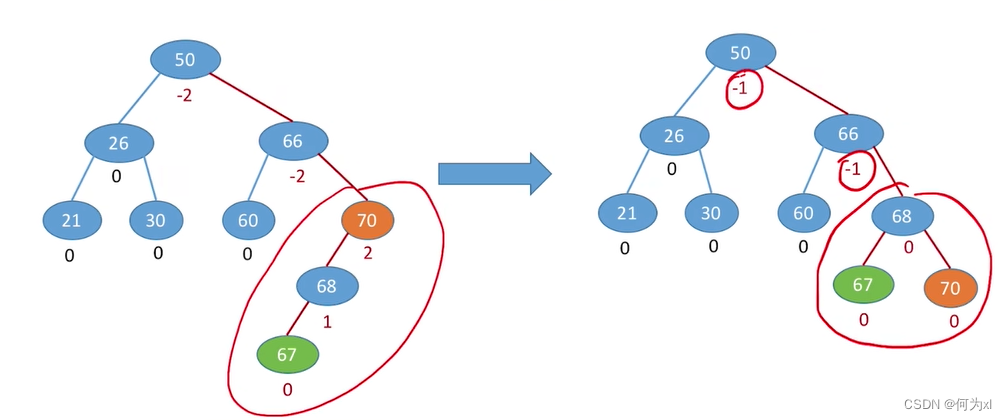
在插入操作中，只要将最小不平衡子树调整平衡，则其他祖先结点都会恢复平衡。

如何调整不平衡子树

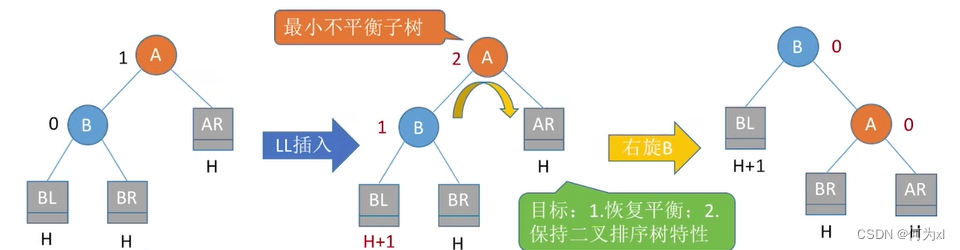
LL平衡旋转（右单旋转)。由于在结点A的左孩子(L)的左子树(L)上插入了新结点，A的平衡因子由1增至2，导致以A为根的子树失去平衡，需要一次向右的旋转操作。将A的左孩子B向右上旋转代替A成为根结点，将A结点向右下旋转成为B的右子树的根结点，而B的原右子树则作为A结点的左子树。

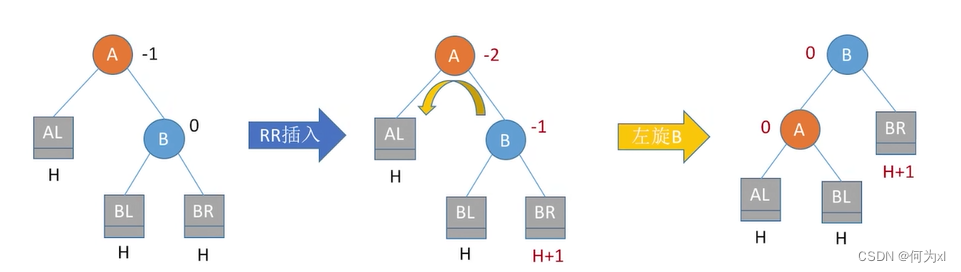
RR平衡旋转（左单旋转)。由于在结点A的右孩子(R）的右子树®上插入了新结点,A的平衡因子由-1减至-2，导致以A为根的子树失去平衡，需要一次向左的旋转操作。将A的右孩子B向左上旋转代替A成为根结点，将A结点向左下旋转成为B的左子树的根结点，而B的原左子树则作为A结点的右子树。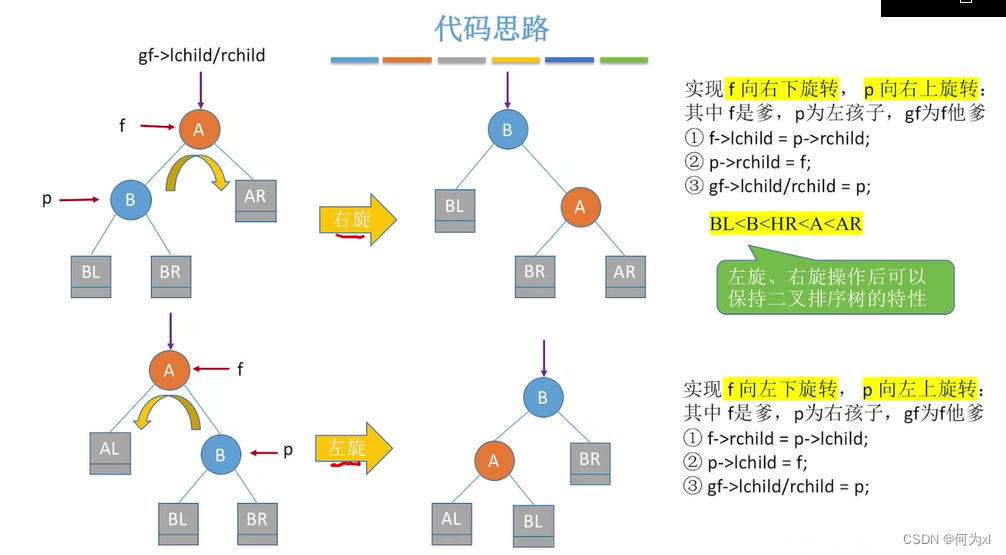

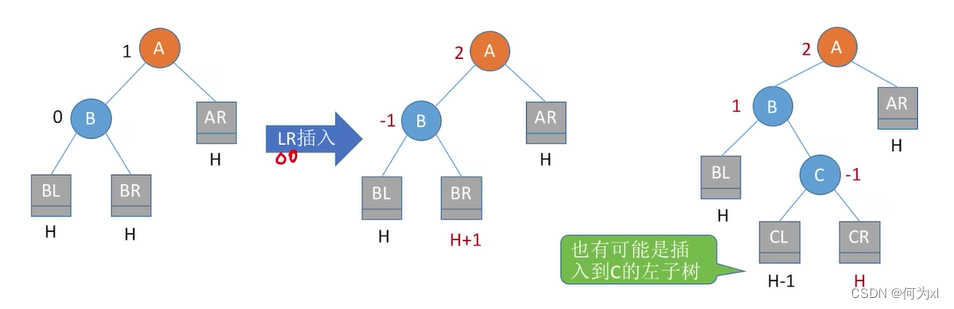
LR平衡旋转（先左后右双旋转)。由于在A的左孩子(L)的右子树(R）上插入新结点，A的平衡因子由1增至2，导致以A为根的子树失去平衡，需要进行两次旋转操作，先左旋转后右旋转。先将A结点的左孩子B的右子树的根结点C向左上旋转提升到B结点的位置，然后把该C结点向右上旋转提升到A结点的位置。

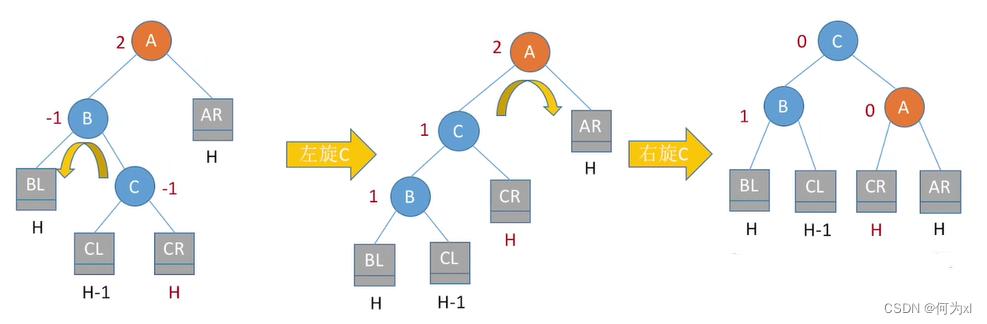
注意:LR和RL旋转时，新结点究竟是插入C的左子树还是插入C的右子树不影响旋转过程，而图5.30和图5.31中以插入C的左子树中为例。

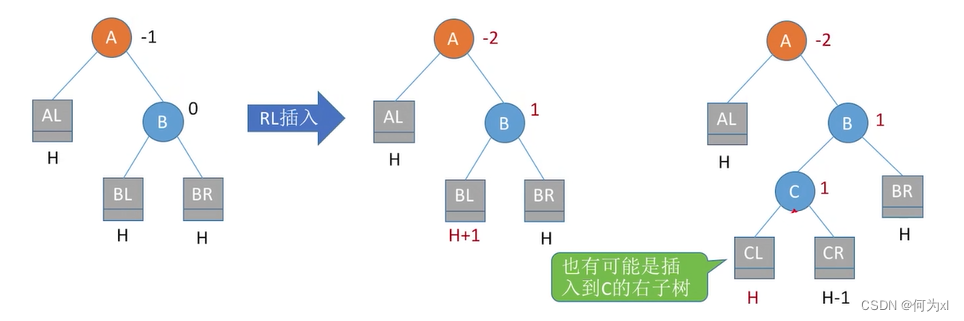
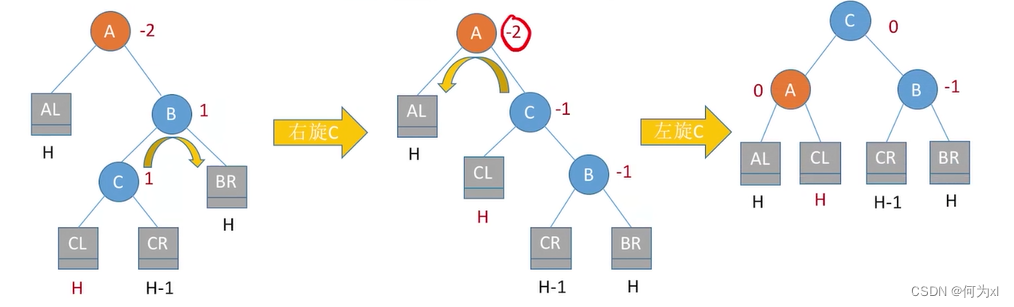
RL平衡旋转（先右后左双旋转)。由于在A的右孩子®的左子树(L)上插入新结点,A的平衡因子由-1减至-2，导致以A为根的子树失去平衡，需要进行两次旋转操作，先右旋转后左旋转。先将A结点的右孩子B的左子树的根结点C向右上旋转提升到B结点的位置，然后把该C结点向左上旋转提升到A结点的位置，

只有左孩子才能右上璇，只有右孩子才能左上璇

插入操作导致“最小不平衡子树”高度+1，经过调整后高度恢复。。

同理其他祖先结点也都会恢复

练习

查找效率分析

完整代码

package Tree;

public class AVLTree {
	public static void main(String[] args) {
		int[] arr= {10,11,7,6,8,9};
		AVL avlTree=new AVL();
		for(int i=0;i<arr.length;i++) {
			 avlTree.add(new Node(arr[i]));
		}
		
		System.out.println("初始平衡二叉树的中序遍历");
		avlTree.inOrder();
		System.out.println("双旋转处理后：");
		avlTree.inOrder();
	    System.out.println("树的高度=" + avlTree.getRoot().height()); // 3
	    System.out.println("树的左子树高度=" + avlTree.getRoot().leftHeight()); // 2
	    System.out.println("树的右子树高度=" + avlTree.getRoot().rightHeight()); // 2
	    System.out.println("当前的根结点=" + avlTree.getRoot());// 8
	    System.out.println("根节点的左结点=" + avlTree.getRoot().left);// 7
	    System.out.println("根节点的右结点=" + avlTree.getRoot().right);// 10
	}
}

class AVL{
	private Node root;
	
	public Node getRoot() {//获取根结点
		return root;
	}
	
	public void add(Node node) {//添加子结点
		if (root == null) {//若根结点为空直接让添加结点成为子结点
			root = node;
		} else {
			root.add(node);
		}
	}
	
	public void inOrder() {//中序遍历
		if(root!=null) {//若根结点不为空则调用结点的inOrder
			root.inOrder();
		}else {
			System.out.println("平衡二叉树为空，无法遍历！");
		}
	}
}

class Node{
	int value;
	Node left;
	Node right;
	
	 public Node(int value) {//Node的构造函数
		 this.value=value;
	 }
	 
	@Override
	public String toString() {//重写toString方法
		return "Node [value=" + value + "]";
	}
	 
	public int height() {//返回以该结点为根结点的树的高度
		return Math.max(left==null ? 0:left.height(), right==null ? 0:right.height())+1;
	}
	
	public int leftHeight() {//返回左子树的高度
		if(left==null) {//左子树为空直接返回0
			return 0;
		}
		return left.height();//递归左子树的高度
	}
	
	public int rightHeight() {//返回右子树的高度
		if(right==null) {//右子树为空直接返回0
			return 0;
		}
		return right.height();//递归右子树的高度
	}
	
	//RR平衡旋转（左单旋转）
	private void leftRotate() {
		Node newNode =new Node(value);//创建一个新的结点newNode
		newNode.left=left;//将新结点的左子树设置为当前结点的左子树
		newNode.right=right.left;//将新结点的右子树设置为当前结点的右子树的左子树
		value=right.value;//将当前结点的值换为右子结点的值
		right=right.right;//将当前结点的右子树设置成右子树的右子树
		left=newNode;//将当前结点的左子树设置成新结点
	}
	
	//LL平衡旋转（右单旋转）
	private void rightRotate() {
		Node newNode =new Node(value);//创建一个新的结点newNode
		newNode.right=right;//将新结点的右子树设置为当前结点的右子树
		newNode.left=left.right;//将新结点的左子树设置为当前结点的左子树的右子树
		value=left.value;//将当前结点的值换为左子结点的值
		left=left.left;//将当前结点的左子树设置成左子树的左子树
		right=newNode;//将当前结点的右子树设置成新结点
	}
	
	public void add(Node node) {//添加子结点
		if (node == null) {//添加结点为空
			return;
		}
		if (node.value < this.value) {//添加结点值小于当前结点值,根据二叉排序树定义应向左边寻找
			if (this.left == null) {//当前结点没有左孩子直接放在当前结点左边
				this.left = node;
			} else {
				this.left.add(node);//否则递归向当前结点的左子树遍历
			}
		} else {//添加结点值大于等于当前结点值,根据二叉排序树定义应向右边寻找
			if (this.right == null) {//当前结点没有右孩子直接放在当前结点右边
				this.right = node;
			} else {
				this.right.add(node);//否则递归向当前结点的右子树遍历
			}
		}
		
		if(rightHeight()-leftHeight()>1) {//当添加完一个结点后,如果: (右子树的高度-左子树的高度) > 1 ,左旋转
			if(right!=null&&right.leftHeight()>right.rightHeight()) {//若它的右子树的左子树的高度大于它的右子树的右子树的高度
				right.rightRotate();//RL平衡旋转（先右后左双旋转）
				leftRotate();
			}else {
				leftRotate();//RR平衡旋转（左单旋转）
			}
			return;
		}
		
		if(leftHeight()-rightHeight()>1) {//当添加完一个结点后,如果 :(左子树的高度 - 右子树的高度) > 1, 右旋转
			if(left!=null&&left.rightHeight()>left.leftHeight()) {//若它的左子树的右子树高度大于它的左子树的左子树的高度
				left.leftRotate();//LR平衡旋转（先左后右双旋转）
				rightRotate();
			}else {
				rightRotate();//LL平衡旋转（右单旋转）
			}
		}
	}
	
	public void inOrder() {//中序遍历
		if(this.left!=null) {
			this.left.inOrder();
		}
		System.out.println(this);
		if(this.right!=null) {
			this.right.inOrder();
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147

中序遍历获得一个递增数列，所以删除非叶子结点替换的结点一个为中序遍历后的第一个结点
二叉排序树： 左<中<右（可能有多个）

大根堆：跟结点大于左右子树的结点值