-
数据结构与算法:树 二叉树入门(一)
Tips: 采用java语言,关注博主,底部附有完整代码
工具:IDEA
本系列介绍的是数据结构: 树
这是第一篇目前计划一共有12篇:
- 二叉树入门 (本篇)
- 顺序二叉树
- 线索化二叉树
- 堆排序
- 赫夫曼树(一)
- 赫夫曼树(二)
- 赫夫曼树(三)
- 二叉排序树
- 平衡二叉树
- 2-3树,2-3-4树,B树 B+树 B*树 了解
- 红黑树(一)
- 红黑树(二)
敬请期待吧~~
高光事例:
遍历 image 前序遍历 
中序遍历 
后续遍历 
层序遍历 
常用术语
首先先来看一颗简单的树
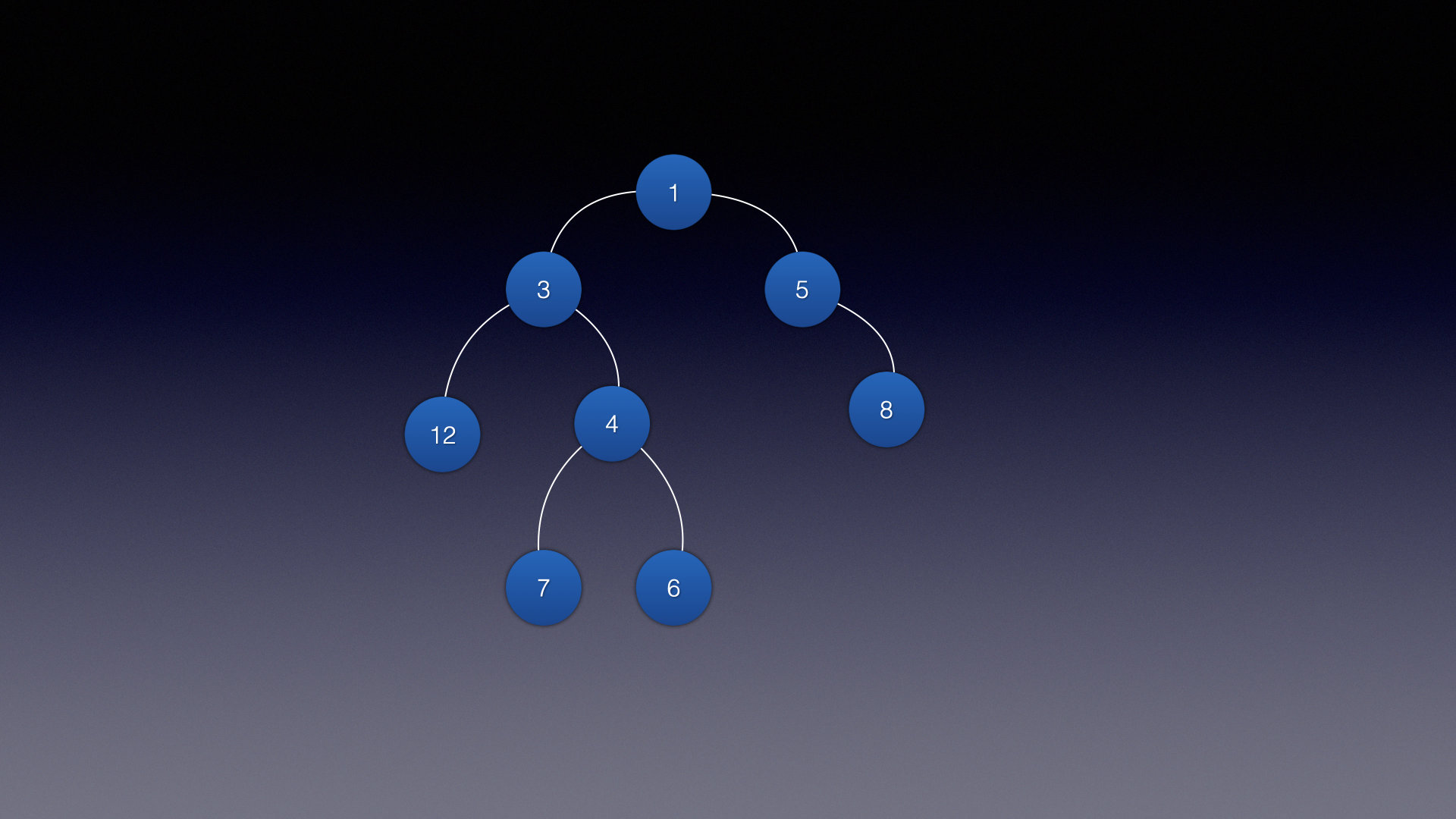
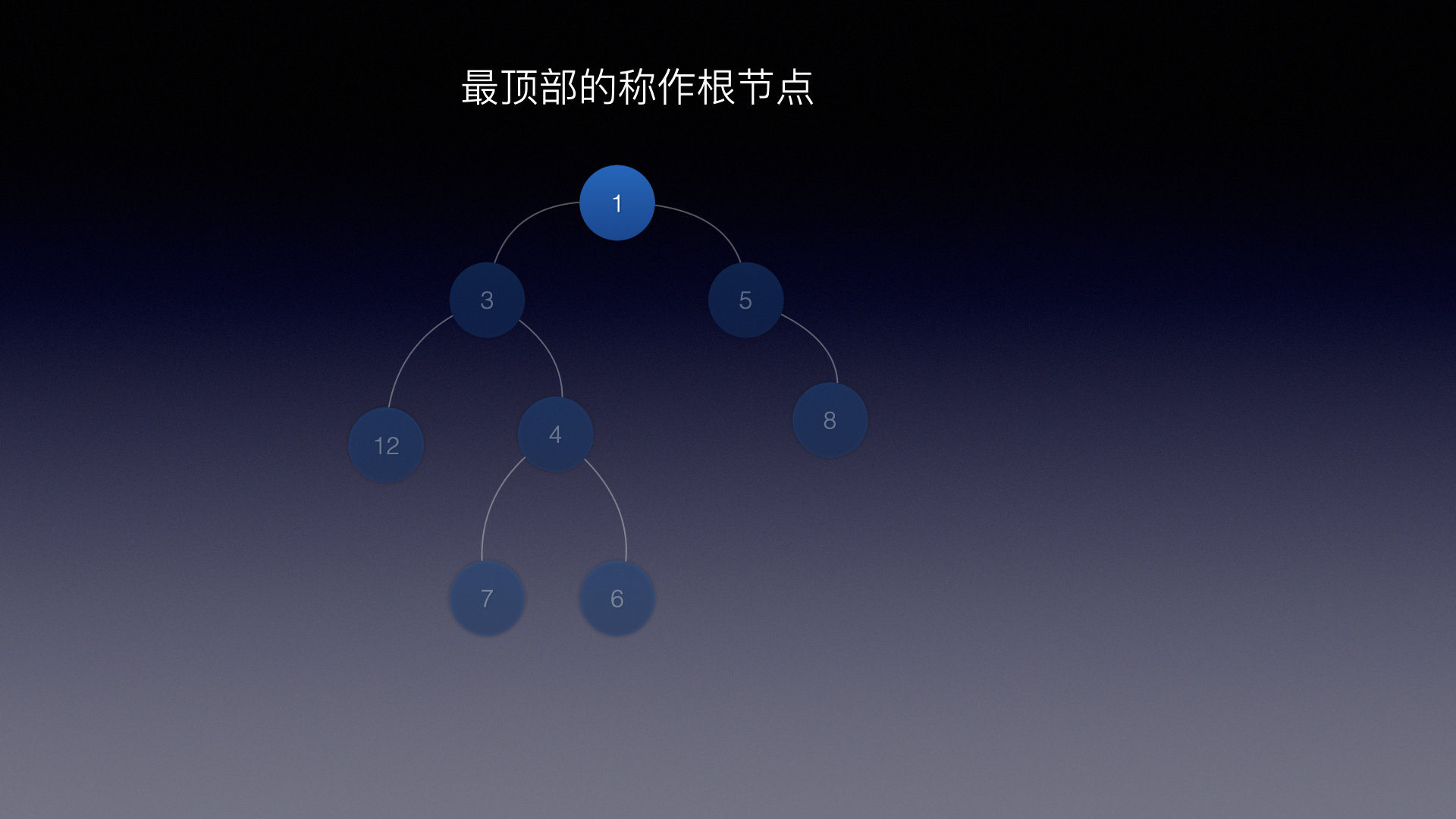
首先最顶部叫做树根,也叫根节点
树根左右两侧分别有两个结点
- 左子结点
- 右子结点
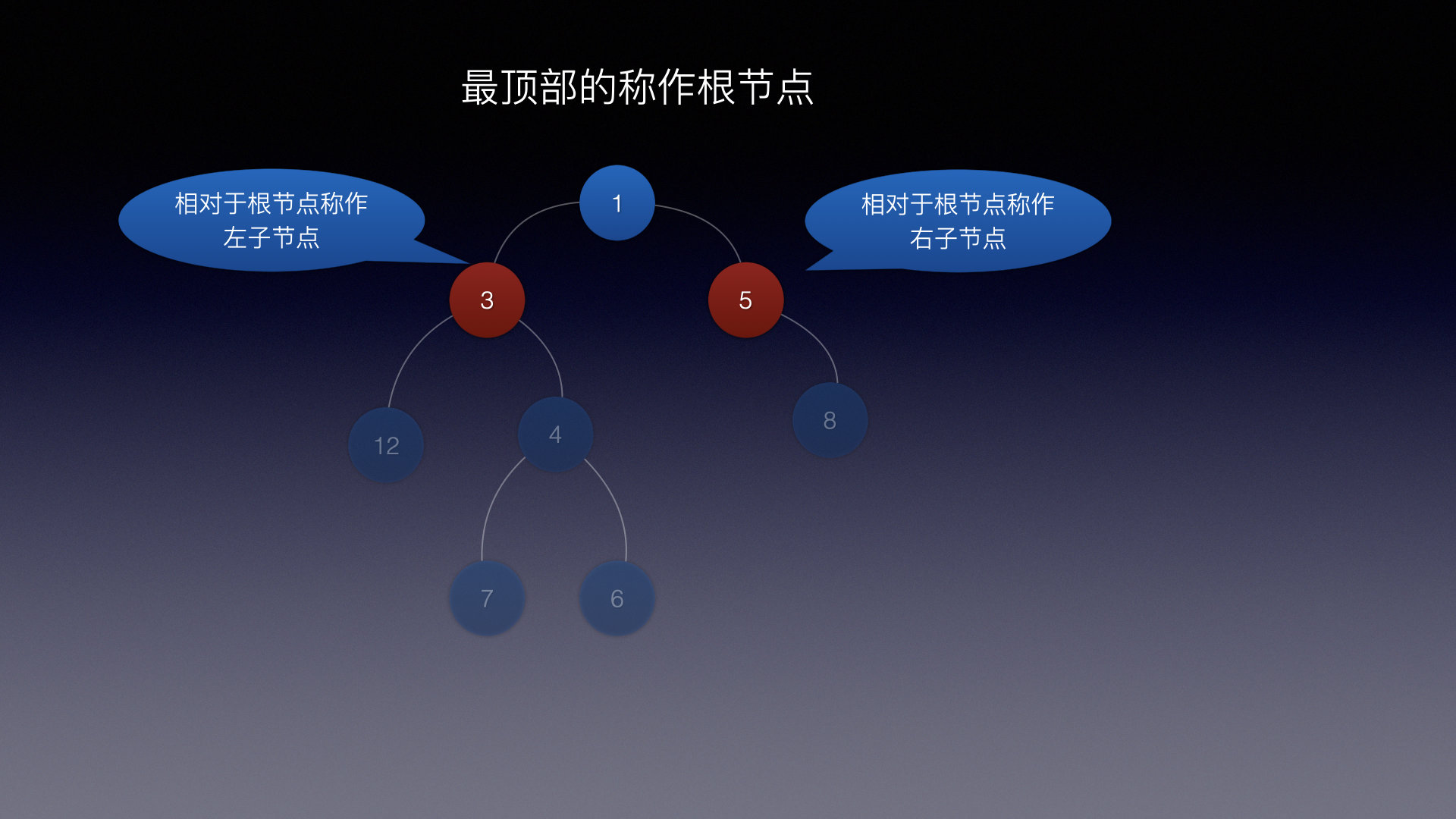
左子结点和右子结点统称为子结点
那么换句话说就是 1的子结点有3 和 5
或者
- 1的左子结点是 3
- 1的右子结点是 5
此时3 是1的左子结点 ,3也是 12的父结点
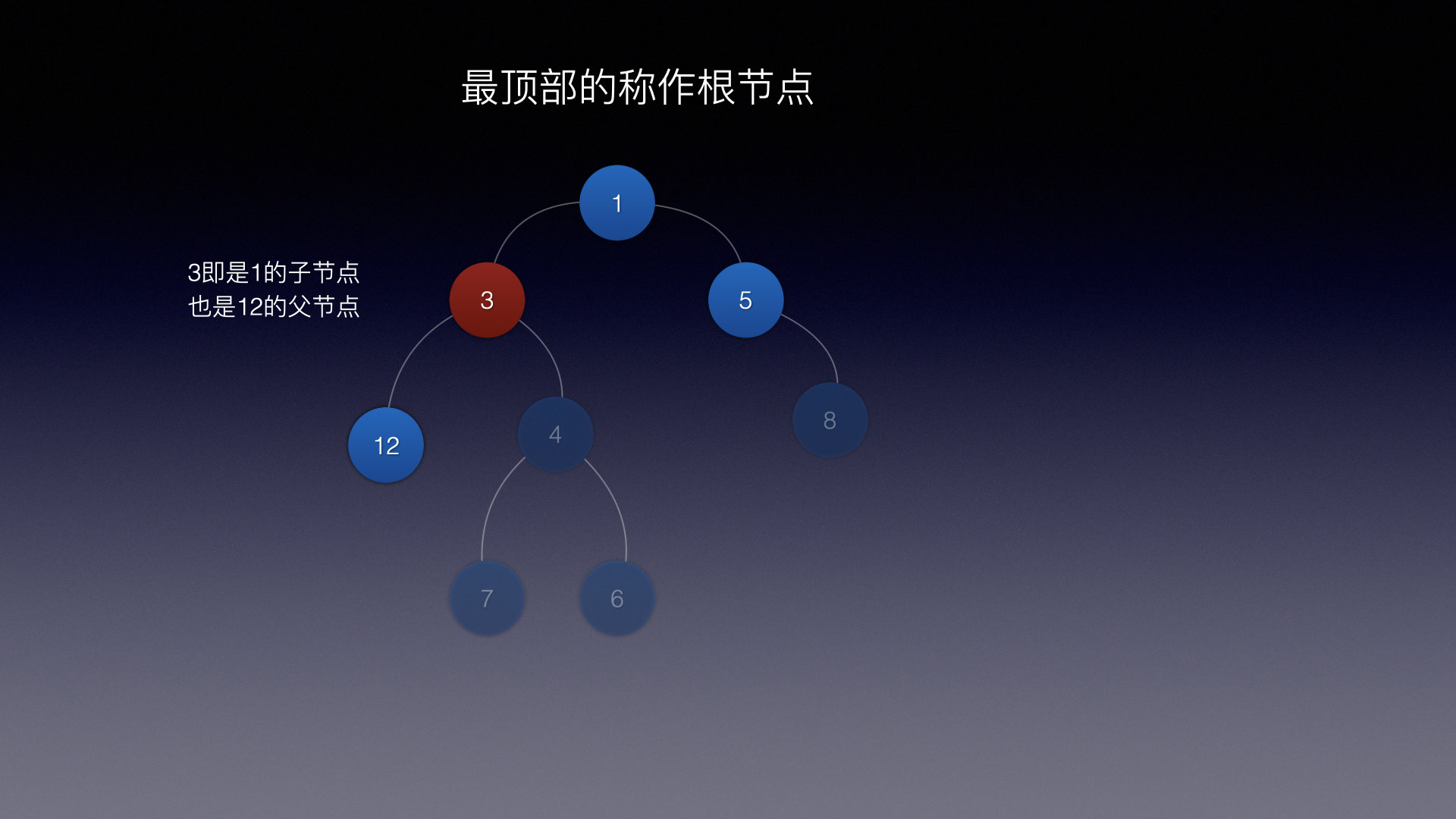
通俗的说:3又是父亲又是儿子
- 3是12的父亲
- 3是1的儿子
其他叫法相同
例如
-
7的父结点是4
-
8的父结点是5
-
4的右子结点是6
正常情况下一颗树都有2个结点(左子结点 / 右子结点),如果一颗树只有一边有结点,例如这样:
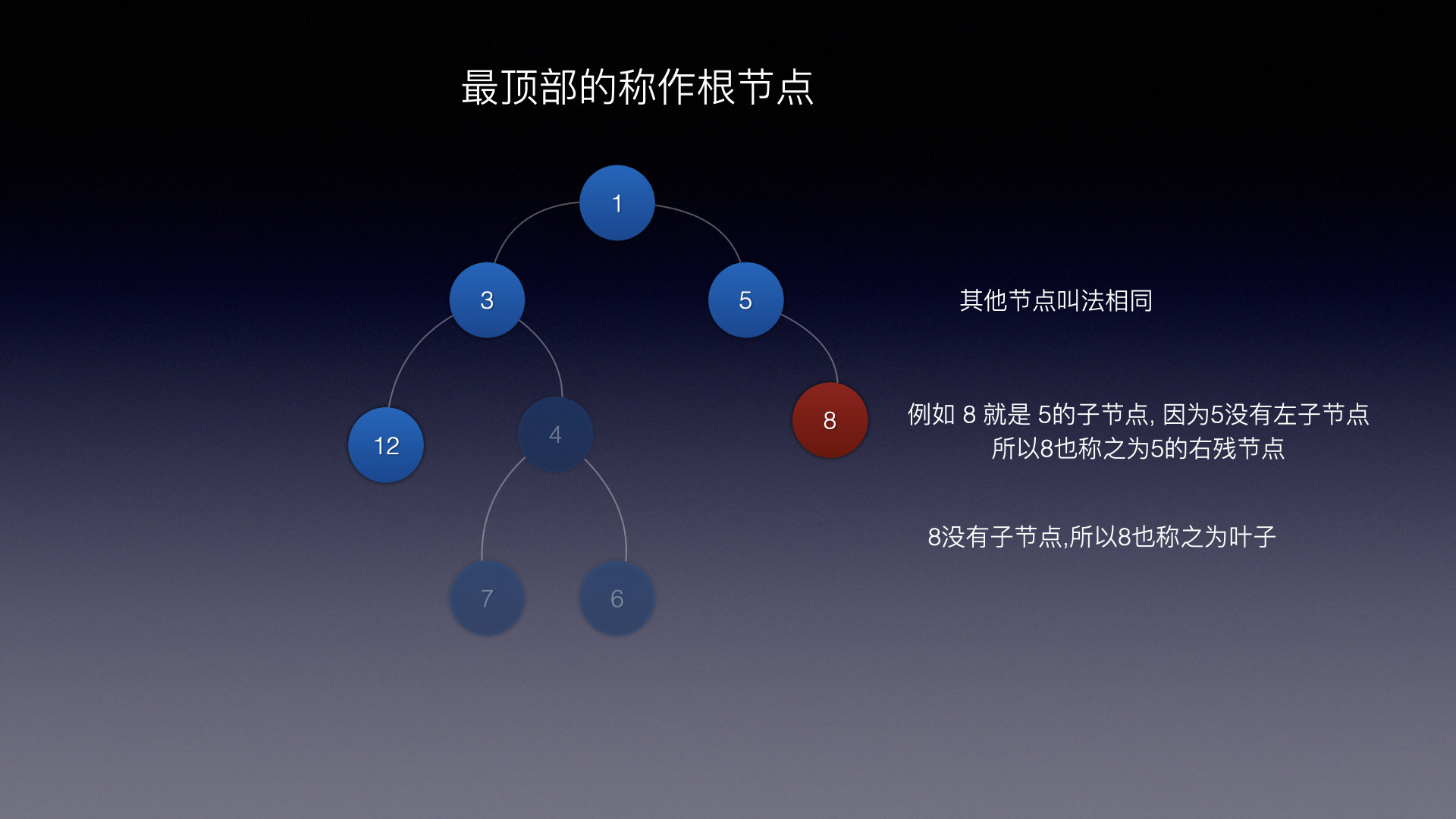
那么8也可以叫做5的右残结点
此时8没有子结点,也可以叫叶子 或 叶子结点
在这颗树中12, 7, 6, 8 都是叶子结点
只要有父结点和子结点,那么这个整体就是一颗子树,例如这些
子树1 子树2 子树3 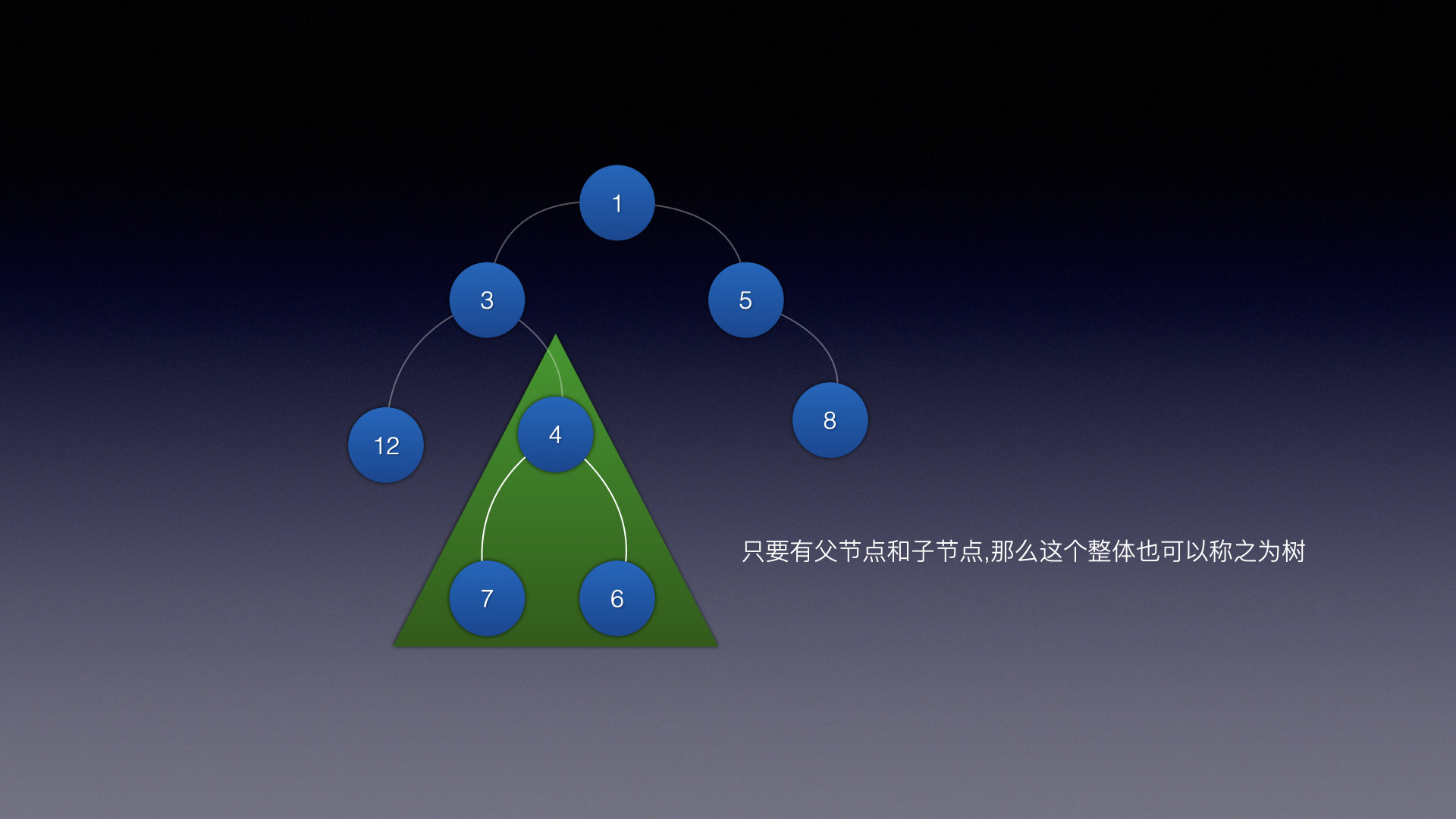

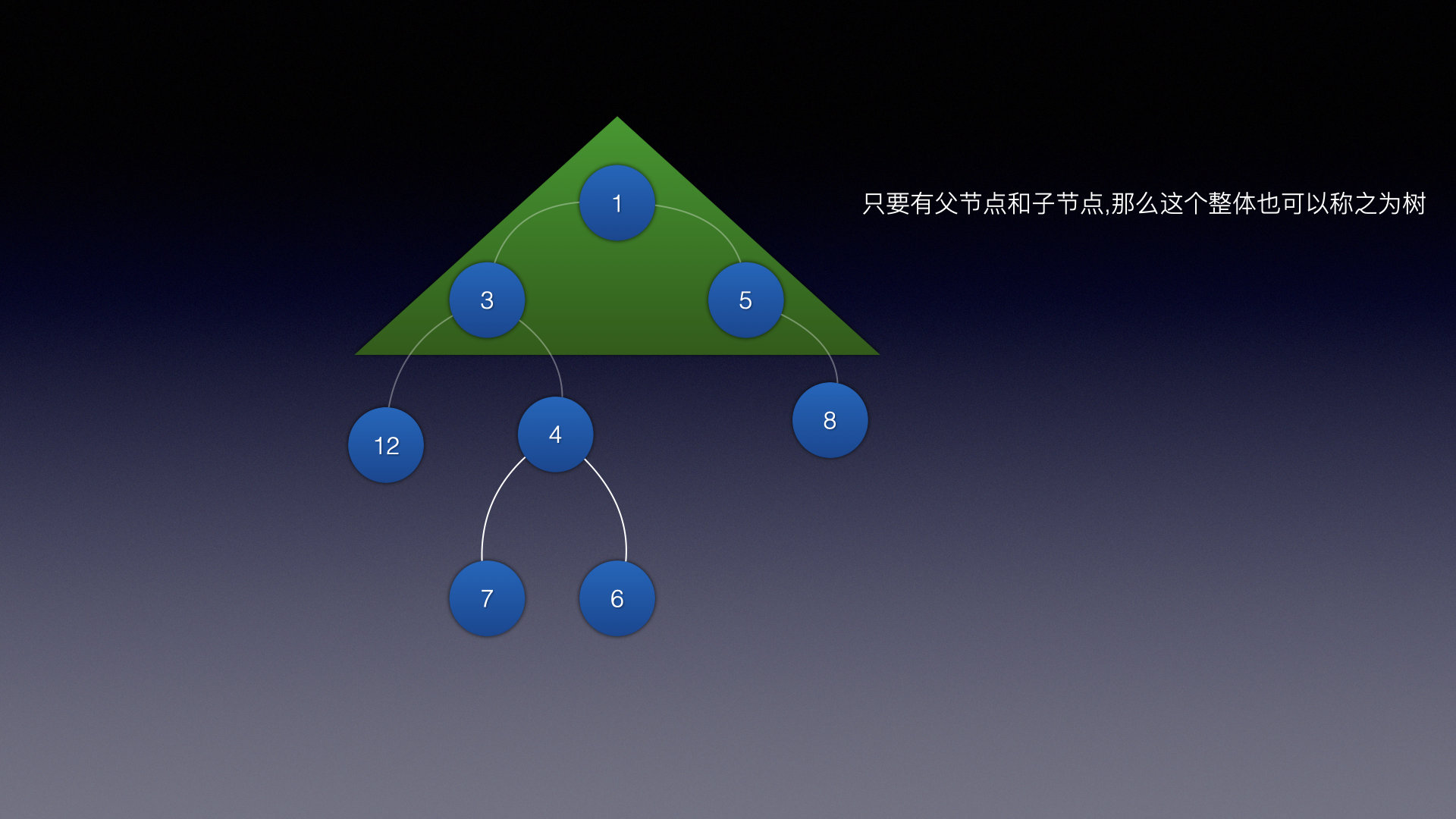
树也可以分层,例如这样:
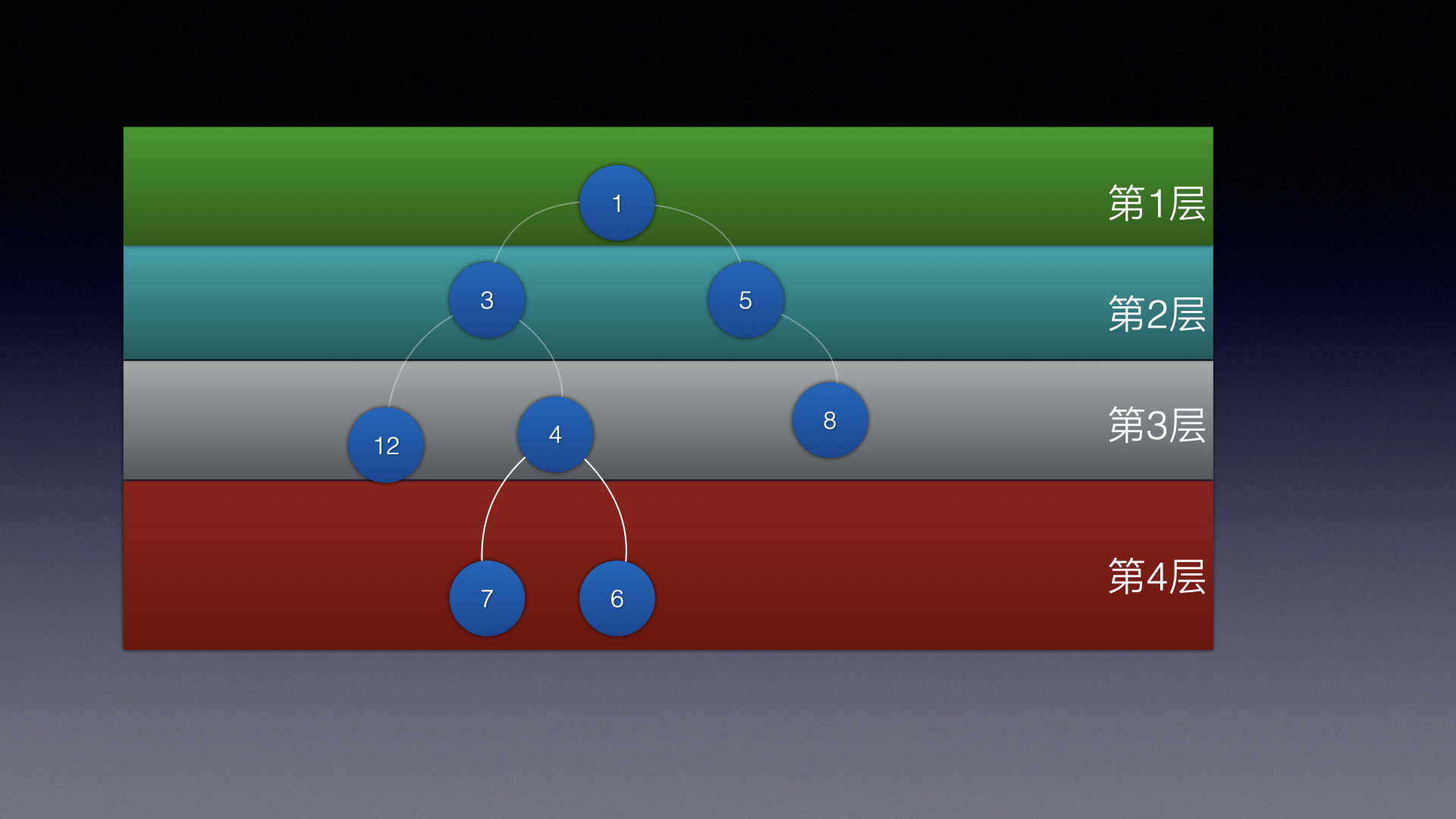
节点的层次:从根节点开始,假设根节点为第1层,根节点的子节点为第2层,依此类推,如果某一个节点位于第L层,则其子节点位于第L+1层 。
其他叫法可以参考:百度百科
树的形态
树的形态大致有3种:
- 完美二叉树
- 完全二叉树
- 完满二叉树 (满二叉树)
name image 描述 完美二叉树 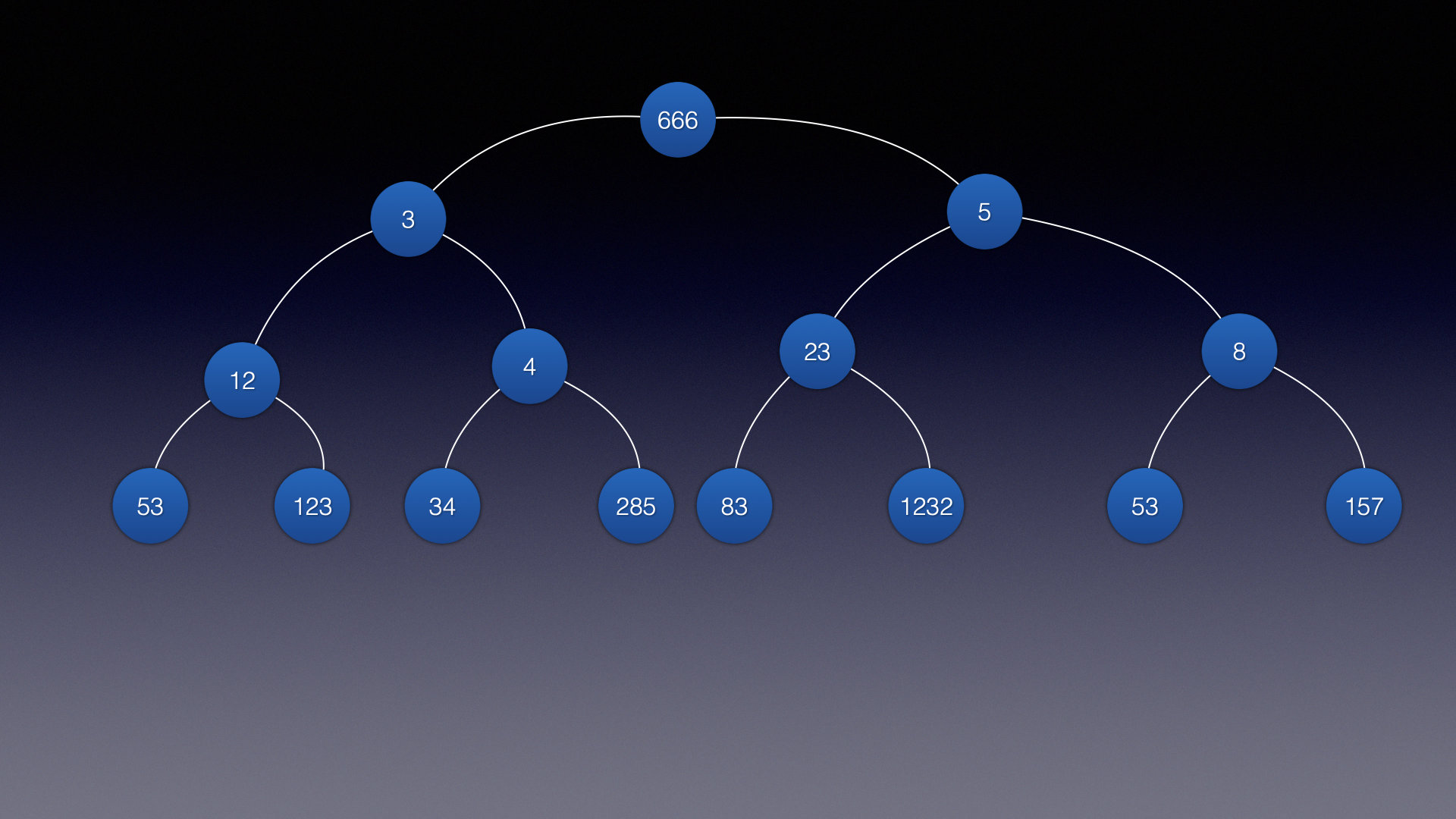
除了叶子结点之外的每一个结点都有2个孩子,并且每一层都被完全填充 完全二叉树 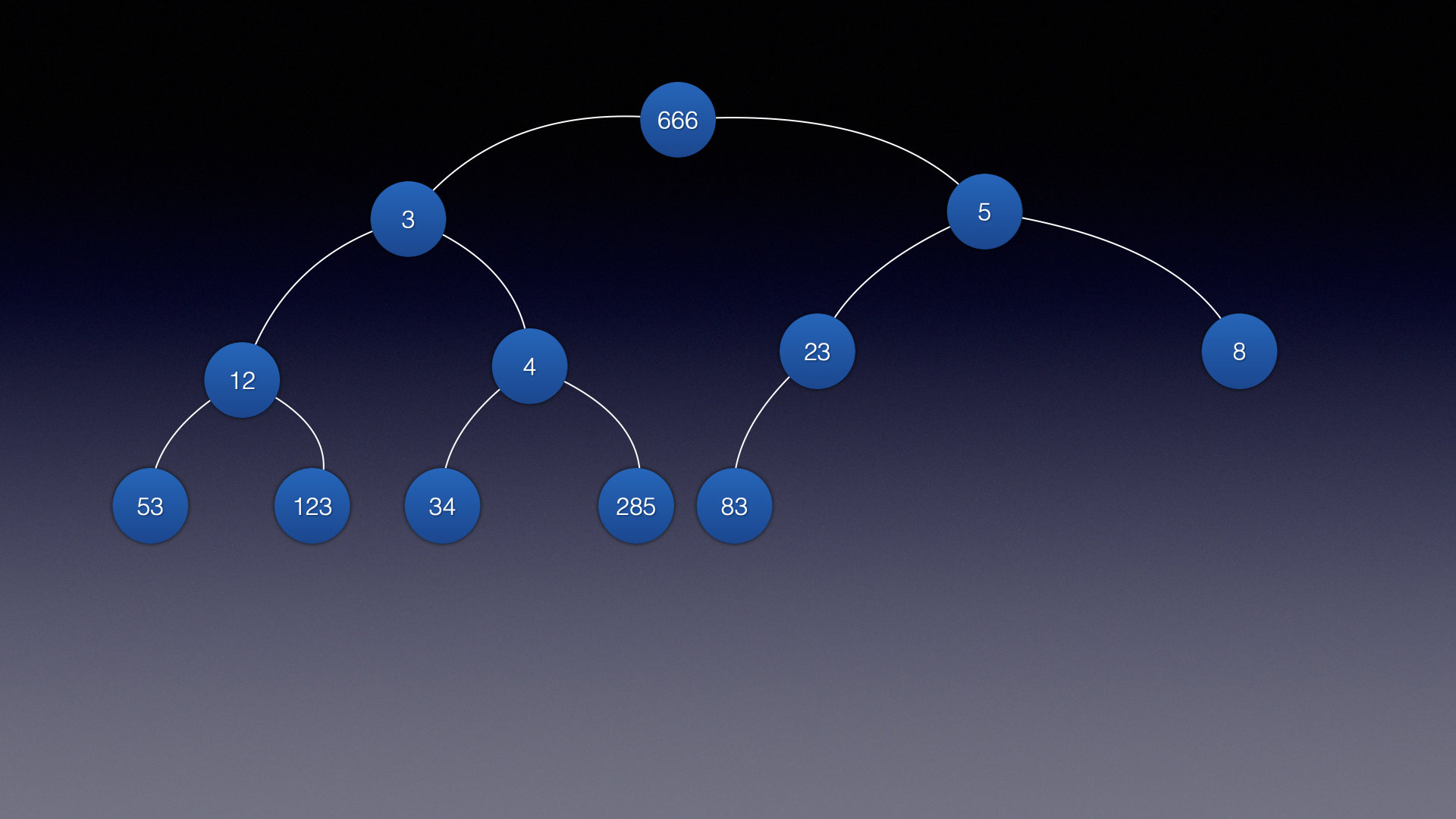
最后一层的结点全部靠左,除了最后一层外其他层都完全填充 完满二叉树 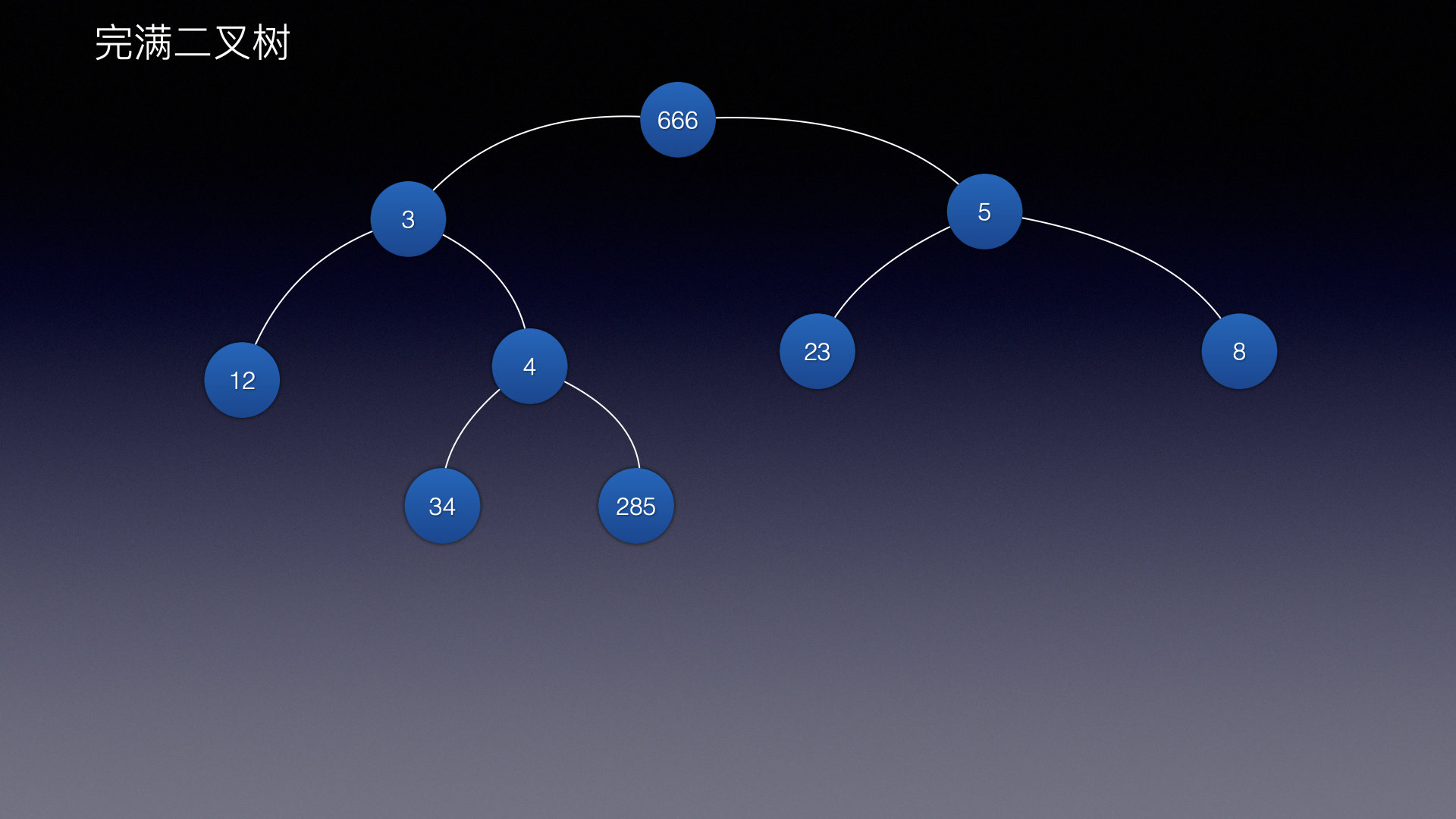
除了叶子结点外,如果你有孩子,那么必须有2个孩子 三者的区别:
- 完美二叉树一定是完全二叉树,完满二叉树
- 完全二叉树不一定是完满二叉树
- 如果一颗树是完满二叉树和完全二叉树,那么也不一定是完美二叉树
- 完满二叉树不一定是完全二叉树
这些话有点绕,只要把这三种树的特点记住,自己想一想就清晰啦~
创建一颗树
先创建一个结点类
public static class TreeHeroNode { public int id; public String name; // 左节点 public TreeHeroNode leftNode; // 右节点 public TreeHeroNode rightNode; public TreeHeroNode(int id, String name) { this.id = id; this.name = name; } @Override public String toString() { return "TreeHeroNode{" + "id=" + id + ", name='" + name + '\'' + '}'; } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
在创建一个树类
public class BinaryTree { private final TreeHeroNode root; /** * @param root 跟节点 */ public BinaryTree(TreeHeroNode root) { this.root = root; if (this.root == null) { throw new NullPointerException("空树?"); } } public static class TreeHeroNode {....} }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
直接传入根节点就可以啦
使用:
BinaryTree.TreeHeroNode root = new BinaryTree.TreeHeroNode(1, "张飞"); BinaryTree.TreeHeroNode node3 = new BinaryTree.TreeHeroNode(3, "关羽"); BinaryTree.TreeHeroNode node5 = new BinaryTree.TreeHeroNode(5, "吕布"); BinaryTree.TreeHeroNode node12 = new BinaryTree.TreeHeroNode(12, "马超"); BinaryTree.TreeHeroNode node4 = new BinaryTree.TreeHeroNode(4, "邢道荣"); BinaryTree.TreeHeroNode node8 = new BinaryTree.TreeHeroNode(8, "刘备"); BinaryTree.TreeHeroNode node7 = new BinaryTree.TreeHeroNode(7, "曹操"); BinaryTree.TreeHeroNode node6 = new BinaryTree.TreeHeroNode(6, "诸葛亮"); // 设置节点 root.leftNode = node3; root.rightNode = node5; node3.leftNode = node12; node3.rightNode = node4; node4.leftNode = node7; node4.rightNode = node6; node5.rightNode = node8; BinaryTree binaryTree = new BinaryTree(root);- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
此时结构图长这样:
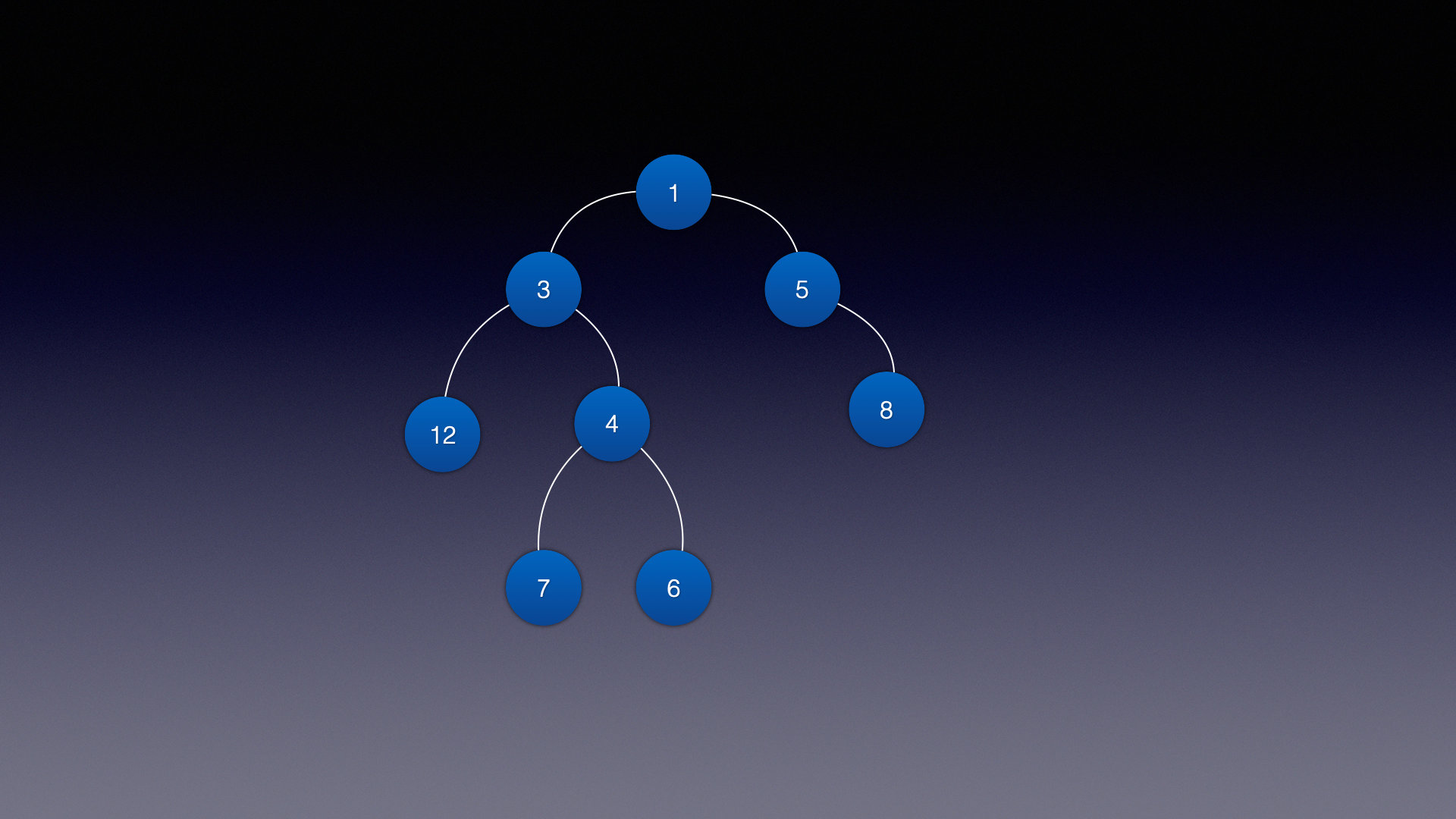
可能有初学者朋友看到这里有点问题,为什么这里不直接写一个add() 方法添加呢…
因为: 树和其他结构不同,如果细分的话有
- 有序树
- 无序树
当前就是无序树,因为他没有顺序,所以说一个新结点加在左侧或者右侧根本控制不了,等后面讲到有序树的时候,自然就有添加方法啦!
本篇只需要把创建一颗树和树的遍历,查找,删除搞会即可!
树的遍历
树的遍历分为4种情况
-
前序遍历
-
中序遍历
-
后序遍历
-
层序遍历
前序遍历
前序遍历规则:
先遍历父结点,然后左子结点,最后右子结点,如果有子结点那么先遍历子结点
先来看一眼效果图:

来看一眼代码:
public static class TreeHeroNode { // 左节点 public TreeHeroNode leftNode; // 右节点 public TreeHeroNode rightNode; // 前序遍历 public void show() { // 先打印父结点 System.out.println(this); // 在打印左子结点 if (leftNode != null) { leftNode.show(); } // 在打印右子结点 if (rightNode != null) { rightNode.show(); } } @Override public String toString() { return "TreeHeroNode{" + "id=" + id + ", name='" + name + '\'' + '}'; } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
这里采用的是递归的办法进行遍历,如果递归看不懂,可以使用debug多走几次!
重点是思路!
中序遍历
能看懂前序遍历中序遍历就简单多了:
中序遍历规则:
先遍历左子结点,在遍历父结点,最后遍历右子结点,有子结点先遍历子结点
效果图:

代码:
public static class TreeHeroNode { // 左节点 public TreeHeroNode leftNode; // 右节点 public TreeHeroNode rightNode; // 中序遍历 public void show() { // 先打印左子结点 if (leftNode != null) { leftNode.show(); } // 在打印父结点 System.out.println(this); // 在打印右子结点 if (rightNode != null) { rightNode.show(); } } @Override public String toString() { return "TreeHeroNode{" + "id=" + id + ", name='" + name + '\'' + '}'; } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
后序遍历
后续遍历规则:
先遍历左子结点,在遍历右子结点,最后遍历父结点
效果图:

完整代码:
public static class TreeHeroNode { // 左节点 public TreeHeroNode leftNode; // 右节点 public TreeHeroNode rightNode; // 中序遍历 public void show() { // 先打印左子结点 if (leftNode != null) { leftNode.show(); } // 在打印右子结点 if (rightNode != null) { rightNode.show(); } // 最后打印父结点 System.out.println(this); } @Override public String toString() { return "TreeHeroNode{" + "id=" + id + ", name='" + name + '\'' + '}'; } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
前序,中序,后序遍历:
最重要的就是父结点
- 父结点先遍历就是前序遍历
- 父结点最后遍历就是后续遍历
- 父结点在中间就是中序遍历
层序遍历
什么是层序遍历?
上面也提到过,树是有层级别的,再来看一眼这张图:

层序遍历就是从第一层开始,依次往下,并且从左到右遍历
这张图层序遍历就是 1,3,5,12,4,8,7,6
来看看完整效果图:

看着这张图有点怪,其实这就是详细流程图!
整体思路就是通过一个队列(Queue)
- 先把root结点保存起来
- 通过一个while循环,删除当前结点
- 在删除的时候,如果左子结点或右子结点不为null,那就就添加到队列中
- 知道这个队列中没有数据证明已经遍历完成了
来看看完整代码:
# TreeHeroNode.java // 层序遍历 public void showFloor() { Queue<TreeHeroNode> queue = new LinkedList<>(); // 添加当前结点到队列中 queue.add(this); // 如果队列中一直有数据就一直循环,知道队列为null while (!queue.isEmpty()) { // 移除队列中的元素 TreeHeroNode removeNode = queue.remove(); System.out.println(removeNode); // 如果左节点不为null 就添加到队列中 if (removeNode.leftNode != null) { queue.add(removeNode.leftNode); } // 如果右节点不为null 就添加到队列中 if (removeNode.rightNode != null) { queue.add(removeNode.rightNode); } } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
走到这里4大遍历就完成了!
树的查找
前序查找
只要能看懂树的遍历,那么查找也应该就会了!
这里只以前序查找举例, 中序查找,后续查找,层序查找代码都雷同!
# TreeHeroNode.java // 树节点 public static class TreeHeroNode { public int id; public String name; // 左节点 public TreeHeroNode leftNode; // 右节点 public TreeHeroNode rightNode; /** * 前序查找 * @param valueID: 需要查找的ID */ public TreeHeroNode findValue(int valueID) { System.out.println(this); TreeHeroNode resultTemp = null; // 如果当前id和查找的id相同,这直接返回当前对象 if (id == valueID) { return this; } // 查找左侧 if (leftNode != null) { resultTemp = leftNode.findValue(valueID); } // 如果在查找左子树的过程中找到了那么就直接结束 if(resultTemp != null){ return resultTemp; } // 查找右子树 if (rightNode != null) { resultTemp = rightNode.findValue(valueID); } // 查找完右子树直接返回 // 如果是null 说明没有找到 return resultTemp; } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
树的删除
前序删除
删除结点和查找结点不同
因为要删除的结点可能是
- 子树
- 叶子结点
- 左子 / 右子结点
假设删除的是子树,那么目前就让整颗子树删除,例如这样:
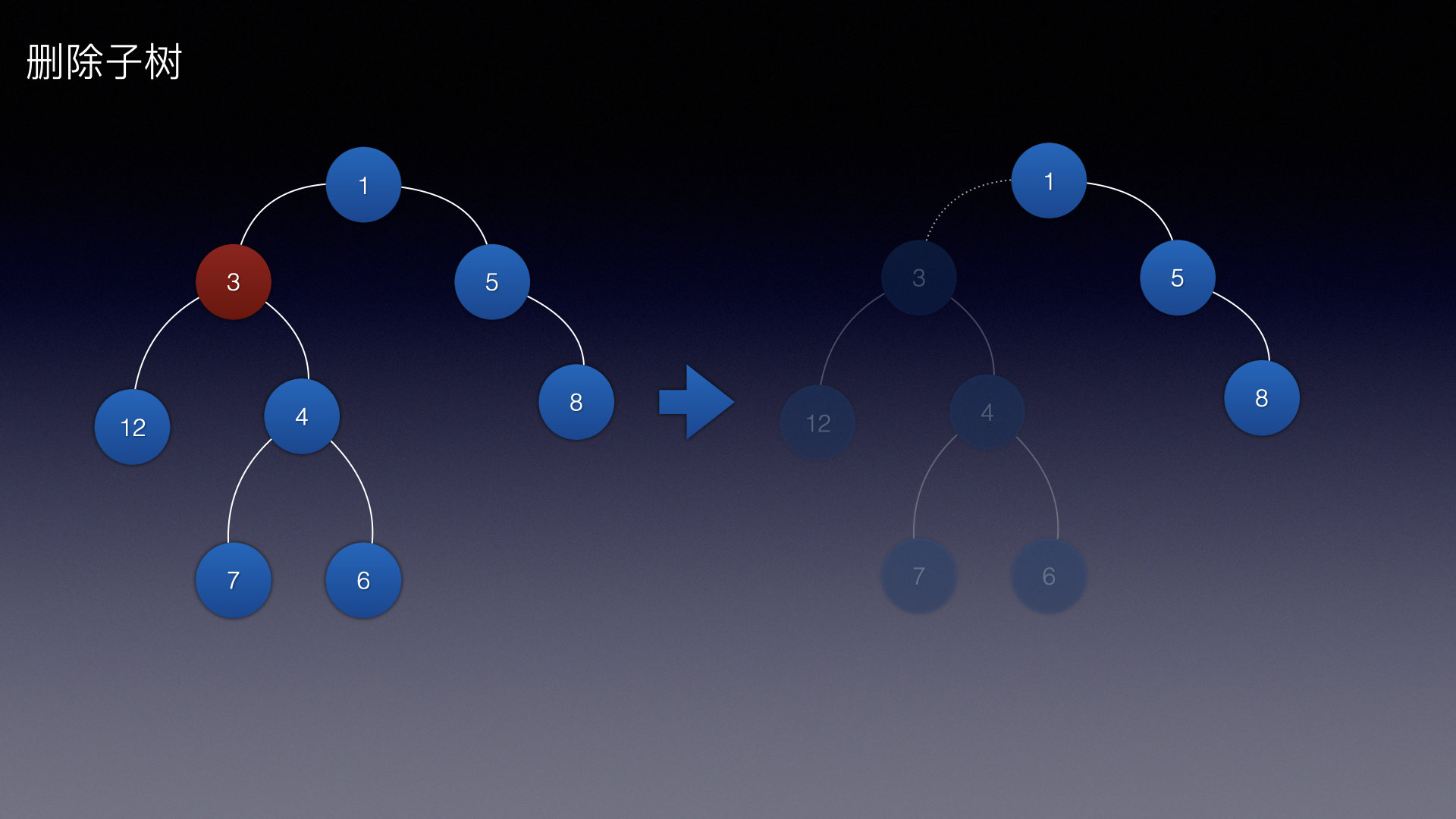
那么删除一个叶子结点就是这样:
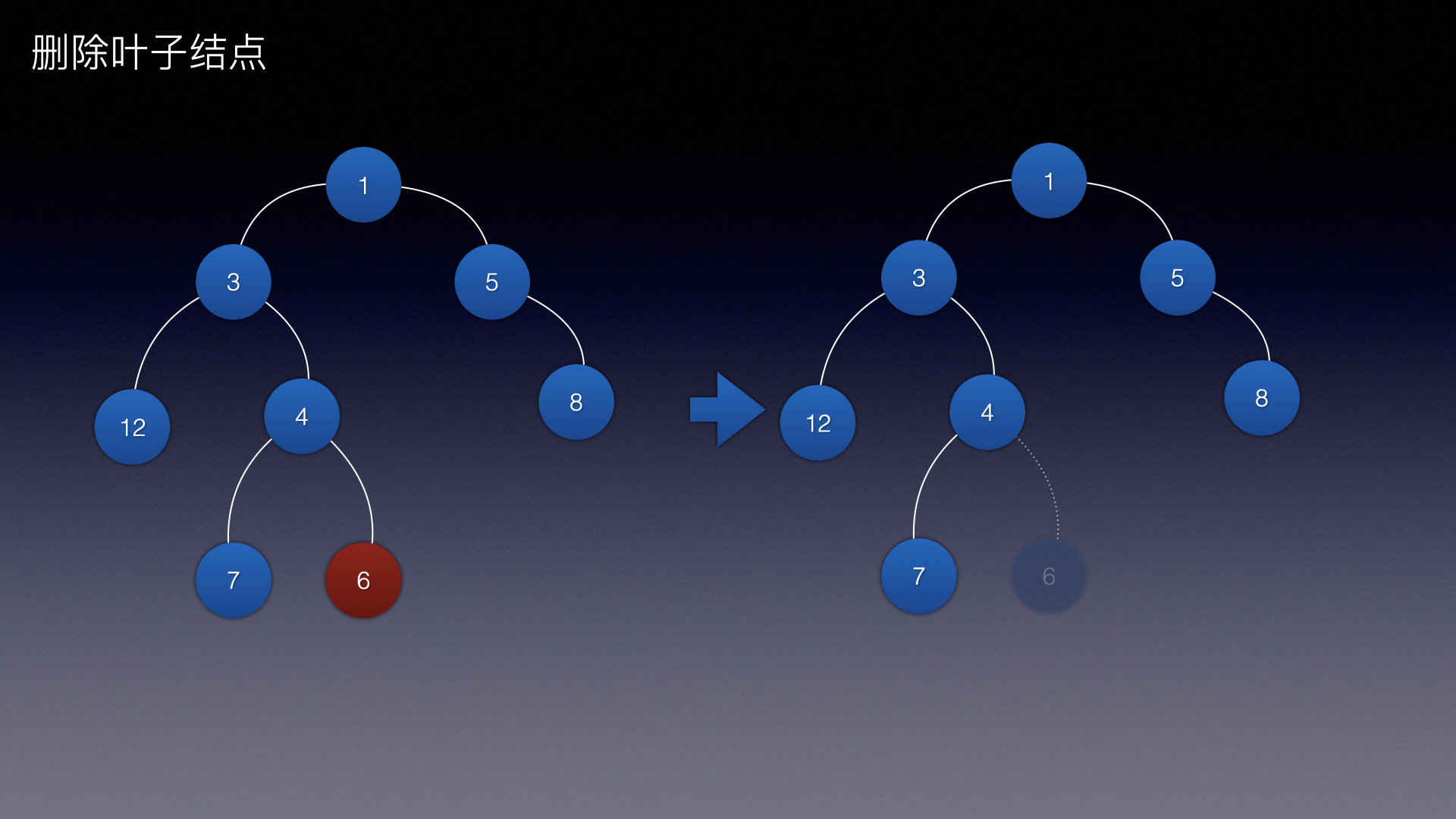
整体思路:
- 首先得会前序遍历
- 然后在遍历的过程中,如果找到了要删除的结点
- 先要看一下他是左子结点 还是右子结点
- 如果是左子结点,那么就让他左子结点 = null 即可
- 如果是右子结点,那么就让他右子结点 = null 即可
来看看完整代码:
// 树节点 public static class TreeHeroNode { public int id; public String name; // 左节点 public TreeHeroNode leftNode; // 右节点 public TreeHeroNode rightNode; public TreeHeroNode removeID(int valueID) { TreeHeroNode resultTemp; // 前序删除 if (id == valueID) { return this; } // 左子节点 != null 就递归查找 if (leftNode != null) { resultTemp = leftNode.removeID(valueID); // 如果找到了当前左节点,那么让当前左节点置空即可 if (resultTemp != null) { leftNode = null; } } // 查找右子节点 if (rightNode != null) { resultTemp = rightNode.removeID( valueID); // resultTemp != null 表示找到了右子节点,将节点置空即可 if (resultTemp != null) { rightNode = null; } } return null; } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
在后面的系列中,会讲解如何删除一个结点就删除一个结点,而不是删除整颗树的! 不要心急,耐心期待吧~~
原创不易,您的点赞就是对我最大的支持!
下一篇:顺序二叉树[开发中…]
-
相关阅读:
uboot模式下通过tftp移植内核遇到的问题
猿创征文|【JavaSE】 Collection集合全家桶
LLMs 规模化人类反馈Scaling human feedback
R生成三线表
常见的十种排序算法C++实现(附时空复杂度,稳定性分析)
sqlite条件查询语句where
第五十五天 P1036 [NOIP2002 普及组] 选数
利用PaddleDetection 训练自定义COCO数据集进行目标检测
Vue实现顶部滚动条
信创办公–基于WPS的EXCEL最佳实践系列 (单元格与行列)
- 原文地址:https://blog.csdn.net/weixin_44819566/article/details/125487596