算法原理

  上述的排列树算法虽然也适用于全排列。但是全排列有更好的算法，这个算法就是大名鼎鼎的Heap算法Heap’s algorithm。注意，这里的Heap不是堆的意思，而是计算机科学家B. R. Heap的姓氏。
  Heap算法是一种递归算法。他的想法就是用互换生成整个凯莱图。其基本算法是这样的，先把前n-1项使用递归方法去互换。一系列互换完成，再与最后一个元素互换。具体的置换原理非常难，网上没有讲清楚的，我这次多用几张图画清楚吧，以ABC三个元素的排列，先看看位置变化：

  上面的图什么意思呢？在减号前面是进入节点时的排列，减号后面是程序流程离开节点后的排列。
  这很难看出规律，如果知道置换知识可能更容易理解。我们改成置换表达式再看看：

  在置换图里，因为下层递归完成后，会再执行一次置换，而这次置换会影响同级的下一个节点，所以我把置换放入了平级箭头上。因为最后还执行了一次(1 3)，所以我画了一个指向根节点的箭头。我们知道对于3个元素的置换，(1 2)与(1 3)交替就可以遍历完，这在凯莱图里是一个六边形。三元素的置换不足以剖析Heap算法的精妙之处。
  因为三元素的置换，会让人误以为，每个元素和最后一个元素交换就行了。但是事实不是这样，起码两个元素的交换不是这样，比如最底层的$(12)$后面没有再进行一个$(12)$置换。下面这幅图是四个元素的全排列：

  接下来我重点讲讲为什么奇偶处理不一样。如果把四元素的置换换成四个左陪集效果会更明显：

  而大循环的起点是这样的：

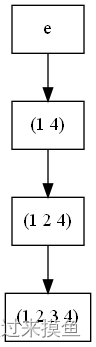
  对于n为偶数的对称群$S_n$来说，有这么一个规律：其子群$S_{n-1}$的每个左陪集里有$e,(1n),(12n),(123n),\dots ,(123\dots n)$这些元素。注意，偶数不会还原为恒等置换e,会残留一个$(123\dots n)$这样的置换。那么如果放到更大的循环，例如进行五元素的排列，又会如何呢？看下图：
  对于奇数来说而每个偶数的递归子程序会残留一个$(123\dots n-1)$，与奇数的$(1n)$恰好组成$(123\dots n)$置换，而n个$(123\dots n)$恰好变回恒等置换e。例如上图的$(1234)$与$(15)$组成$(12345)$，五个$(12345)$恰好还原为e。所以Heap算法的核心原理就是偶数残留一个全错位置换($(123\dots n)$)，奇数再还原为e。这样一奇一偶，循环往复，其代码思想十分优美。

Python实现

def recursive(array, last, result):
    if last == 0:
        result.append(array[:])
        return

    for i in range(0, last + 1):
        recursive(array, last - 1, result)
        before = array[:]
        if last & 1 == 0:
            array[0], array[last] = array[last], array[0]
        else:
            array[i], array[last] = array[last], array[i]


def permutations(array):
    result = []
    recursive(array, len(array) - 1, result)
    return result


if __name__ == '__main__':
    result = permutations(['A', 'B', 'C', 'D'])
    for x in result:
        print(x)


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

  测试结果：

['A', 'B', 'C', 'D']
['B', 'A', 'C', 'D']
['C', 'A', 'B', 'D']
['A', 'C', 'B', 'D']
['B', 'C', 'A', 'D']
['C', 'B', 'A', 'D']
['D', 'B', 'C', 'A']
['B', 'D', 'C', 'A']
['C', 'D', 'B', 'A']
['D', 'C', 'B', 'A']
['B', 'C', 'D', 'A']
['C', 'B', 'D', 'A']
['D', 'A', 'C', 'B']
['A', 'D', 'C', 'B']
['C', 'D', 'A', 'B']
['D', 'C', 'A', 'B']
['A', 'C', 'D', 'B']
['C', 'A', 'D', 'B']
['D', 'A', 'B', 'C']
['A', 'D', 'B', 'C']
['B', 'D', 'A', 'C']
['D', 'B', 'A', 'C']
['A', 'B', 'D', 'C']
['B', 'A', 'D', 'C']
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24