-
[英雄星球六月集训LeetCode解题日报] 第27日 图
[英雄星球六月集训LeetCode解题日报] 第27日 图
日报
- 今天三道搜索题,比较套路,简单处理即可。
题目
一、 1514. 概率最大的路径
链接: 1514. 概率最大的路径
1. 题目描述
- 概率最大的路径
难度:中等
给你一个由
n个节点(下标从 0 开始)组成的无向加权图,该图由一个描述边的列表组成,其中edges[i] = [a, b]表示连接节点 a 和 b 的一条无向边,且该边遍历成功的概率为succProb[i]。指定两个节点分别作为起点
start和终点end,请你找出从起点到终点成功概率最大的路径,并返回其成功概率。如果不存在从
start到end的路径,请 返回 0 。只要答案与标准答案的误差不超过 **1e-5 **,就会被视作正确答案。示例 1:

输入:n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start = 0, end = 2 输出:0.25000 解释:从起点到终点有两条路径,其中一条的成功概率为 0.2 ,而另一条为 0.5 * 0.5 = 0.25- 1
- 2
- 3
- 4
示例 2:
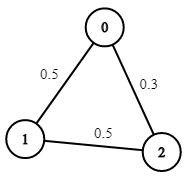
输入:n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.3], start = 0, end = 2 输出:0.30000- 1
- 2
- 3
示例 3:

输入:n = 3, edges = [[0,1]], succProb = [0.5], start = 0, end = 2 输出:0.00000 解释:节点 0 和 节点 2 之间不存在路径- 1
- 2
- 3
- 4
提示:
2 <= n <= 10^40 <= start, end < nstart != end0 <= a, b < na != b0 <= succProb.length == edges.length <= 2*10^40 <= succProb[i] <= 1- 每两个节点之间最多有一条边
2. 思路分析
- 首先想到最短路,发现这题的权重是成功概率,而每经过一条边,成功概率明显是下降的。
- 因此转化为求失败概率,最后1减即可。
- 注意节点松弛时,不是加法,两个失败概率求总失败概率,走calc,具体看代码。
- 用Dijkstra,CV成功!
3. 代码实现
Djikstraclass Solution: def maxProbability(self, n: int, edges: List[List[int]], succProb: List[float], start: int, end: int) -> float: graph = defaultdict(dict) for i in range(len(edges)): a,b = edges[i] p = succProb[i] graph[a][b] = 1-p graph[b][a] = 1-p def calc(p1,p2): return 1-(1-p1)*(1-p2) def dijkstra(graph,start): from queue import PriorityQueue dist = collections.defaultdict(lambda:1.0) # 初始化距离数组 dist[start] = 0 # 原点到自己是0 visited = set([start]) # 访问过原点了 q = PriorityQueue() for v,w in graph[start].items(): # 找到所有原点的邻居,更新他们的dist dist[v] = w q.put((w,v)) # 权放前边,注意是put while not q.empty(): x,u = q.get() # 用u给别的节点做松弛,注意是get if u in visited: continue visited.add(u) for v,w in graph[u].items(): new_dist = calc(dist[u],w) if new_dist < dist[v]: dist[v] = new_dist if v not in visited: q.put((new_dist,v)) return dist dist = dijkstra(graph,start) return 1-dist[end]- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
二、 LCP 56. 信物传送
链接: LCP 56. 信物传送
1. 题目描述

2. 思路分析
这题我们要求的是最少操作次数,而每个块都可以操作,因此实际的状态转移依然是四个防线,遍历是否操作即可。
- 因此我们需要用优先队列来储存,优先处理操作次数少的状态。
- 状态转移时,如果这个状态之前储存的操作次数大于本次计算的,那么更新为更小次数,重新转移。
- 剩下的就是裸BFS最短路径。
3. 代码实现
class Solution: def conveyorBelt(self, matrix: List[str], start: List[int], end: List[int]) -> int: m,n = len(matrix),len(matrix[0]) end = (end[0],end[1]) visited = {(start[0],start[1]):0} q = [(0,start[0],start[1])] def in_bound(x,y): return 0<=x<m and 0<=y<n dirs = [ (0,1), (0,-1), (1,0), (-1,0) ] while q: change,i,j = heapq.heappop(q) if (i,j) == end: return change # print(change,i,j) cur = matrix[i][j] for a,b in dirs: x,y = i+a,j+b new_change = change+1 if cur == '>' and (a,b) == (0,1): new_change -= 1 elif cur == '<' and (a,b) == (0,-1): new_change -= 1 elif cur == '^' and (a,b) == (-1,0): new_change -= 1 elif cur == 'v' and (a,b) == (1,0): new_change -= 1 # if (x,y) == end: # return new_change if in_bound(x,y) and ((x,y) not in visited or visited[(x,y)]>new_change): visited[(x,y)] = new_change heapq.heappush(q,(new_change,x,y)) return -1- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
三、 1377. T 秒后青蛙的位置
链接: 1377. T 秒后青蛙的位置
1. 题目描述
- T 秒后青蛙的位置
难度:困难
给你一棵由 n 个顶点组成的无向树,顶点编号从 1 到
n。青蛙从 顶点 1 开始起跳。规则如下:- 在一秒内,青蛙从它所在的当前顶点跳到另一个 未访问 过的顶点(如果它们直接相连)。
- 青蛙无法跳回已经访问过的顶点。
- 如果青蛙可以跳到多个不同顶点,那么它跳到其中任意一个顶点上的机率都相同。
- 如果青蛙不能跳到任何未访问过的顶点上,那么它每次跳跃都会停留在原地。
无向树的边用数组
edges描述,其中edges[i] = [fromi, toi]意味着存在一条直接连通fromi和toi两个顶点的边。返回青蛙在
t秒后位于目标顶点target上的概率。示例 1:

输入:n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 2, target = 4 输出:0.16666666666666666 解释:上图显示了青蛙的跳跃路径。青蛙从顶点 1 起跳,第 1 秒 有 1/3 的概率跳到顶点 2 ,然后第 2 秒 有 1/2 的概率跳到顶点 4,因此青蛙在 2 秒后位于顶点 4 的概率是 1/3 * 1/2 = 1/6 = 0.16666666666666666 。- 1
- 2
- 3
- 4
示例 2:

输入:n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 1, target = 7 输出:0.3333333333333333 解释:上图显示了青蛙的跳跃路径。青蛙从顶点 1 起跳,有 1/3 = 0.3333333333333333 的概率能够 1 秒 后跳到顶点 7 。- 1
- 2
- 3
- 4
提示:
1 <= n <= 100edges.length == n - 1edges[i].length == 21 <= ai, bi <= n1 <= t <= 501 <= target <= n
2. 思路分析
这题看似吓人,地铁上想了一会其实就是要分类讨论。
- 这题给出的图是树,回顾一下这题用到的树的性质:
- 节点数=边树+1。
- 每两个节点都有一条唯一路径联通。
- 无环。
- 青蛙每一秒都必须跳一下,不能往回跳,因此我们层先法遍历即可,每个位置的访问时间就是步数。
- 除非这个位置是叶子节点,不能继续跳了,否则它在以后的时间不会再回来。
- 那么就很简单了。
- 层先遍历,每次计算当前节点当前时间的概率。
- 如果遍历完第t层,还没遇到target:说明时间t不足以到达target,return 0
- 如果遇到target的时间是t1,概率p:
- t == t1:return p
- t>t1:
- 没有后续节点,那么以后也不会走了,后续节点不会影响这个位置,因此t时target概率就是p;
- 若有后续节点,那么就走了,不会回来,return 0
- 注意我们处理的是nxt,不会处理到根,因此要特殊处理根节点。
- 如果目标是根(1):
- 若t==0,则return 1
- 若t>0,只有根没有子节点才return 1;否则一定走了不会回来return 0。
- 如果目标是根(1):
3. 代码实现
class Solution: def frogPosition(self, n: int, edges: List[List[int]], t: int, target: int) -> float: graph = defaultdict(list) for u,v in edges: graph[u].append(v) graph[v].append(u) if target == 1: if t == 0: return 1.0 else: if len(graph[1])==0: return 1 else: return 0 visited = {1:1.0} q = deque(visited) step = 0 while q: new_q = deque() step += 1 while q: cur = q.popleft() sel = len(graph[cur]) - 1 if cur != 1 else len(graph[cur]) # 下一步能取的位置数,减去父节点。 p = visited[cur] # x 本身带的概率 if sel == 0: continue new_p = p*(1/sel) for nxt in graph[cur]: if nxt in visited: continue if nxt == target : if t == step: return new_p else: if len(graph[nxt]) == 1: return new_p else: return 0.0 visited[nxt] = new_p new_q.append(nxt) if step == t: return 0.0 q = new_q return 0- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
-
相关阅读:
SpringMVC学习
docker 安装wazuh遇到的问题
Leetcode 算法面试冲刺 热题 HOT 100 刷题(406 416 437 438 448)(六十九)
在读取xlsx文件写入数据库的时候发现了这种问题
day17-高速缓冲区的管理机制
使用了百度OCR,记录一下
探索式测试的谬论
自旋锁探秘
python中强制关闭线程、协程、进程方法
JAVA高级(二)
- 原文地址:https://blog.csdn.net/liuliangcan/article/details/125481548
