西电数据挖掘实验3——复杂网络社团检测

一、实验内容

  复杂网络是描述复杂系统的有力工具，其中每个实体定义成一个节点，实体间的交互关系定义为边。复杂网络社团结构定义为内紧外松的拓扑结构，即一组节点的集合，集合内的节点交互紧密，与外界节点交互松散。复杂网络社团结构检测广泛的应用于信息推荐系统、致癌基因识别、数据挖掘等领域。

  本实验利用两类数据：模拟数据与真实数据。模拟数据有著名复杂网络学者Mark Newmann所提出，该网络包括128个节点，每个节点的度为16，网络包含4个社团结构，每个社团包含32个节点，每个节点与社团内部节点有$k_1$个节点相互链接，与社团外部有$k_2$个节点相互链接 （$k_1+k_2=16$）。通过调节参数$k_2$（$k_2=1,2,...,8$）增加社团构建检测难度。

  真实数据集：跆拳道俱乐部数据由34个节点组成，由于管理上的分歧，俱乐部分解成两个社团。

二、分析及设计

  Step1：导入网络数据

  利用邻接矩阵$A$来存储网络，其中$A_{ij}$表示第$i$个节点与第$j$个节点的是否有边相互链接，1表示有，0表示没有。

  在本次实验中，我利用Python中的networkx包处理网络数据。networkx能够有效地组织与管理图数据结构，并且其中封装了很多与图操作相关的函数调用，能够提高本次实验程序的编写效率。

  Step2：根据网络结构特征给出节点相似性度量指标

  给定节点$i$, 其邻居节点定义为与该节点相链接的所有节点组成的集合，即 N ( i ) = { j ∣ A i j = 1 , j = 1 , 2 , . . . , n } N(i)=\{j|A_{ij}=1,j=1,2,...,n\} N(i)={j∣Aij​=1,j=1,2,...,n}。给定一对节点$(i,j)$，其相似性定义如下：
$$S_{ij}=\frac{|N(i)\cap N(j)|}{|N(i)\cup N(j)|}$$
其中$|N(i)\cap N(j)|$表示集合$N(i)\cap N(j)$中元素的个数。

  Step3：采用贪婪算法提取模块

  随机选择一个未聚类的节点作为当前社团C，提取出社团C所有未聚类的邻居节点$N(c)$。选择使得社团密度降低最小的那个节点$v$添加到社团$C$，更新当前社团为$C=C\cup v$（若某节点已经找不到其未聚类的邻居节点，则认为该节点自成一个社团），持续该过程直到当前社团的密度小于某个阈值。当一个社团提取完成后，将其加入存放总社团的集合中，即$Clubs=Clubs\cup C$。此后，再从剩余的未被分类的节点中任选一个出来作为新社团的初始节点，重复进行上述操作，直到所有节点均被归类到某一社团中，算法结束。计算过程中我使用社团中所有节点对的相似度之和除以节点对总数(组合数)再除以2来定义的社团密度，具体函数表达式如下：
$$Density=\frac{{\sum }_{i,j}{s}_{ij}}{C_{len(c)}^2/2}\in (0,2)$$
其中$len(c)$是社团$c$中的节点个数，$C_{len(c)}^2$是从社团$c$的节点中任选2个节点的组合数，$i,j$是从$c$中任取2个节点的组合对应的节点标号。

  Step4：采用Cytoscape工具，可视化聚类结果

  由于Cytoscape对于被导入的文件中的数据格式有一定的要求，所以我先用Python对karate.gml中的数据进行了处理，输出了符合Cytoscape导入数据规范的边数据，然后再将边数据导入txt文件中，最后导入Cytoscape。导入Cytoscape后，根据Python计算出的社团分类结果，将这34个节点分别着色，每个社团中的节点着同色，最终完成可视化操作。

三、详细实现

  由于本次实验需要处理图数据，对图中节点进行相关操作，而Python中有很强大的networkx包便于我们构建和操作复杂的图结构，故我选择用Python编写本次实验的程序。具体代码实现如下（所有重要语句均已给出相应的注释）：

1.先导入本实验需要用到的包：

import random
import copy
import numpy as np
import networkx as nx
import matplotlib.pyplot as plt
1
2
3
4
5

2.定义函数show_info()，显示一下社团网络的相关信息：

# 显示图G的相关信息
def show_info(G):
    # 输出所有节点和所有边
    print("nodes:", G.nodes(), '\n')
    print("edges:", G.edges(), '\n')
    # 输出节点总数和边总数
    nodes_num = G.number_of_nodes()
    edges_num = G.number_of_edges()
    print("number of nodes:", nodes_num)
    print("number of edges:", edges_num)
1
2
3
4
5
6
7
8
9
10

3.定义函数clac_s()，利用题目中给出的相似性计算公式计算相似性矩阵：

# 计算相似性矩阵
def calc_s(G):
    # 初始化s
    nodes_num = G.number_of_nodes()
    sim = np.zeros((nodes_num,nodes_num))
    # 开始计算s
    for i in range(1, nodes_num + 1):
        for j in range(1, nodes_num + 1):
            # 根据定义计算i,j的相似性
            sim[i-1][j-1] = len(G.adj[i].keys() & G.adj[j].keys()) / len(G.adj[i].keys() | G.adj[j].keys())
    print('图G的相似性矩阵为：')
    print(sim)
    return sim
1
2
3
4
5
6
7
8
9
10
11
12
13

4.定义函数calc_density()计算社团密度：

# 计算社团密度（采用基于相似度度量的密度）
def calc_density(c, s):
    # 求出社团中的点数和边数
    v = c.number_of_nodes()
    e = c.number_of_edges()
    # 若社团中只有一个点，则密度最大，为1
    if len(c) == 1:
        return 1.0
    # 初始化总相似度
    sum_sim = 0.0
    for node_i in list(c.nodes()):
        for node_j in list(c.nodes()):
            # 不计算自身
            if (node_i != node_j) & (node_j.__index__() > node_i.__index__()):
                sum_sim = sum_sim + s[node_i-1][node_j-1]
    # 最后除以社团c中node_i,node_j的组合数再除以系数
    density_2 = sum_sim / ( ( v * (v - 1) ) / 4 )
    # 最后返回社团密度
    return density_2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

5.定义函数find_nbrs()求出社团所有未聚类的邻居节点：

# 求社团未聚类的邻居节点
def find_nbrs(G, G_copy, c):
    # 初始化
    nbrs = []
    for node in list(c.nodes()):
        # node的邻居应该在G中找
        node_nbrs = list(G.adj[node].keys())
        nbrs = list(set(nbrs) | (set(node_nbrs)))
    # 未聚类的邻居节点应该在G_copy中找，最后以数值形式存放在列表里
    final_nbrs = list(set(nbrs) & (set(list(G_copy.nodes()))))
    return final_nbrs
1
2
3
4
5
6
7
8
9
10
11

6.定义核心函数club_julei()利用贪心算法求解所有社团，算法思想在上文中已经阐述，算法细节见注释：

# 这里是初始化全局变量picked_node
picked_node = 0
# 利用贪心算法找到所有的社团——核心函数
def club_julei(G, s, t):
    # 初始化列表存放所有社团列表
    clubs = []
    # 深拷贝G，否则对G_copy操作也会同时影响G
    G_copy = copy.deepcopy(G)
    # 当G_copy的节点列表不为空时循环寻找社团，G_copy节点列表为空时说明所有的社团均已被找到
    while(G_copy.nodes()):
        # 注意列表下标从0开始
        c = nx.Graph()
        idx = random.randint(0, len(G_copy)-1)
        # 随机选择一个G_copy中的节点初始化社团c（G_copy中节点都是未被聚类的）
        randpick_node = list(G_copy.nodes())[idx]
        c.add_node(randpick_node)
        # 从G_copy中删去该节点
        G_copy.remove_node(randpick_node)
        # 死循环构造社团直到社团密度小于阈值
        while(1):
            # 计算原始社团密度
            density_old = calc_density(c, s)
            # 求当前社团未聚类的邻居节点
            candinodes = find_nbrs(G, G_copy, c)
            if len(candinodes) == 0:
                clubs.append(list(c.nodes()))
                break
            minval = 1.0
            global picked_node # 全局变量picked_node 
            # 寻找使社团密度降低最小的那个节点
            for node in candinodes:
                c.add_node(node)
                # 计算加入该节点后的社团密度
                density_new = calc_density(c, s)
                # 计算社团密度减小量
                dec = density_old - density_new
                # 若dec<minval，更新数据
                if dec < minval:
                    minval = dec
                    picked_node = node
                # 测试完当前结点后删除该节点，再循环测下一个
                c.remove_node(node)
            # 循环结束后picked_node已找到，将该节点加入社团c
            # 这里判断是否为0是为了应对picked_node未被赋值的情况
            if picked_node == 0:
                continue
            else:
                c.add_node(picked_node)
            # 同时在G中删除该点，因为该点已被分类
            if picked_node in list(G_copy.nodes()):
                G_copy.remove_node(picked_node)
            # 若当前社团的密度小于阈值，则将其加入到clubs列表中
            if calc_density(c, s) < t:
                #print(calc_density(c, s))
                clubs.append(list(c.nodes()))
                break
    # 返回所有社团
    return clubs
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

四、实验结果

 社团聚类结果随着社团密度阈值选取的不同（0.2, 0.4, 0.5）而变化的情况如下图所示：

 我用Cytoscape绘制了阈值t分别取0.2，0.4，0.5时的社团聚类结果图（其余阈值下画法类似，不再展示结果），效果如下：

 t = 0.2时的社团聚类结果：

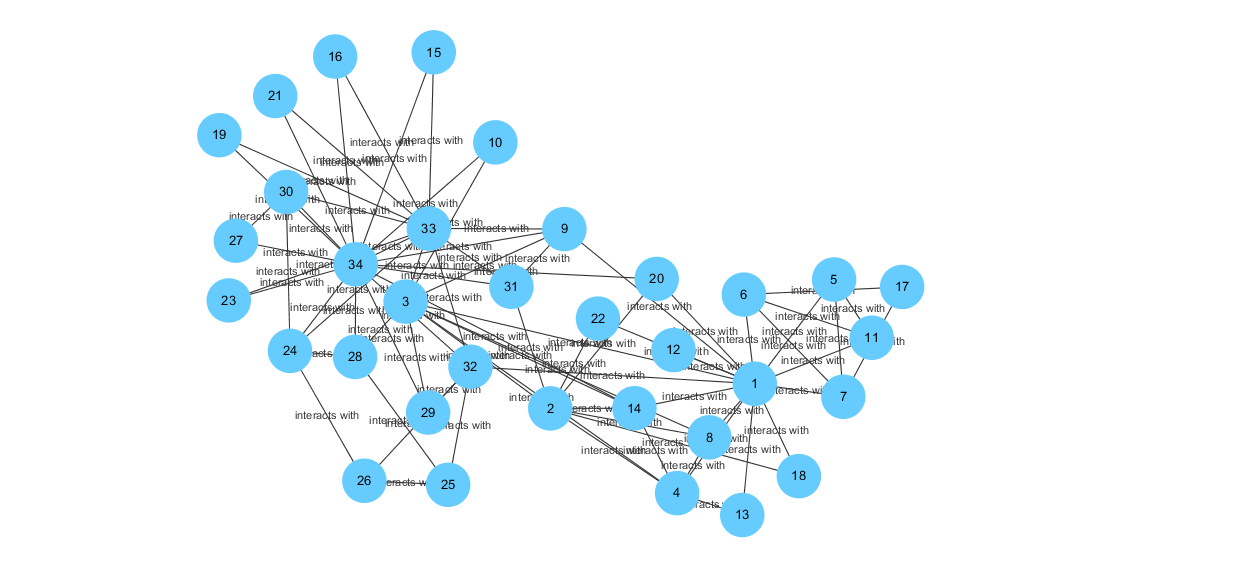
 t = 0.4时的社团聚类结果：

 t = 0.5时的社团聚类结果：

  分析上图可知，当阈值t = 0.4左右时，社团聚类的效果最好。当密度阈值设定为一个比较小的数时（如小于0.1），所有节点被分到同一个社团中；当密度阈值稍微增大后（如0.2-0.5），将会出现更多的社团，当密度阈值取到比较大的值后（如大于0.6），基本上一个社团中只存在两三个节点。当然，即使在同一阈值下，每次运行程序得到的社团聚类结果也是不同的，这是因为每次随机选取的初始节点不同，最终合成的社团也会不同。

  在实验中，我尝试过用基本的图密度定义：$density=\frac{2|E|}{|V|\cdot |V-1|}$去计算社团的密度，也尝试过用图密度+基于相似性的密度去计算社团密度，但是后来发现这两种方法划分社团的效果并不理想，具体表现为当阈值还不是很大（如0.4）时就已经划分出很多小社团了，不符合我们的预期。