从入门开始手把手搭建千万级Java算法测试-快速化排序与随机化查找第k大数

  第十天开始呢，我们开始讲解快速化排序与随机化查找第k大数，从算法思路，到算法伪代码实现，到复杂度分析，从这里开始我们手把手搭建一个测试平台的基础，根据你自身硬件水平可以对下列代码进行从1000，到千万级测试，其中算法测试时间与你的机器硬件水平和实现的算法有关系，下面是快速化排序与随机化查找第k大数算法具体讲解。

（1）排序算法的思路

  传统的查找第k大数是基本思路：求n个元素当中第k小的元素采用分置的思想，即取一确定数v，顺次比较n个数与该确定数的大小，将小于该数的存入数组A1，等于该数的存入数组A2，大于该数的存入数组A3；

  快速排序基本思想：选择一个基准数，通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小。然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以达到全部数据变成有序。

（2）算法伪代码

//随机化方法择第k小元素算法伪代码
RSelect(Integer[] a, int low, long hight, long k) {
        for(int i=0;i<a.length;i++){
            if(a[i]<x)
                a1.add(a[i]);
            if(a[i]==x)
                a2.add(a[i]);
            if(a[i]>x)
                a3.add(a[i]);
        }
        if(a1.size() >= k){
            Integer[] a11 = new Integer[a1.size()];
            for(int i=0;i<a1.size();i++){
                a11[i] = a1.get(i);
            }
            return RSelect(a11, 1, a11.length, k);
        }
        if(a1.size()+a2.size() >= k){
            return x;
        }
        if(a1.size()+a2.size()+a3.size() >= k){
            Integer[] a31 = new Integer[a3.size()];
            for(int i=0;i<a3.size();i++){
                a31[i] = a3.get(i);
            }
            return RSelect(a31, 1, a31.length, k-a1.size()-a2.size());
        }
    }
//快速排序算法伪代码
QuickSort(A,left,right):{
   if right<left:
      return   
   m <- Partition(A,left,right)
   QuickSort(A,left, m-1)
   QuickSort(A,m+1,right)
}
Change(A,left,right):{//使用固定位置数
   x <- A[left]
   lower_bound <- left
   greater_bound <- right
   for i from left+1 to right:
      if A[i] <= A[left]:
          swap(A[lower_bound+1],A[i])
          lower_bound <- i+1
   swap(A[lower_bound],A[left])
}



1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

（3）复杂度分析

1.随机化方法择第k小元素算法
  比较k与三个数组的长度，若|A1|>=k，则重复上过程；若|A1|+|A2|>=k，则返回该确定数（即44）；若|A1|+|A2|<k，则重复上过程，此时求A3数组当中第k-|A1|-|A2|小的元素。
  时间复杂度的期望比较次数C(n) ≤4n，此外每个元素与基准元素x至少比较一次。故C(n) ≥n及n≤C(n)≤4n,故时间复杂度为Θ（n）。

（2）快速排序算法
  在最优情况下，Partition每次都划分得很均匀，如果排序n个关键字,其递归树的深度就为.log2n.+1（.x.表示不大于x的最大整数），即仅需递归log2n次，需要时间为T（n）的话
  第一次Partiation应该是需要对整个数组扫描一遍，做n次比较。然后，获得的枢轴将数组一分为二，那么各自还需要T（n/2）的时间（注意是最好情况，所以平分两半）。
于是不断地划分下去，我们就有了下面的不等式推断。
T（n）≤2T（n/2） +n，T（1）=0
T（n）≤2（2T（n/4）+n/2） +n=4T（n/4）+2n
T（n）≤4（2T（n/8）+n/4） +2n=8T（n/8）+3n
……
T（n）≤nT（1）+（log2n）×n= O(nlogn)
由数学归纳法可证明，其数量级为O(nlogn)。
空间复杂度来说，主要是递归造成的栈空间的使用，最好情况，递归树的深  度为log2n，其空间复杂度也就为O(logn)，最坏情况，需要进行n‐1递归调用，其空间复杂度为O(n)，平均情况，空间复杂度也为O(logn)
  由于关键字的比较和交换是跳跃进行的，因此，快速排序是一种不稳定的排序方法。

（4）代码主体部分

package runoob;

import java.util.ArrayList;
import java.util.Random;
import java.util.Scanner;


public class RandomSelect {
    public int RSelect(Integer[] a, int low, long hight, long k) {
        Random random = new Random();
        int v = random.nextInt(Math.toIntExact(hight - 1 - low - 1 + 1))+low;
        int x = a[v];
        
        ArrayList<Integer> a1 = new ArrayList<>();
        ArrayList<Integer> a2 = new ArrayList<>();
        ArrayList<Integer> a3 = new ArrayList<>();

        for(int i=0;i<a.length;i++){
            if(a[i]<x)
                a1.add(a[i]);
            if(a[i]==x)
                a2.add(a[i]);
            if(a[i]>x)
                a3.add(a[i]);
        }

        if(a1.size() >= k){
            Integer[] mid = new Integer[a1.size()];
            for(int i=0;i<a1.size();i++){
                mid[i] = a1.get(i);
            }
            return RSelect(mid, 1, mid.length, k);
        }

        if(a1.size()+a2.size() >= k){
            return x;
        }

        if(a1.size()+a2.size()+a3.size() >= k){
            Integer[] mid = new Integer[a3.size()];
            for(int i=0;i<a3.size();i++){
                mid[i] = a3.get(i);
            }
            return RSelect(mid, 1, mid.length, k-a1.size()-a2.size());
        }

        else
            return 0;
    }

    public static void RoandomSelect_text(long num) {
        Integer[] arr = SortHelper.generateRandomArray(num, 0, 1000);
        Scanner scanner = new Scanner(System.in);
        RandomSelect R=new RandomSelect();
        Quick_sort Q=new Quick_sort();
        long k;

        System.out.println("请输入查找第k的位置");
        k = scanner.nextInt();

        long start = System.nanoTime();
        Q.sort(arr, 0, arr.length - 1);
        long mid = System.nanoTime();
        long knum = R.RSelect(arr, 0, num + 1, k);
        long end = System.nanoTime();

        System.out.println("快速化排序花费时间:" + (mid - start)/1000 + "(ms)");
        System.out.println("随机化查找第k个数花费时间:" + (end - mid)/1000 + "(ms)");
        System.out.println("计算机1901谢威找到第" + k + "个数为"+knum);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71

  对应代码中的SortHelper类我们留一个小小的悬念，留到最后来进行叙说，其中目前来说他的方法generateRandomArray的参数为，（num，left，right）第一个参数参与算法生成的数量级，作为随机生成序列，它可以为千万，因为是long级别，left和right则为生成序列的大小范围，生成的序列为返回值类型为Integer[]。
（5）测试结果如下：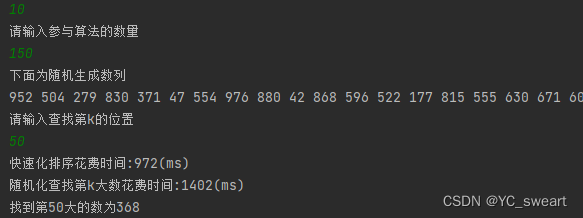

  笔者有兴趣可以尝试千万级的算法测试，这里便不在赘述。