[LeetCode周赛复盘] 第 81 场双周赛20220625

一、本周周赛总结

• 第一次参加双周赛，真是惨不忍睹。
• 我真是菜到不行。
  

二、 [Easy] 6104. 统计星号

链接: 6104. 统计星号

1. 题目描述

6104. 统计星号

难度：简单

给你一个字符串 s ，每 两个 连续竖线 ‘|’ 为 一对 。换言之，第一个和第二个 ‘|’ 为一对，第三个和第四个 ‘|’ 为一对，以此类推。

请你返回 不在 竖线对之间，s 中 ‘*’ 的数目。

注意，每个竖线 ‘|’ 都会 恰好 属于一个对。

示例 1：

输入：s = "l|*e*et|c**o|*de|"
输出：2
解释：不在竖线对之间的字符加粗加斜体后，得到字符串："l|*e*et|c**o|*de|" 。
第一和第二条竖线 '|' 之间的字符不计入答案。
同时，第三条和第四条竖线 '|' 之间的字符也不计入答案。
不在竖线对之间总共有 2 个星号，所以我们返回 2 。
1
2
3
4
5
6

示例 2：

输入：s = "iamprogrammer"
输出：0
解释：在这个例子中，s 中没有星号。所以返回 0 。

1
2
3
4

示例 3：

输入：s = "yo|uar|e**|b|e***au|tifu|l"
输出：5
解释：需要考虑的字符加粗加斜体后："yo|uar|e**|b|e***au|tifu|l" 。不在竖线对之间总共有 5 个星号。所以我们返回 5 。
1
2
3

提示：

• 1 <= s.length <= 1000
• s 只包含小写英文字母，竖线 ‘|’ 和星号 ‘*’ 。
• s 包含 偶数 个竖线 ‘|’ 。

2. 思路分析

定级Easy。
按题意模拟即可。

3. 代码实现

class Solution:
    def countAsterisks(self, s: str) -> int:
        x = s.split('|')
        ans = 0
        for i in range(0,len(x),2):
            ans += x[i].count('*')
        return ans            
1
2
3
4
5
6
7

三、[Medium] 6106. 统计无向图中无法互相到达点对数

链接: 6106. 统计无向图中无法互相到达点对数

1. 题目描述

6106. 统计无向图中无法互相到达点对数

难度：中等

给你一个整数 n ，表示一张** 无向图** 中有 n 个节点，编号为 0 到 n - 1 。同时给你一个二维整数数组 edges ，其中 edges[i] = [ai, bi] 表示节点 ai 和 bi 之间有一条 无向 边。

请你返回 无法互相到达 的不同 点对数目 。

示例 1：

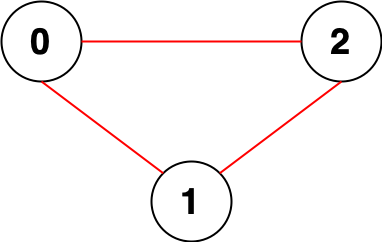
输入：n = 3, edges = [[0,1],[0,2],[1,2]]
输出：0
解释：所有点都能互相到达，意味着没有点对无法互相到达，所以我们返回 0 。

1
2
3
4

示例 2：

输入：n = 7, edges = [[0,2],[0,5],[2,4],[1,6],[5,4]]
输出：14
解释：总共有 14 个点对互相无法到达：
[[0,1],[0,3],[0,6],[1,2],[1,3],[1,4],[1,5],[2,3],[2,6],[3,4],[3,5],[3,6],[4,6],[5,6]]
所以我们返回 14 。

1
2
3
4
5
6

提示：

• 1 <= n <= 105
• 0 <= edges.length <= 2 * 105
• edges[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• 不会有重复边。

2. 思路分析

定级Medium。

• 并查集处理家族。
• 统计每个家族的数量，显然这个家族的人和别的家族的人都不能连通，相乘即可。
• 最后结果要除2，因为所有点对都计算了两遍。

3. 代码实现

class UnionFind:
    def __init__(self,size):
        self.fathers = list(range(size))
    def find_father(self,x):
        return self._zip_find_father(x)    
    def _zip_find_father(self,x):
        fathers = self.fathers
        if fathers[x] != x:
            fathers[x] = self._zip_find_father(fathers[x])
        return fathers[x]                      
    def union(self,x,y):
        x = self.find_father(x)
        y = self.find_father(y)
        if x == y:
            return False
        self.fathers[x] = y       
        return True 
    def is_same_father(self,x,y):
        return self.find_father(x)==self.find_father(y)
    
class Solution:
    def countPairs(self, n: int, edges: List[List[int]]) -> int:
        uf = UnionFind(n)
        
        for u,v in edges:
            uf.union(u,v)
            
        cnt = Counter()
        for i in range(n):
            cnt[uf.find_father(i)]+=1
        vs = list(cnt.values())
        # print(len(vs))
        ans = 0
        for i in range(len(vs)):            
            ans += vs[i]*(n-vs[i])
        return ans//2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

四、[Medium] 6105. 操作后的最大异或和

链接: 6105. 操作后的最大异或和

1. 题目描述

6105. 操作后的最大异或和

难度：中等

给你一个下标从 0 开始的整数数组 nums 。一次操作中，选择 任意 非负整数 x 和一个下标 i ，更新 nums[i] 为 nums[i] AND (nums[i] XOR x) 。

注意，AND 是逐位与运算，XOR 是逐位异或运算。

请你执行 任意次 更新操作，并返回 nums 中所有元素 最大 逐位异或和。

示例 1：

输入：nums = [3,2,4,6]
输出：7
解释：选择 x = 4 和 i = 3 进行操作，num[3] = 6 AND (6 XOR 4) = 6 AND 2 = 2 。
现在，nums = [3, 2, 4, 2] 且所有元素逐位异或得到 3 XOR 2 XOR 4 XOR 2 = 7 。
可知 7 是能得到的最大逐位异或和。
注意，其他操作可能也能得到逐位异或和 7 。
1
2
3
4
5
6

示例 2：

输入：nums = [1,2,3,9,2]
输出：11
解释：执行 0 次操作。
所有元素的逐位异或和为 1 XOR 2 XOR 3 XOR 9 XOR 2 = 11 。
可知 11 是能得到的最大逐位异或和。
1
2
3
4
5

提示：

• 1 <= nums.length <= 105
• 0 <= nums[i] <= 108

2. 思路分析

定级Medium。
不会做，看大佬解析：

• 每个操作实际上可以把每一位变成任意1或0。
• 那么我们最后答案中，这位有1就能保留；没1没办法
• 因此最后所有数字或即可，取每一位的1.

3. 代码实现

class Solution:
    def maximumXOR(self, nums: List[int]) -> int:
        ans = 0
        for n in nums:
            ans |= n
        return ans
1
2
3
4
5
6

五、[Hard] 6107. 不同骰子序列的数目

链接: 6107. 不同骰子序列的数目

1. 题目描述

6107. 不同骰子序列的数目

难度：困难

给你一个整数 n 。你需要掷一个 6 面的骰子 n 次。请你在满足以下要求的前提下，求出 不同 骰子序列的数目：

1. 序列中任意 相邻 数字的 最大公约数 为 1 。
2. 序列中 相等 的值之间，至少有 2 个其他值的数字。正式地，如果第 i 次掷骰子的值 等于 第 j 次的值，那么 abs(i - j) > 2 。

请你返回不同序列的 总数目 。由于答案可能很大，请你将答案对 109 + 7 取余 后返回。

如果两个序列中至少有一个元素不同，那么它们被视为不同的序列。

示例 1：

输入：n = 4
输出：184
解释：一些可行的序列为 (1, 2, 3, 4) ，(6, 1, 2, 3) ，(1, 2, 3, 1) 等等。
一些不可行的序列为 (1, 2, 1, 3) ，(1, 2, 3, 6) 。
(1, 2, 1, 3) 是不可行的，因为第一个和第三个骰子值相等且 abs(1 - 3) = 2 （下标从 1 开始表示）。
(1, 2, 3, 6) i是不可行的，因为 3 和 6 的最大公约数是 3 。
总共有 184 个不同的可行序列，所以我们返回 184 。
1
2
3
4
5
6
7

示例 2：

输入：n = 2
输出：22
解释：一些可行的序列为 (1, 2) ，(2, 1) ，(3, 2) 。
一些不可行的序列为 (3, 6) ，(2, 4) ，因为最大公约数不为 1 。
总共有 22 个不同的可行序列，所以我们返回 22 。

1
2
3
4
5
6

提示：

• 1 <= n <= 104

2. 思路分析

定级Hard。
dp。
比赛时试图只记录上一个数，用了dp[n][6]，失败了，状态转移没想明白。
后来写了下可以记两个数。

• 枚举第i个数时，这个数不能和前俩数相等，且和前一个数gcd必须是1，才能转移，
• 因此可以在这里剪枝搜索。
• 这里给出记忆化搜索代码。

3. 代码实现

class Solution:
    def distinctSequences(self, n: int) -> int:
        mod = 10**9+7
        @cache
        def dfs(i,last,last2):
            if i == 0:
                return 1
            ans = 0
            for j in range(1,7):
                if j != last and j != last2 and gcd(j,last) == 1:
                    ans += dfs(i-1,j,last)
                    ans %= mod
            return ans
        return dfs(n,7,7)
1
2
3
4
5
6
7
8
9
10
11
12
13
14

六、参考链接

• 链接: https://mp.csdn.net/mp_blog/creation/success/125129040