1.算法部分仿真预览

      软切换是WCDMA系统的关键技术之一，软切换算法和相关参数的设置直接影响着系统的容量和服务质量。通过WCDMA系统的软切换技术可以提高小区覆盖率和系统容量。所以软切换技术是WCDMA系统中一个十分关键的技术。首先，在概述WCDMA系统的无线资源管理功能和切换技术的基础上，详细介绍了WCDMA系统中的软切换过程。通过Matlab对WCDMA进行系统级的仿真，并对传统的软切换技术进行仿真分析，提出了其存在的缺陷，然后在此基础上提出了改进的软切换算法，并对改进后的算法进行了性能分析。通过研究，WCDMA软切换对下行容量的影响与软切换比例密切相关，在相同的条件下，改进后的软切换算法较传统的软切换算法，具有更佳的软切换增益值。本文总结得到的仿真结果，可以作为WCDMA系统实际应用的参考和借鉴。

       软切换，指的是用户的移动设备在载波频率相同的小区之间进行信道的切换。在软切换的过程中，用户完全有可能同时和两个或更多的基站进行通信，在切换过程中，软切换不需要改变设备的频率，也不会出现信号中断的情况，通常情况下，软切换进一步能分为软切换和更软切换两种类型。软切换：在这种切换过程中，当移动台开始与一个新的基站联系时，并不立即中断与原来基站之间的通信，即“先连后断”。

图1 软切换基本过程

      软切换过程和硬切换相似，就是在区域边界出会频繁的出现反复切换的现象，这也是所谓的乒乓效应。但由于软切换过程是先连后断进行，所以一般不会出现硬切换中频繁掉话的现象。而更软切换则是软切换的一种特殊情况。这种切换形式发生在同一基站的具有相同频率的不同扇区之间。软切换和更软切换的主要区别在于：软切换发生在两个Node-B之间，分集信号在RNC中合并处理；而更软切换则发生在同个Node-B内，分集信号在Node-B中做最大增益合并。这里，具体就不多做介绍了。

       通常，WCDMA系统中的软切换过程划分为以下三个步骤：无线测量、网络判决、系统执行。软切换执行的阶段示意图如下：

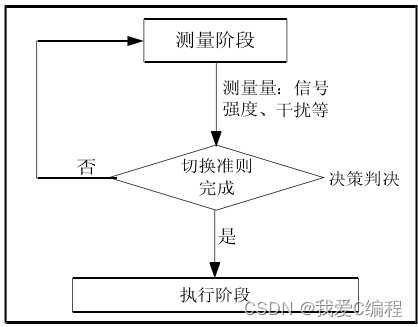
图2 WCDMA软切换执行流程

      其中，无线测量由UE和Node-B完成的；网络判决在RNC中进行；系统执行在UE、Node-B和RNC共同协作下完成。

      切换测量阶段，移动台要首先要测量下行链路的信号质量、所属的小区及临近小区的信号能量；测量结果被送到相关的RRC层。

      切换判决阶段。测量结果与预先设定的门限进行比较，以决定是否执行切换操作，同时要进行接纳控制，防止别的小区由于别的用户的加入，从而导致降低已有用户的通信质量。

       在执行阶段，移动台先进入软切换状态，RNC根据测量结果判决切换的目标，并通知移动台进行切换，一个新基站或小区被加入、释放或者替换。

 

clc;
clear;
close all;
warning off;
addpath(genpath(pwd));
% QQ   : 1480526168
% 微信 : lovemike121
% matlab/FPGA项目合作
 
%注意为了增加仿真速度，对不同指标的仿真，采用单独仿真的方法
% 1:仿真边缘覆盖率
% 2:************************
% 3:仿真改进算法的软切换增益
% 4：对比2，3.
% 5：小区覆盖范围
% 6：下行软切换增益
select = 5;
 
% 以上是旧算法中提取的数据，下面根据负载因数来计算新算法的参数取值
% 负载因素
index = 1;
for i = 0.1:0.01:0.6
f(index) = 1;
index = index + 1;
end
for i = 0.601:0.01:1
f(index) = 1.137-0.637*i^3;   
index = index + 1;
end
 
figure
plot(f,'r-*');
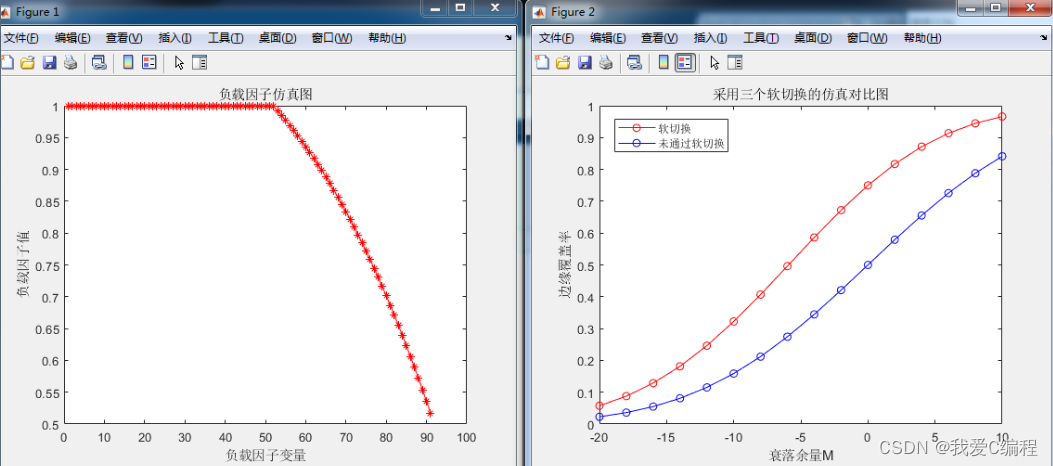
title('负载因子仿真图');
xlabel('负载因子变量');
ylabel('负载因子值');
 
 
 
 
index = 1;
for i = 0.1:0.001:0.6
f(index) = 1;
index = index + 1;
end
for i = 0.601:0.001:1
f(index) = 1.137-0.637*i^3;   
index = index + 1;
end
 
 
if select == 1
%将负载因子引入到参数选择中，
%边缘覆盖率算法对比
figure;
delta=10;
M    =0:1:40;
Y = 0.5 + 0.5*erf(M/(sqrt(2)*delta));
plot(Y,'b-o');title('边缘覆盖率与衰落余量');hold on;
 
delta= 10;
M    = 0:1:40;
pp   = 0.773;
k    = 1;
Y = 0.5 + 0.5*erf(M/(k*f(1000*pp)*sqrt(2)*delta));
plot(Y,'r-o');title('边缘覆盖率与衰落余量');
legend('传统算法','改进算法');
grid on;
 
xlabel('衰落余量M');
ylabel('边缘覆盖率');
end
 
 
 
 
if select == 2
%软切换增益
figure;
delta = 10;
a     = 0.7071;
b     = 0.7071;
M     = -20:2:10;
index = 1;
n     = 3;
for i = 1:length(M)
syms  x;    
i
v=0;
Q=0;
data3 = 0;
v=((M(i)+a*delta*x)/(b*delta));
Q = 1/(sqrt(2*pi))*int(exp(-x^2/2),x,v,100);
data3 = 1 - 1/(sqrt(2*pi))*int(exp(-x^2/2)*Q^n,x,-100,100);
value2(i) = double(data3);
index = index + 1;
end
 
plot(M,value2,'r-o');hold on
Y = 0.5 + 0.5*erf(M/(sqrt(2)*delta));
plot(M,Y,'b-o');title('采用三个软切换的仿真对比图');hold off
legend('软切换','未通过软切换');
save value2.mat value2
 
xlabel('衰落余量M');
ylabel('边缘覆盖率');
end
 
 
if select == 3
%软切换增益
figure;
delta = 10;
a     = 0.7071;
b     = 0.7071;
M     = -20:2:10;
pp    = 0.773;
k     = 1;
index = 1;
n = 3;
for i = 1:length(M)
syms  x;    
i
v=0;
Q=0;
data3 = 0;
v=((M(i)+a*delta*x)/(b*delta/(k*f(1000*pp))));
Q = 1/(sqrt(2*pi))*int(exp(-x^2/2),x,v,100);
data3 = 1 - 1/(sqrt(2*pi))*int(exp(-x^2/2)*Q^n,x,-100,100);
value3(i) = double(data3);
index = index + 1;
end
 
plot(M,value3,'r-o');hold on
Y = 0.5 + 0.5*erf(M/(sqrt(2)*delta));
plot(M,Y,'b-o');title('采用三个软切换的仿真对比图');hold off
legend('软切换','未通过软切换');
save value3.mat value3
xlabel('衰落余量M');
ylabel('边缘覆盖率');
end
 
if select ==4
    M = -20:2:10;
    load value2.mat
    load value3.mat
    
    plot(M,value2,'r-o');hold on
    plot(M,value3,'b-o');hold off
    legend('原算法','改进后算法');    
    xlabel('衰落余量M');
    ylabel('软切换增益');
end
 
if select == 5
    figure;
    load value2.mat
    load value3.mat    
    M=8:0.25:9;
    for i = 1:length(M)
    Ss_Sh1(i)=10^(M(i)/(40)); 
    Ss_Sh2(i)=10^((1+(value3(i)-value2(i)))*M(i)/(40)); 
    end
    plot(10*M,Ss_Sh2,'b-o');hold on;
    plot(10*M,Ss_Sh1,'r-o');hold on;
   
    
    legend('改进后的算法的小区面积扩大倍数','传统算法的小区面积扩大倍数');
    title('小区面积扩大倍数的分析仿真图');
    xlabel('边界覆盖率');
    ylabel('小区面积扩大倍数');    
end
 
 
 
 
 
if select == 6
    
   pp    = 0.603;
   k     = 1; 
    
   figure;
   Rh_R=0:0.1:0.9;
   for i=1:length(Rh_R)
      x(i) = (1 - 2*pi/(3*sqrt(3))*Rh_R(i)^2); 
   end
   subplot(121);
   plot(Rh_R,x,'r-*');title('软切换开销（比例）');
   xlabel('边界覆盖范围');
   ylabel('软切换开销'); 
   %由于计算公式是否复杂，以下数据是传统的方法得到的，根据数据计算得到改进后的数据
   XX   = [0   5    10   15    20   25   30   35    40    45  ];
   Ps1A = [10  12.5 12.8 10    7.75 9.25 7.25 12    16.25 9.75];
   Ps1S = [0.5 1.0  0.63 0.44  0.3  0.41 0.4  0.68  0.77  0.97];
   PSHO = [0.6 0.2  0.5  0.43  0.4  0.5  0.4  0.88  1.77  0.97];
   
   G=(Ps1A./(Ps1S + PSHO)) -1 ;
   subplot(122);
   plot(XX,G,'b-*');title('下行软切换增益');grid on;hold on;
   G=(Ps1A./(Ps1S + (k*f(1000*pp))*PSHO)) -1 ;
   plot(XX,G,'r-o');title('软切换增益');grid on;   
   legend('传统算法','改进后算法');
    xlabel('衰落余量M');
    ylabel('下行软切换增益');
end
 
 
 
 

 

 

 

2.源码获取方式

获得方式1：

点击下载链接：

m基于matlab的wcdma软切换算法的研究分析和仿真+word版lun文 +程序操作视频

获取方式2：

博客资源项，搜索和博文同名资源。

获取方式3：

如果下载链接失效，加博主微信联系。