系列文章目录

刷题笔记（一）–数组类型：二分法
刷题笔记（二）–数组类型：双指针法
刷题笔记（三）–数组类型：滑动窗口
刷题笔记（四）–数组类型：模拟
刷题笔记（五）–链表类型：基础题目以及操作
刷题笔记（六）–哈希表：基础题目和思想
刷题笔记（七）–字符串：经典题目
刷题笔记（八）–双指针：两数之和以及延伸
刷题笔记（九）–字符串：KMP算法
刷题笔记（十）–栈和队列：基础题目
刷题笔记（十一）–栈和队列：Top-K问题
刷题笔记（十二）–复习：排序算法
刷题笔记（十三）–二叉树：前中后序遍历（复习）
刷题笔记（十四）–二叉树：层序遍历和DFS,BFS
刷题笔记（十五）–二叉树：属性相关题目
刷题笔记（十六）–二叉树：修改与构造
刷题笔记（十七）–二叉搜索树：关于属性问题
刷题笔记（十八）–二叉树：公共祖先问题
Leetcode 刷题笔记(十九) ——回溯算法篇之组合问题

前言

1.关于回溯算法

什么是回溯算法呢？其实之前我们在二叉树部分练习了大量的题目，对递归的使用贯穿了整个系列，但是这其中也包含了回溯的思想。回溯是递归的副产品，有了递归，就会有回溯。
所以所谓的回溯函数其实也就是递归函数。

2.回溯算法的效率

其实回溯算法的效率不高，因为回溯算法的总思想就是列举所有的子集然后去筛选，也就是穷举一遍之后，选出我们想要的答案。
如果想要效率高一点，也可以加一些剪枝的操作。但是也改变不了它穷举的本质，也改变不了它效率低的现实。那么既然效率不高，那为啥要使用呢？因为对于有些题目你只能这样做了，其他办法不行。比如：

3.可以解决的问题

回溯算法可以用来解决一下问题

组合问题：N个数里面按一定规则找出k个数的集合
切割问题：一个字符串按一定规则有几种切割方式
子集问题：一个N个数的集合里有多少符合条件的子集
排列问题：N个数按一定规则全排列，有几种排列方式
棋盘问题：N皇后，解数独等等
1
2
3
4
5

这些问题你可以发现基本都是坑，没有什么特别好的办法去解决，只有穷举一遍然后去筛选。
在这里再提一下组合和排列的区别

组合：无序的，比如[1,2],[2,1]就是相同的组合
排列：有序的，比如[1,2],[2,1]就是不同的排列

4.如何理解回溯算法

其实我们的回溯算法所解决的问题，都可以抽象为一个树形结构。因为回溯算法解决的都是在集合中递归查找子集，所以集合的大小就构成了树的宽度，递归的深度，构成树的深度。

因为递归肯定要有终止条件嘛，我们的回溯算法也是也一样的，所以这必然是一棵高度有限的树，后面的题我都会画图来解释。来，看题。

（PS：如果说在看题目的时候有点难理解或者对我做题的步骤有什么疑问，可以直接跳到最后，也就是解题模板部分。）

题录

77. 组合

题目链接如下：

77. 组合

题目截图如下：

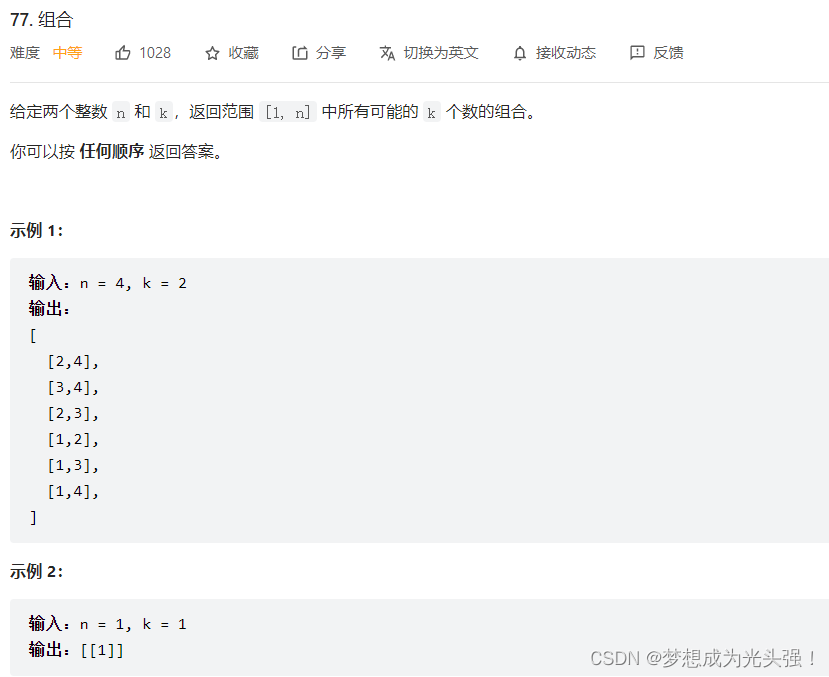
先分析一下，如果单纯从这一道题目来讲，我们第一个想法是什么呢？双层for循环是不是？

public List<List<Integer>> combine(int n, int k) {
        List<List<Integer>> list = new ArrayList<>();
        for (int i = 1; i <= n; i++) {
            for (int j = i + 1; j <= n; j++) {
                list.add(Arrays.asList(i,j));
            }
        }
    }
1
2
3
4
5
6
7
8

但是哈，但是，如果n = 80，k = 25呢？来一个25层循环？估计谁来谁都要疯。所以这里就可以让我们的回溯算法上场了。

可以用回溯算法把这个for循环拆开，拆成25层递归的形式，然后每一层都有一个for循环。图示如下：

这里我们就可以发现，n就是宽度，k就是深度。没当我们要收集结果的时候，就遍历其中一条路，最后直到叶子结点就可以了。

1.确定方法和参数以及返回值

首先就是要知道我们用什么来收集

List<List<Integer>> list = new ArrayList<>();//结果集
List<Integer> mylist = new ArrayList<>();//收集当前遍历的节点
1
2

然后这里我们需要三个参数

树的宽度，树的深度，以及下一层递归搜索的起始位置

public void backtracking(int n,int k,int index){

    }
1
2
3

2.明确终止条件

啥时候停止呢？就是遍历到了根节点，也就是当前链表的长度等于k的时候就可以把当前链表加入到结果集当中。

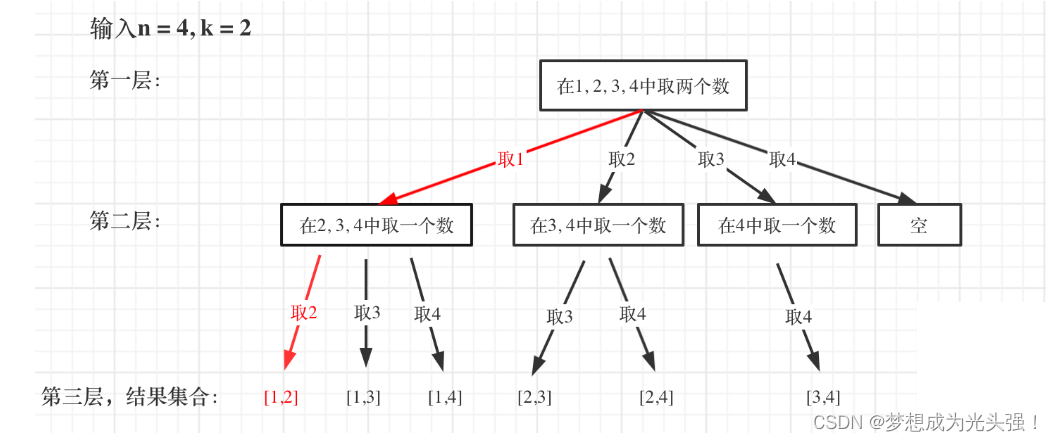
对应代码如下：

public void backtracking(int n,int k,int index){
        //终止条件
        if(mylist.size() == k) {
            list.add(mylist);
            return;
        }
    }
1
2
3
4
5
6
7

3.等价关系式

这里就是明确每一层递归干的事情了。把当前节点的值加入当前集合，然后完了之后进行记得撤销本次处理的结果，并且去遍历同一层次的其他节点。

for(int i = index;i < n;i++){
            mylist.add(i);//添加当前节点
            backtracking(n,k,index+1);//进行同一层次的其他节点的遍历
            mylist.removeLast();//撤销本次操作
        }
1
2
3
4
5

所以最后的代码如下：

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;

public class 组合 {
    List<List<Integer>> list = new ArrayList<>();//结果集
    LinkedList<Integer> mylist = new LinkedList<>();//收集当前遍历的节点
    public List<List<Integer>> combine(int n, int k) {
        backtracking(n,k,1);
        return list;
    }

    public void backtracking(int n,int k,int index){
        //终止条件
        if(mylist.size() == k) {
            list.add(new ArrayList<>(mylist));
            return;
        }
        for(int i = index;i <= n;i++){
            mylist.add(i);//添加当前节点
            backtracking(n,k,i+1);//进行同一层次的其他节点的遍历
            mylist.removeLast();//撤销本次操作
        }
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

4.关于优化问题

这里的话其实我们可以对等价关系式进行优化

for(int i = index;i <= n;i++){
       mylist.add(i);//添加当前节点
       backtracking(n,k,i+1);//进行同一层次的其他节点的遍历
       mylist.removeLast();//撤销本次操作
}
1
2
3
4
5

但是这里其实有一个小小的问题，就是如果比如说n = 4,k = 4的时候，就会有很多没有意义的遍历

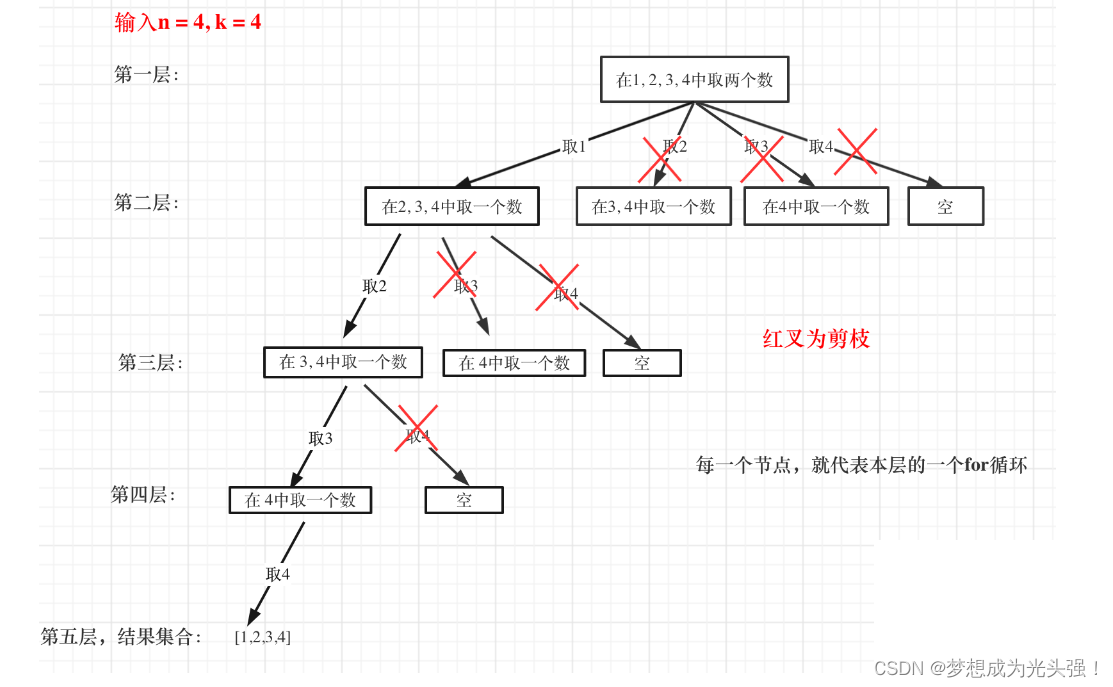
因为你可以发现如果说后序的元素个数不满足我们需要的个数就没有必要再继续递归下去了。所以，可以剪枝的地方就在递归中每一层的for循环所选择的起始位置。

这里

mylist.size()：就是我们已经确定了的元素个数
k - mylist.size()：就是我们需要的元素个数

所以下面的遍历就可以从n - (k - mylist.size()) + 1开始遍历，为什么是+1呢？因为我们的遍历是包含起始位置的，所以优化之后的整体代码如下：

public class 组合 {
    List<List<Integer>> list = new ArrayList<>();//结果集
    LinkedList<Integer> mylist = new LinkedList<>();//收集当前遍历的节点
    public List<List<Integer>> combine(int n, int k) {
        backtracking(n,k,0);
        return list;
    }

    public void backtracking(int n,int k,int index){
        //终止条件
        if(mylist.size() == k) {
            list.add(mylist);
            return;
        }
        for(int i = index;i < n - (k - mylist.size()) + 1;i++){
            mylist.add(i);//添加当前节点
            backtracking(n,k,i+1);//进行同一层次的其他节点的遍历
            mylist.removeLast();//撤销本次操作
        }
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

216. 组合总和 III

题目链接如下：

216. 组合总和 III

题目截图如下：

老规矩，三步走起

1.确定方法和参数

public class 组合总和3 {
    List<List<Integer>> list = new ArrayList<>();
    LinkedList<Integer> mylist = new LinkedList<>();
    public List<List<Integer>> combinationSum3(int k, int n) {
    
    }

    public void backtracting(int n,int k,int sum,int index){
        
    }
}

1
2
3
4
5
6
7
8
9
10
11
12

这里我需要四个参数

n：目标数字总和
k：目标数字长度
sum：当前数字总和
startIndex：遍历数字的起始位置

2.明确终止条件

啥时候终止呢？就是总和为目标数并且长度也刚刚好的时候

if(sum == n && mylist.size() == k){
            //如果说当前数字的总和等于n并且长度是k，就返回
            list.add(new ArrayList<>(mylist));
            return;
        }
1
2
3
4
5

3.等价关系式

接下来就是细分每一层递归

for(int i = startIndex;i < 10;i++){
            mylist.add(i);
            backtracting(n,k,sum+i,i+1);
            mylist.removeLast();
        }
1
2
3
4
5

所以最后的总代码如下：

public class 组合总和3 {
    List<List<Integer>> list = new ArrayList<>();
    LinkedList<Integer> mylist = new LinkedList<>();
    public List<List<Integer>> combinationSum3(int k, int n) {
        backtracting(n,k,0,1);
        return list;
    }

    public void backtracting(int n,int k,int sum,int startIndex){
        if(sum == n && mylist.size() == k){
            //如果说当前数字的总和等于n并且长度是k，就返回
            list.add(new ArrayList<>(mylist));
            return;
        }
        for(int i = startIndex;i < 10;i++){
            mylist.add(i);
            backtracting(n,k,sum+i,i+1);
            mylist.removeLast();
        }
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

4.关于优化问题

这个也是可以优化的哈，因为其中也是有很多没有必要的遍历条件。这里的话优化可以从两点下手

1.当前总和如果说大于目标值，直接返回
2.当前mylist长度大于目标值，直接返回

代码的话有两种书写方式

public class 组合总和3 {
    List<List<Integer>> list = new ArrayList<>();
    LinkedList<Integer> mylist = new LinkedList<>();
    public List<List<Integer>> combinationSum3(int k, int n) {
        backtracting(n,k,0,1);
        return list;
    }

    public void backtracting(int n,int k,int sum,int startIndex){
        if(sum == n && mylist.size() == k){
            //如果说当前数字的总和等于n并且长度是k，就返回
            list.add(new ArrayList<>(mylist));
            return;
        }
        //在这里进行剪枝
        if(sum > n || mylist.size() > k) return;
        for(int i = startIndex;i < 10;i++){
            mylist.add(i);
            backtracting(n,k,sum+i,i+1);
            mylist.removeLast();
        }
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

第二种应该才算是剪枝吧，这种的话就不用再多进行一层递归了

public class 组合总和3 {
    List<List<Integer>> list = new ArrayList<>();
    LinkedList<Integer> mylist = new LinkedList<>();
    public List<List<Integer>> combinationSum3(int k, int n) {
        backtracting(n,k,0,1);
        return list;
    }

    public void backtracting(int n,int k,int sum,int startIndex){
        if(sum == n && mylist.size() == k){
            //如果说当前数字的总和等于n并且长度是k，就返回
            list.add(new ArrayList<>(mylist));
            return;
        }
        //在这里进行剪枝
        //if(sum > n || mylist.size() > k) return;

		//第二种：对于 mylist.size() > k在for循环遍历条件进行限制
        for(int i = startIndex;i <= 9 - (k-mylist.size()) + 1;i++){
            mylist.add(i);
            if(sum + i <= n) {
                backtracting(n, k, sum + i, i + 1);
            }
            mylist.removeLast();
        }
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

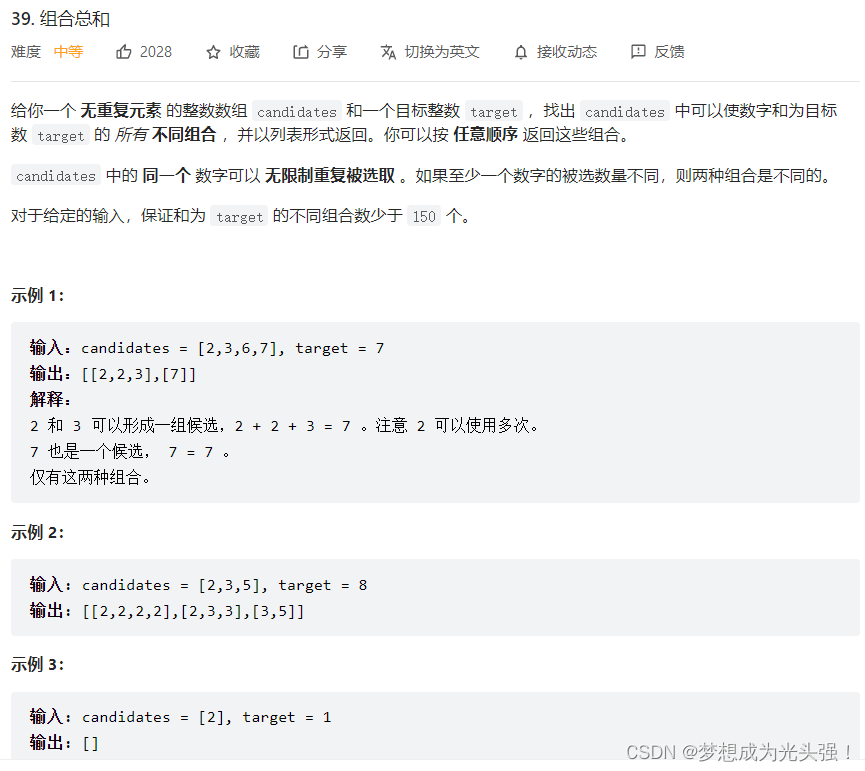
39. 组合总和

题目链接：

39. 组合总和

题目截图：

这个题目和上面的题目一模一样，但是有一个地方的处理需要特别注意，笔者刚开始练习的时候总是犯一个错误，看下面的图

笔者在这里犯的错误就是这个下标，然后发现了新大陆
<1>如果写的是i：如果说你当前写的不是i + 1而是i，那么你就会得到一组包含重复值的集合的目标值。什么意思呢？拿当前题目举个例子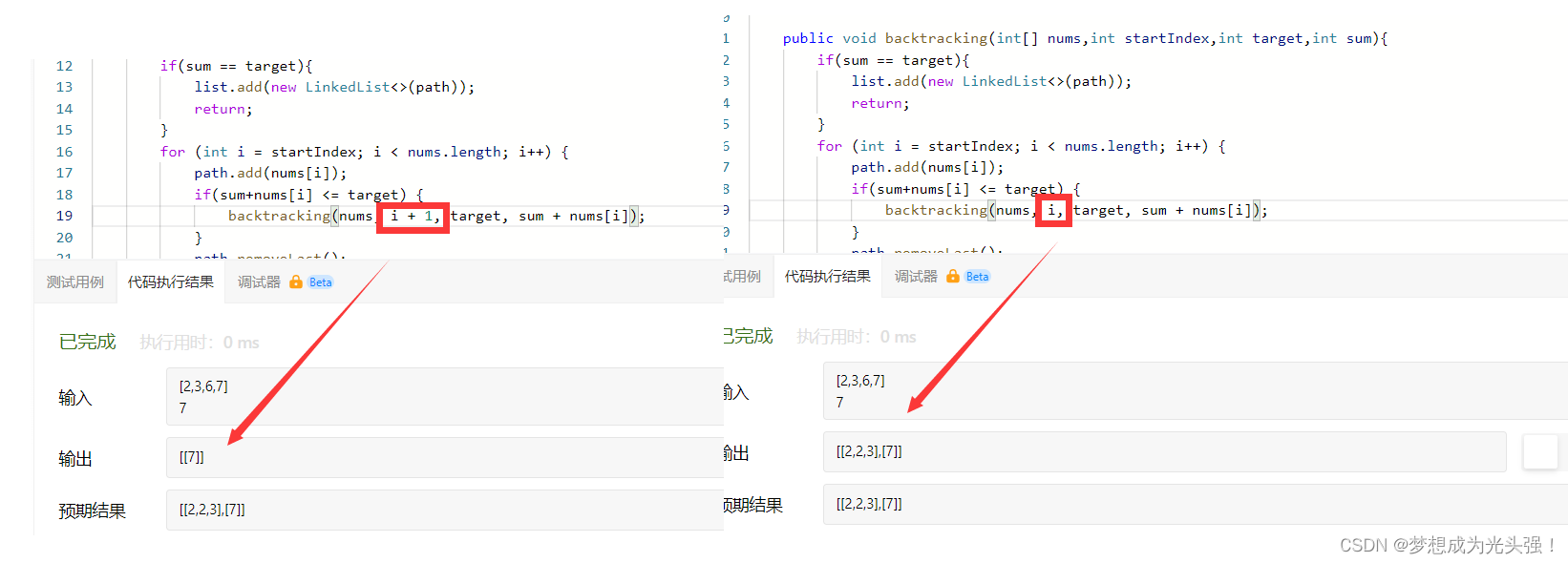

<2>如果你写的是startIndex而不是i：那么你就会得到一组排列顺序不同并且总和等于目标值的集合

好了，扯远了，开始这道题目的讲解，下面就直接贴代码了，因为思想和上面的题目一模一样。

1.确定方法和参数

public class 组合总和 {

    List<List<Integer>> list = new ArrayList<>();//最终的元素集合
    LinkedList<Integer> path = new LinkedList<>();

    public List<List<Integer>> combinationSum(int[] candidates, int target) {
       
    }

    public void backtracking(int[] nums,int startIndex,int target,int sum){
        
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14

2.明确终止条件

public class 组合总和 {

    List<List<Integer>> list = new ArrayList<>();//最终的元素集合
    LinkedList<Integer> path = new LinkedList<>();

    public List<List<Integer>> combinationSum(int[] candidates, int target) {
       
    }

    public void backtracking(int[] nums,int startIndex,int target,int sum){
        if(sum == target){
            list.add(new LinkedList<>(path));
        }
        
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

3.等价关系式

public class 组合总和 {

    List<List<Integer>> list = new ArrayList<>();//最终的元素集合
    LinkedList<Integer> path = new LinkedList<>();

    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        backtracking(candidates,0,target,0);
        return list;
    }

    public void backtracking(int[] nums,int startIndex,int target,int sum){
        if(sum == target){
            list.add(new LinkedList<>(path));
        }
        for (int i = startIndex; i < nums.length; i++) {
            path.add(nums[i]);
            backtracking(nums, i, target, sum + nums[i]);
            path.removeLast();
        }
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

4.关于优化问题

优化问题还是和上面一样，但是有一点不同，就是它对于长度没有要求，所以就不能在for的判断条件下手了，所以这里能剪枝的

public void backtracking(int[] nums,int startIndex,int target,int sum){
        if(sum == target){
            list.add(new LinkedList<>(path));
        }
        for (int i = startIndex; i < nums.length; i++) {
            path.add(nums[i]);
            if(sum+nums[i] <= target) {
                backtracking(nums, i, target, sum + nums[i]);
            }
            path.removeLast();
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12

其实笔者在做题的时候还看到了其他答案，是在

这里增加了一个排序，为什么会增加这个排序呢？

//增加排序的意义也是为了剪枝，剪枝的位置和咋们的位置差不多
for (int i = startIndex; i < nums.length; i++) {
            if(sum + nums[i] > target) break;
            path.add(nums[i]);
            backtracking(nums, i, target, sum + nums[i]);
            path.removeLast();
        }
//因为这里如果是有序数组，那么当前值的和已经大于target了，后续就没有必要再进行读取。
//当前这里先排序再剪枝的效率是比我直接剪枝的效率高的
1
2
3
4
5
6
7
8
9

40. 组合总和 II

题目链接如下：

40. 组合总和 II

题目截图如下：

这道题目和上面就有点区别啦，对于等价关系式就需要好好琢磨琢磨了。

1.确定方法和参数

public class 组合总和2 {
    List<List<Integer>> list = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
    }

    public void backstcking(int[] candidates,int startIndex,int target,int sum){
        
    }
}
1
2
3
4
5
6
7
8
9
10

2.明确终止条件

public class 组合总和2 {
    List<List<Integer>> list = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
    
    }

    public void backstcking(int[] candidates,int startIndex,int target,int sum){
        if(sum == target){
            list.add(new ArrayList(path));
            return;
        }
        
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

3.等价关系式

在这里，就要好好的说一说了，因为这就是这道题的重点和难点所在。在来看一遍题目

每一个数字在每个组合当中只能使用一次，这就是这道题的限制条件也就是让原先的题目上升了一个档次的所在。
可能很多同学不知道这个是什么意思，这里所谓的在每个组合当中只能使用一次是个啥东西？没关系，看下面这个图

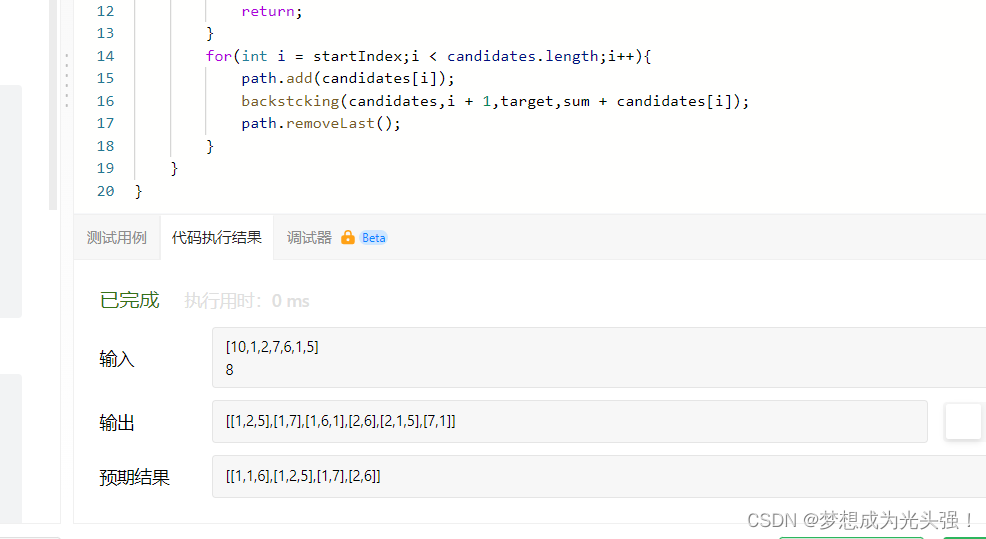
这样输出的话，是不是就能直观很多？说白了其实就是不能有相同的集合。但是集合里面的元素可以相同。
还没明白？没关系，那就先跟着我的思路往下走。上面我们说过了，任何一个回溯问题（递归）都可以转化成一个树模型，这里的关键点就在于你是否对树模型有了真正的认识。树模型的深度和宽度就是代表了两个不同的层次，而题目中的“使用过”，我们从不同的层次来思考就有不同的结果。这里我们应该从什么方面来思考呢？没错，树的宽度

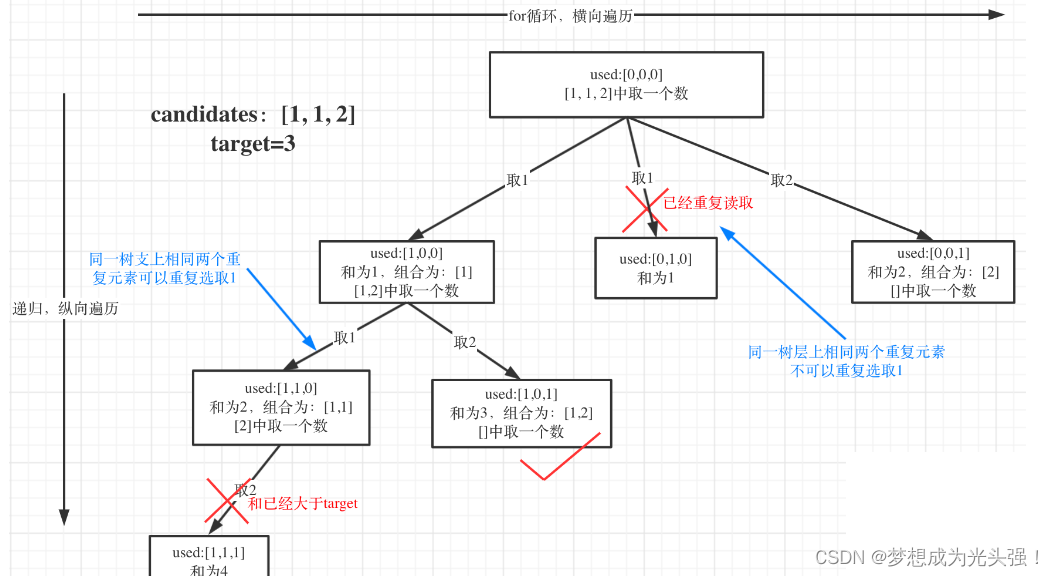
所以其实你这样想的话就很简单了，直接让数组排序为非递减数组，然后如果说nums[i - 1] ==nums[i]，就证明当前元素已经被排序过了，那么就不用考虑此元素集合。

代码如下：

public class 组合总和2 {
    List<List<Integer>> list = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
    	Arrays.sort(candidates);
        backstcking(candidates,0,target,0);
        return list;
    }

    public void backstcking(int[] candidates,int startIndex,int target,int sum){
        if(sum == target){
            list.add(new ArrayList(path));
            return;
        }
        for(int i = startIndex;i < candidates.length;i++){
            if ( i > startIndex && candidates[i] == candidates[i - 1] ) {
                continue;
            }
            path.add(candidates[i]);
            backstcking(candidates,i + 1,target,sum + candidates[i]);
            path.removeLast();
        }
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

编译会通过

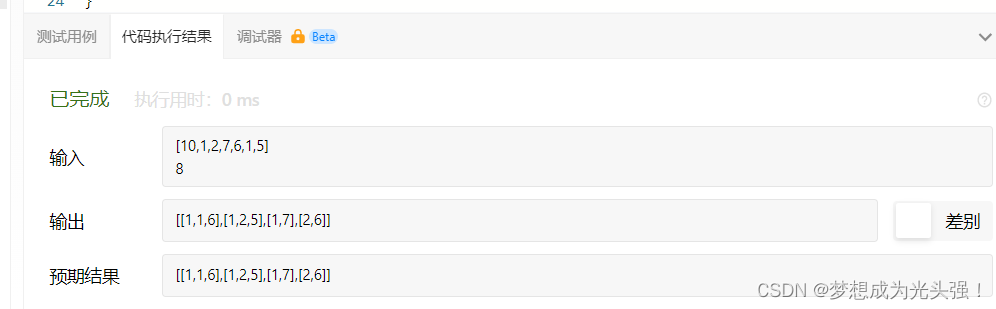
但是你提交就过不了了，运行时间过长了

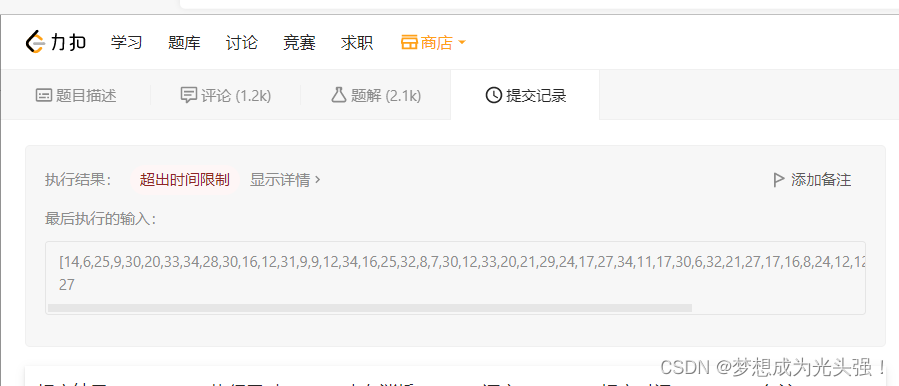
这个时候我们第四步的重要性就凸显出来了

4.关于优化问题

这里的话就是进行剪枝，也就是直接加一个判断语句

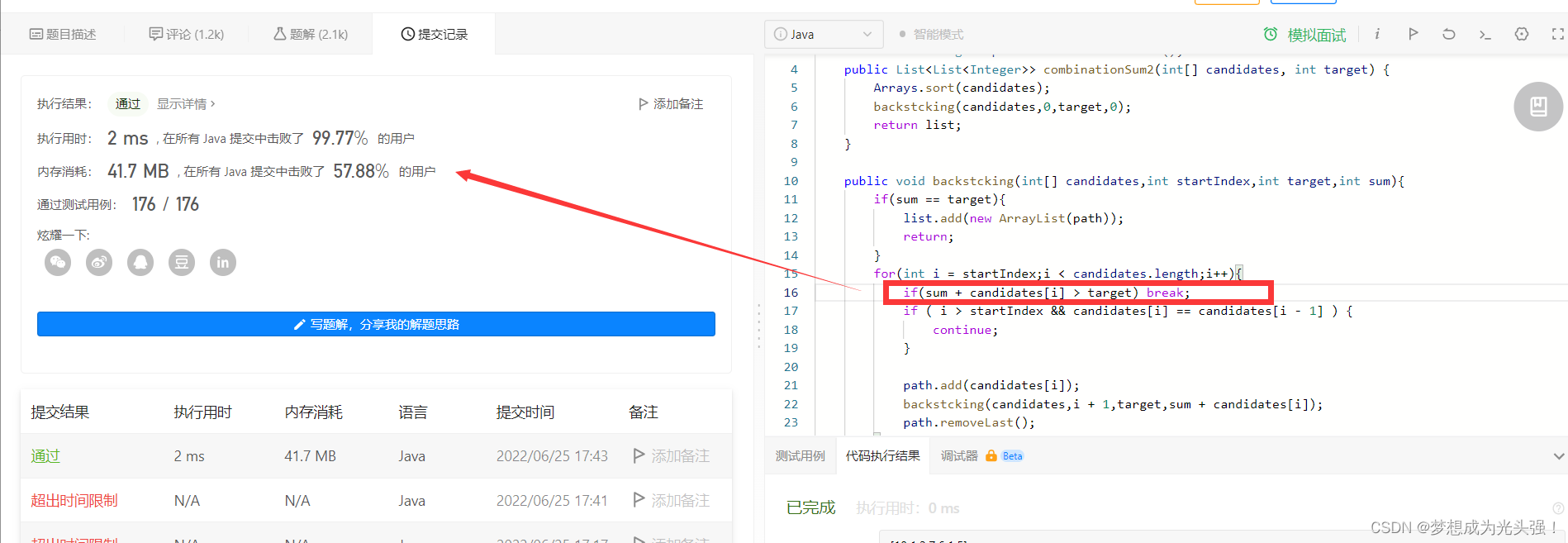
当然你觉得影响代码的美观性你也可以把这行代码加入for循环的判断语句

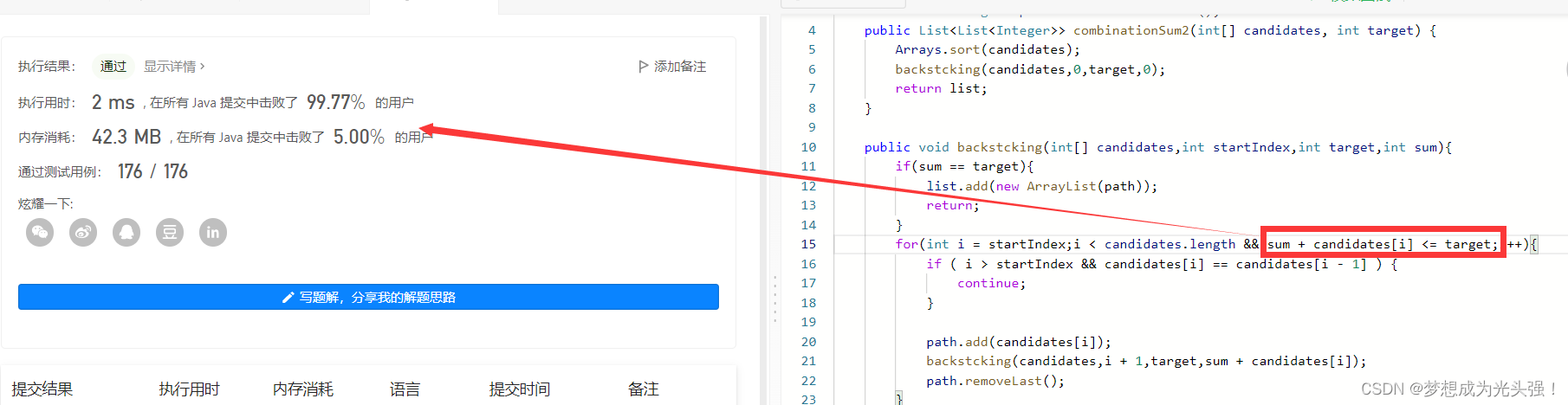
17. 电话号码的字母组合

题目链接如下：

17. 电话号码的字母组合

题目截图如下：

这一道题目和上面的题目没什么太大区别，看图示

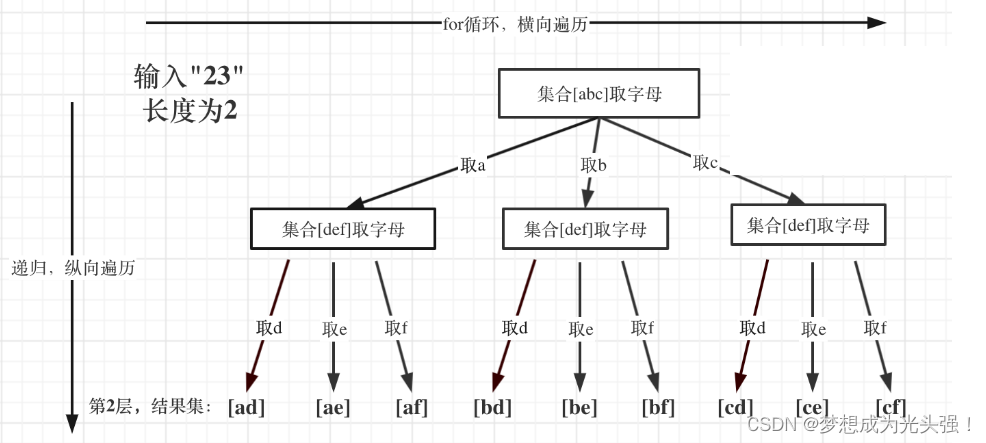
难点就是在数字和字母的映射，还有就是不同字符串中取值的变化。

这里就不全面分析了，直接给代码

public class 电话号码的字母组合 {

    List<String> list = new LinkedList<>();//用来存储结果集
    public List<String> letterCombinations(String digits) {
        if(digits.length() == 0 || digits == null) return list;
        String[] numString = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
        backstacking(digits,numString,0);
        return list;
    }

    StringBuilder str = new StringBuilder();//构建一个字符串构造器，用来做对应的删减工作

    public void backstacking(String digits,String[] numString,int num){
        if(num == digits.length()){
            list.add(str.toString());
            return;
        }

        String myStr = numString[digits.charAt(num) - '0'];
        for (int i = 0; i < myStr.length(); i++) {
            str.append(myStr.charAt(i));
            backstacking(digits,numString,num+1);
            str.deleteCharAt(str.length() - 1);
        }
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

解题模板

这一部分是关于回溯的解题模板的。

$1.确定方法和参数$

public void backtracking(参数)
1

注意，这里的参数要根据实际题目给出。然后既然是回溯（递归），那么刚开始就是要确定终止条件。

如果有对递归问题的解决步骤不熟悉的小伙伴可以看我这里的这篇博客
JavaSE – 方法（下）–浅谈递归

$2.明确终止条件$

那么终止条件也就是我们递归的结束条件，也就是到了叶子结点。到了这里就可以把这个答案存起来来了，并且当前递归结束。

if (终止条件) {
    存放结果;
    return;
}
1
2
3
4

$3.等价关系式$

这一步就是最重要的，也就是把每一层递归拆开处理，明确你的处理方式。当然，在回溯算法这里，我们是在通过递归得出来一个集合，然后在集合中搜索，所以集合的大小就是树的宽度，递归的深度就是树的高。

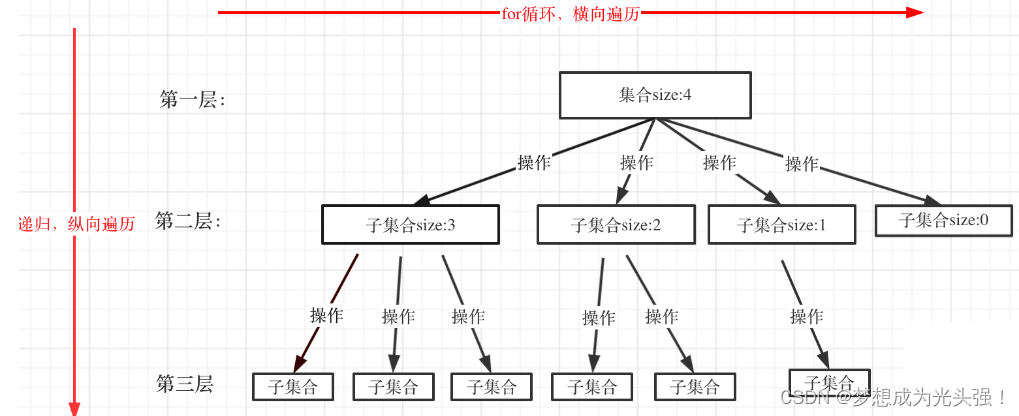
所以集合的多少和孩子数量相等。所以代码如下：

for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
    处理节点;
    backtracking(路径，选择列表); // 递归
    回溯，撤销处理结果
}
1
2
3
4
5

这里的for循环就是遍历集合区间，可以理解为一个节点有多少个孩子，这个for循环就执行多少次，至于递归调用这，就是根据你自己的情况进行选择。
这样理解吧，for循环可以理解是横向遍历，backtracking（递归）就是纵向遍历，这样就把这棵树全遍历完了，一般来说，搜索叶子节点就是找的其中一个结果了。

所以最后总结代码模板如下：

public void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}
1
2
3
4
5
6
7
8
9
10
11
12