基于差分进化与优胜劣汰策略的灰狼优化算法

摘要：为了改善灰狼优化算法收敛速度慢、寻优精度低、易早熟等缺陷，提出一种改进的灰狼优化算法。在基本灰狼优化算法的基础上，引入差分进化机制生成 1 个变异种群，通过其动态缩放因子和交叉概率因子避免算法陷入局部最优。引入优胜劣汰的生物竞争淘汰策略，根据比较进化变异后狼群个体适应度值淘汰 m 只狼，同时随机生成与被淘汰狼数量相同的狼。

1.灰狼优化算法

基础灰狼算法的具体原理参考，我的博客：https://blog.csdn.net/u011835903/article/details/107716390

2. 改进灰狼优化算法（IGWO）

2.1 GWO 算法中的差分进化

自然界中生物在其生存环境影响下，通过遗传、选择和变异不断地从低级向高级进化和发展 。这种物竞天择、适者生存的进化机制将使灰狼种群变得越来越强大，受此思想影响，将差分进化思想融入 GWO 算法中，避免基本 GWO 算法陷入局部极值，提高 GWO 算法整体搜索能力。

狼群根据环境朝着好的方向进化是保证种群竞争力的基础，而理想的矢量变异因子是保证GWO 算法向最优解方向搜索进化的基础，为此选择竞争力较强的优秀灰狼个体( 优秀解位置) 作为进化种群的父代，经过实验测试确定 β 和 δ2 只狼的差分矢量，经过动态缩放因子与 α 狼叠加，以构建出基于差分进化的 GWO 算法的变异因子，其变异因子矢量函数表达式为：
$${\mathbf{V}}_i^{t+1}={\mathbf{X}}_{\alpha }^t+W\cdot \left({\mathbf{X}}_{\beta }^t-{\mathbf{X}}_{\delta }^t\right)\text{\hspace{1em}(17)}$$
式中: W 为动态变化的缩放因子，其取值方式如下:
$$W=\left(f_{\max }-f_{\min }\right)\cdot \frac{t_{\max }-(t-1)}{t_{\max }}+f_{\min }\text{\hspace{1em}(18)}$$
式中: $f_{min}$ 和$f_{max}$ 为缩放因子的最小值和最大值，tmax为最大迭代次数，t 为当前迭代次数。动态变化的缩放因子 W 针对基本 GWO 算法在搜索前期易陷入局部极值的缺陷，通过增大缩放因子动态调整差分矢量，提高 GWO 算法在搜索前期的全局探索能力，通过减小缩放因子使 GWO 算法在搜索后期具有较强的局部开发能力，提高其搜索精度。

将狼群中的目标个体 $X_i^t$ 与所得的变异矢量$V_i^{t+1}$进行交叉操作产生中间个体 $U_i^{t+1}$。通过随机选择的方式使 $U_i^{t+1}$中至少有 1 位基因是由 $V_i^{t+1}$提供的，才能保证$X_i^t$发生变异。对于其他的基因影响情况，通过交叉概率因子$S$与产生的随机数进行比较，以此来确定变异基因是由 $V_{t+1}^i$提供的还是由$X_i^t$ 提供的。其交叉操作为
U i t + 1 = { X i j S < rand ⁡ ( j )  and  j ≠ rand ⁡ ( i ) V i j t + 1 S ⩾ rand ⁡ ( j )  or  j = rand ⁡ ( i ) (19) \boldsymbol{U}_{i}^{t+1}=\left\{

\right. \tag{19} Uit+1​={Xij​Vijt+1​​S<rand(j) and j​=rand(i)S⩾rand(j) or j=rand(i)​(19)
式中: $S$ 表示交叉概率常数，通过适当地选取交叉概率 S，不但可以提高收敛速度和增强局部搜索能力，还可以加快全局搜索速度和提高解的多样性; 利用随机维数变量 rand( i) 保证狼群个体矢量最少有 1 维变量来自变异矢量 V t ij ，以确保经过进化所产生的新个体相异于父代个体矢量 ;rand( j) 为在［0，1］内服从均匀分布的随机数。

狼群中灰狼个体将通过竞争产生新一代个体。经过变异和交叉操作产生中间个体$U_i^{t+1}$，与个体 $X_i^t$ 竞争，选择适应度值好的个体作为下一代狼群个体.
X i t + 1 = { X i t f ( X i t ) ⩽ f ( V i t + 1 ) V i t + 1 f ( X i t ) > f ( V i t + 1 ) (20) \boldsymbol{X}_{i}^{t+1}=\left\{

\right. \tag{20} Xit+1​={Xit​Vit+1​​f(Xit​)⩽f(Vit+1​)f(Xit​)>f(Vit+1​)​(20)
式中: $f$ 为构造的适应度函数，狼群中个体之间的距离小于 $f_{close}$ ，其取值为：
$$f_{\text{close }}=\frac{1}{2^k}\sqrt{\sum _{i=0}^k{\left(f_{i,\max }-f_{i,\min }\right)}^2}\text{\hspace{1em}(21)}$$
式中: $k$ 为目标函数数量，$f_{i,max}$ 和 $f_{i，min}$ 为第$i$ 个目标函数的最大值和最小值，选择 $X_i^t$ 和 $V_i^{t+1}$中适应度值好的作为第$t+1$代个体。

2.2 狼群算法中的优胜劣汰策略

在自然界中，狼群中存在 1 种动态平衡，即被淘汰狼与新加入狼之间的平衡，以此增强整个狼群的竞争能力，保证狼群在复杂的环境中生存 。受此启发，利用 1 种优胜劣汰策略更新灰种群。
灰狼种群经过差分变异后形成一定数量的新一代狼群个体，狼群优胜劣汰策略使那些在搜索猎物过程中陷入局部最优和处于狼群较低级别的灰狼个体不再参与搜索，提前退出自己的生命周期，在狼群更新阶段，被淘汰的灰狼个体亦不再参与。优胜劣汰策略以灰狼个体的适应度值大小衡量灰狼个体的强弱，适应度值越小灰狼个体的优越性越强。因此，在狼群每一代差分变异后对新一代灰狼个体按适应度值进行升序排列，淘汰适应度值较大的 m 只狼，并随机生成与被淘汰灰狼相同数量的灰狼以保持狼群的稳定。被淘汰灰狼数量 m 对狼群的更新有重要影响，m 越大狼群个体的多样性越强，即 GWO 算法解的多样性就强。但如果 m 过大，算法中新生解的个数增多，算法的随机性增强，将导致算法收敛速度变慢; 如果 m 过小，算法中新生解的个数减少，算法的多样性降低，开发能力减弱，易陷入局部最优。因此，为了保证算法在探索与开发之间维持好平衡设定.
$$m=[n/\eta ,n/(0.618\cdot \eta )]\text{\hspace{1em}(22)}$$
式中: n 为灰狼个体数量，η 为更新比例因子，m取值范围上下限满足黄金分割比例。

算法流程图如下：

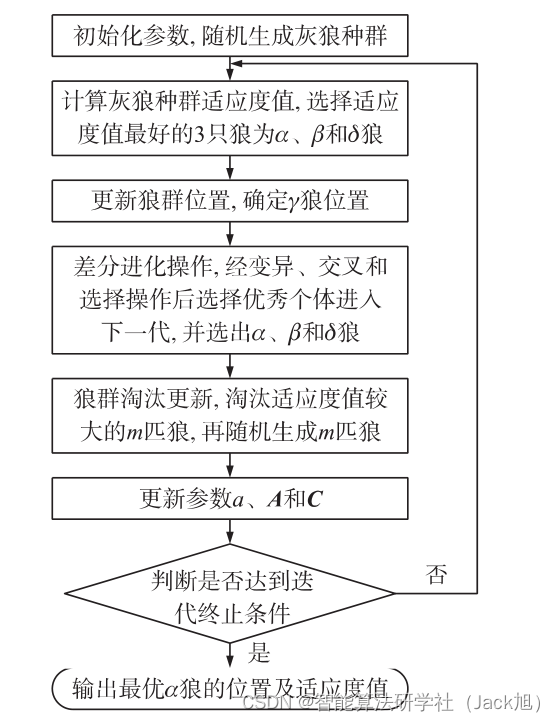
3.实验结果

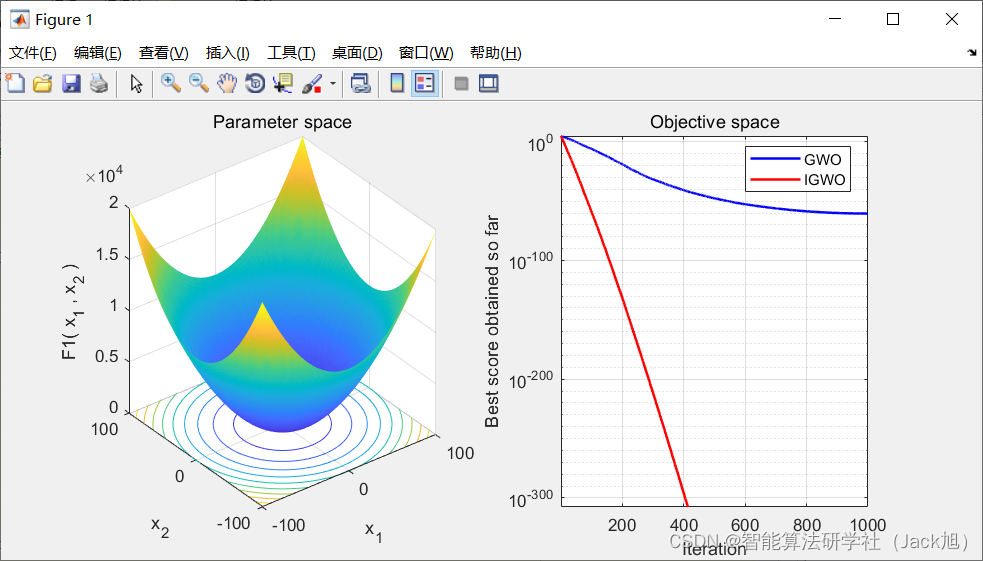
4.参考文献

[1]朱海波,张勇.基于差分进化与优胜劣汰策略的灰狼优化算法[J].南京理工大学学报,2018,42(06):678-686.

5.Matlab代码

6.Python代码