• 【堆排序】十大排序算法之堆排序

    【堆排序】十大排序算法之堆排序，是【不稳定】的排序算法。

    目录

    一、什么是堆

    1.1、二叉树

    1.2、满二叉树

    1.3、完全二叉树

    1.4、堆

    二、堆排序基本思想

    三、堆排序代码实现

    3.1、无序序列构建成大顶堆

    3.2、重新调整为大顶堆

    3.3、堆排序代码实现

    （1）堆排序代码

    （2）堆排序代码优化

    一、什么是堆

    堆，是一种数据结构，它是一个完全二叉树的数据结构。

    1.1、二叉树

    什么是完全二叉树？？？要了解完全二叉树，就需要知道什么是二叉树？？？

    二叉树：树中每个结点最多只有两个子结点，满足这种特点的树，叫做：二叉树。

    二叉树案例：

    1.2、满二叉树

    满二叉树，所谓的满二叉树就是指：

    树中除了叶子结点之外，其余每个结点的度都是【2】，那么符和这种结构的二叉树就叫做：满二叉树。

    一颗具有【n】个结点的满二叉树，具有如下特点：

    • 满二叉树不存在度为【1】的结点，只存在度为【0】和【2】的结点，并且度为【0】的都是叶子结点。
    • 满二叉树，第【i】层上，具有【2^(i-1)】个结点。
    • 深度为【k】的满二叉树，总共具有【2^k - 1】个结点，最后一层具有【2^(k - 1)】个结点。
    • 具有【n】的结点的满二叉树，其深度为【log2(n + 1)】。

    满二叉树案例：

    1.3、完全二叉树

    完全二叉树，除了最后一层结点，其余每层结点都是满二叉树，并且最后一层结点是从左往右依次展示的。

    完全二叉树，首先它必须是一颗二叉树，然后这颗二叉树满足如下特点：

    • 一颗深度为【h】的有【n】个结点的二叉树，树中每个结点，从左往右，从上往下，依次进行编号。
    • 如果编号为【i】的结点，与满二叉树中编号为【i】的结点位置相同，那么这种二叉树就叫做：完全二叉树。

    完全二叉树，可以看作是除了最后一层之外，其余结点都是满二叉树的树。

    完全二叉树具有如下特点：

    • 完全二叉树的叶子结点，只能出现在最下层、次下层。
    • 一颗具有【n】个结点的完全二叉树，它的深度是：【log2(n) + 1】。
    • 如果对一颗具有【n】个结点的完全二叉树，从左往右，从上往下进行编号，那么任意结点【i】具有如下特点：
      • 如果【i = 1】，则该节点是根节点；
      • 如果【i > 1】，则该结点的父节点是：【i / 2】。
      • 如果【2*i > n】，则结点【i】没有左孩子，否则其左孩子是【2*i】。
      • 如果【2*i + 1 > n】，则结点【i】没有右孩子，否则其右孩子是【2*i + 1】。

    完全二叉树案例：

    1.4、堆

    堆就是利用了完全二叉树的这个数据结构，然后规定：完全二叉树中的每个结点，必须小于（或大于）等于其左右孩子结点。

    堆又分为两种结构：小根堆（小顶堆）、大根堆（大顶堆）。

    • 小根堆：完全二叉树中的每个结点，都【小于或等于】其【左右孩子节点】。
    • 大根堆：完全二叉树中的每个结点，都【大于或等于】其【左右孩子节点】。

    注意：堆中左右孩子结点没有大小要求，只要保证左右孩子结点和根节点的大小关系即可。

    小根堆案例：

    大根堆案例：

    如果我们按照层序遍历的方式，将堆中每个结点采用数组保存起来，那么小根堆、大根堆保存结果如下所示：

    采用数组这种结构，刚好可以利用完全二叉树的特点，即：某个结点【i】，可以通过【2*i】和【2*i + 1】找到其对应的左右孩子结点。

    但是，数组是从下标【0】开始的，所以我们需要转换一下，某个结点【i】，其左右结点位置：

    • 左结点位置是：【2*i + 1】；
    • 右结点位置是：【2*i + 2】；

    对于小根堆数组，其每个元素满足：

    • arr[i] <= arr[2*i + 1] && arr[i] <= arr[2*i + 2]；
    • 前提是下标不越界。

    对于大根堆数组，其每个元素满足：

    • arr[i] >= arr[2*i + 1] && arr[i] >= arr[2*i + 2]；
    • 前提是下标不越界。

    知道堆着这种数据结构之后，我们可以来学习堆排序来了。

    二、堆排序基本思想

    • 堆排序，是【选择类】的排序算法。
    • 堆排序，是【不稳定】的。
    • 堆排序，时间复杂度：【O(n*log(n))】。
    • 堆排序，空间复杂度：【O(1)】。

    什么是稳定的排序？？？

    稳定排序：

    • 如果排序数组中，存在相同的元素，假设存在两个元素【3】。
    • 为了标识两个元素【3】的先后顺序，我们假设给她命名为：【3(1)】、【3(2)】。
    • 其中括号里面的表示元素3出现的先后顺序。
    • 如果结果排序之后，两个元素还是保持相同的顺序，即：【3(1)、3(2)】，那么我们就称这个排序是稳定的，否则就是不稳定的排序。

    堆排序基本思想（大根堆）

    这里以【大根堆】为案例，介绍一下堆排序的基本思想，采用【大根堆】是升序排序。

    基本思想：

    1. 假设有一个无序的待排序数组【arr】。
    2. 排序开始之前，需要将待排序数组【arr】构建成一个【大根堆】数组【heap】。
    3. 此时，大根堆数组【heap】中第【0】个元素就是最大值。
    4. 将【大根堆】数组【heap】中第【0】个元素和【heap】中最后一个元素交换位置，此时最大值就位于数组最后一个位置。
    5. 第一次堆排序完成，但是这个时候，数组【arr】前【n-1】个元素就不满足堆的结构，所以我们需要将前【n-1】个元素重新调整为【大根堆】结构。
    6. 重新调整前【n-1】个结点为【大根堆】。
    7. 重复2、3、4、5、6步骤，直到第【1】个元素结束。
    8. 此时，堆排序完成。

    核心步骤：

    • 构建大顶堆。
    • 交换【根元素】和最后一个叶子结点。
    • 重新构建大顶堆。

    堆排序大致思路如下图所示：

    • 构建初始堆结构【大顶堆】。

    •  交换【大顶堆】根节点和其最后一个叶子结点。

    •  交换【6】和【13】之后，除去【13】结点，其余结点就不再是堆的结构了，所以需要重新调整堆结构。

    • 将二叉树重新调整为大顶堆后， 交换【大顶堆】根节点和其倒数第二个叶子结点。

    • 上面交换之后，除了【12】、【13】结点之外，其余的结点又不满足堆的结构，所以需要重新调整为大顶堆结构。
    • 依次类推，直到最后交换到根结点时候，此时整个堆如下所示。

    • 可以看到，上面最终形成的堆，变成了一个小顶堆，并且按照层次遍历是有序的（从小到大排序的）。
    • 层次遍历序列：【4、5、6、7、8、9、11、12、13】，排序完成。

    到这里，堆排序的过程演示结束。可以从这个网站查看堆排序的过程【数据结构和算法动态可视化 (Chinese) - VisuAlgo】。

    三、堆排序代码实现

    堆排序的大致过程我们知道了，但是如何通过代码来实现呢？？？

    因为我们是知道怎么把一个待排序数组构建成大顶堆，并且在排序过程中可以很清楚知道，如何重新调整为大顶堆，但是对于计算机来说，它是不知道的，那怎么办呢？？？？

    我们可以采用数组来保存数据，然后通过下标就可以方便的找到某个结点对应的左右孩子结点。

    堆排序需要解决下面两个问题：

    1. 如何将一个无序的序列构建成一个大顶堆结构。
    2. 如何重新调整为一个大顶堆结构。

    3.1、无序序列构建成大顶堆

    下面采用这个【5, 11, 4, 13, 7, 9, 8, 12, 6】无序序列为案例，介绍如何将其初始化为一个大顶堆结构。

    • 初始无序序列数组。

    • 先将初始的无序序列看层一个完全二叉树结构，如下图所示。

    • 下面，就需要将初始的完全二叉树构建成一个堆结构。
    • 最开始，我们从最后一个结点开始，找到第一个存在【左右结点】的结点。
    • 如果存在【左右结点】，就比较【当前结点】和其【左右结点】的大小，找到三个结点中最大的结点，然后将【最大值结点】和【当前结点i】交换位置。
    • 如果【当前结点】就是最大值结点，那就可以不要交换，直接继续判断前一个结点。
    • 从【6】开始往前查找，发现第一个具有【左右子结点】的是【13】结点。
    • 将【13】作为根节点，与其【左右子结点】调整为一个【大顶堆】结构，发现【13】就是最大值，所以不用调整。

    • 继续找前一个结点，前一个结点是【4】，具有【左右子结点】。
    • 将【4】作为根节点，与其【左右子结点】比较，发现【9】是最大值，于是将【4】和【9】交换位置，形成一个【大顶堆】结构。

    • 继续找前一个结点，前一个结点是【11】，具有【左右子结点】。
    • 将【11】作为根节点，与其【左右子结点】比较，发现【13】是最大值，于是将【11】和【13】交换位置，形成一个【大顶堆】结构。

    • 上面将【11】为根节点的调整为大顶堆结构后，会出现一个问题，就是以【11】为根节点的二叉树又不满足堆的结构了，因为【11、12、6】三个数字里面，【12】应该作为根节点，所以我们需要重新调整一下以【11】为根结点的二叉树结构。

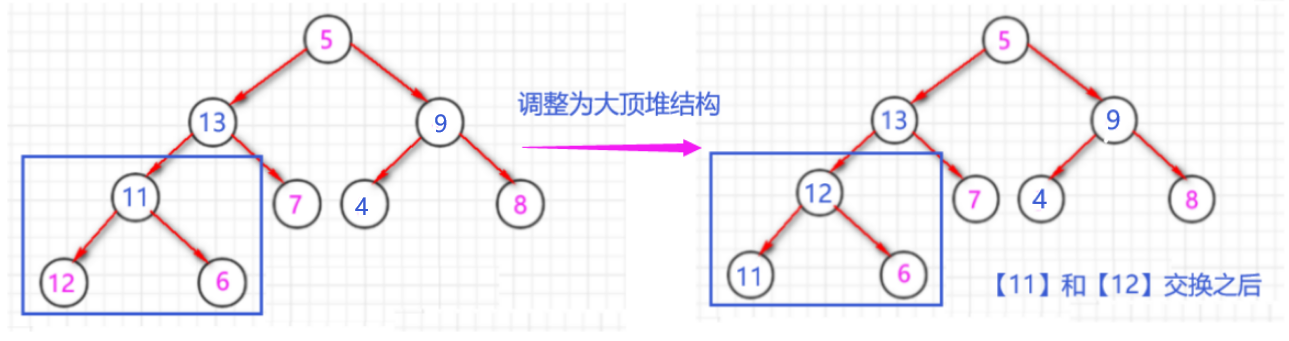
    • 从上面【13】和【11】两个结点调整过程中，可以看出，当我们在调整某个结点为大顶堆的过程里面，调整之后，可能会将之前已经调整好的大顶堆结构给破坏了，为了解决这个问题，所以就还需要将以调整之后的那个结点为根节点的二叉树，再次进行调整。
    • 例如：【11】和【13】交换之后，虽然以【13】为根节点的二叉树是【大顶堆】结构了，但是为了确保以【11】为根节点的二叉树也满足堆的结构，所以还需要将以【11】为根节点的二叉树再次进行调整。
    • 上面这种情况，就可以采用【递归】的方式来实现。
    • 当我们某一次进行了【大顶堆】调整时，说明有交换元素，那么我们这个时候，就递归的将被交换的元素结点为根节点，再次进行【大顶堆】调整，递归的结束条件是：【当没有交换元素时候结束递归，也即：已经是大顶堆结构了】。
    • 继续找前一个结点，前一个结点是【5】，具有【左右子结点】。
    • 将【5】作为根节点，与其【左右子结点】比较，发现【13】是最大值，于是将【5】和【13】交换位置，形成一个【大顶堆】结构。

    • 【13】和【5】调整之后，发现以【5】为根节点的二叉树又不满足堆的结构了，所以又要重新调整以【5】为根节点的二叉树，利用递归的思路，继续调整。

    •  【12】和【5】调整之后，发现以【5】为根节点的二叉树又不满足堆的结构了，所以又要重新调整以【5】为根节点的二叉树，利用递归的思路，继续调整。

    •  到此时，整个无序序列就已经构建成了一个【大顶堆】结构，如下所示。

    思考一个问题？？？

    • 我们每次在调整一个结点为大顶堆的时候，递归取调整它下一层结点的时候，为什么可以确保它上一层结点仍然保持大顶堆结构？？？
    • 例如：
      • 前面我们调整【13】和【5】两个结点的时候，交换【13】和【5】两个结点，之后【13】是大顶堆结构，但是【5】不是，我们就需要去调整【5】为大顶堆，那为什么【5】调整为大顶堆结构后，不会影响到【13】为根节点的大顶堆结构呢？？？

     思考问题的答案：

    • 为什么下层调整为大顶堆结构不会影响上一层的大顶堆结构呢？？？？
    • 原因是：
      • 我们是从最后一个结点开始调整，那么每次调整的时候，都会将最大值移到上一层，所以对于某个结点来说，以他为根节点的二叉树，他一定是整个二叉树的最大值，无论你下一层结点怎么调整，都必定是小于或者等于根节点，所以就不会影响到上一层的大顶堆结构。
      • 也就是说：每次调整都是将最大值调整到上一层，类似于冒泡，每次将最大值冒泡出来。

    3.2、重新调整为大顶堆

    当我们构建好初始化的大顶堆结构后，利用堆排序的思想，将堆中根节点和其最后一个结点交换位置，此时最大值位于最后一个结点，那么前【n-1】个结点就可能不满足堆结构，就需要重新调整前【n-1】个结点为堆结构。

    • 【根节点】和【最后一个结点】交换位置。

    • 进行一次堆排序之后，发现除了【13】结点之外，其余结点又不是堆结构，所以需要重新调整为堆结构。
    • 那这不是就是相等于将前【n-1】个无序序列构建为大顶堆的过程吗？？？和【3.1】步骤是一样的做法。
    • 这里就不再画图了。
    • 一直进行堆排序，最终形成的堆结构如下所示。

    【大顶堆】采用堆排序后，最终形成的堆结构，不就是【小顶堆】结构吗，并且是一个层次遍历按照升序排列的【小顶堆】。

    3.3、堆排序代码实现

    （1）堆排序代码

    1. import java.util.Arrays;
    2.  
    3. /**
    4.  * @version 1.0.0
    5.  * @Date: 2022/6/19 11:45
    6.  * @Author ZhuYouBin
    7.  * @Description
    8.  */
    9. public class HeapSort {
    10.     /** 堆排序: O(n * log(n)) */
    11.     public static void heapSort(int[] nums) {
    12.         int len = nums.length;
    13.         // 1、无序序列构建为大顶堆
    14.         buildHeap(nums, len);
    15.         System.out.println("构建初始大顶堆: " + Arrays.toString(nums));
    16.         // 2、交换【大顶堆】中【根节点】和【最后结点】位置
    17.         for (int i = len - 1; i >= 0; i--) {
    18.             // 交换【0】和【i】结点位置
    19.             swap(nums, 0, i);
    20.             // 重新将前【len - 1】个结点调整为大顶堆
    21.             len--;
    22.             // 调整【0】根节点大顶堆结构
    23.             heapify(nums, 0, len);
    24.         }
    25.     }
    26.     /**
    27.      * 构建堆结构
    28.      * @param nums 无序序列
    29.      * @param len 结点个数，即数组元素个数
    30.      */
    31.     public static void buildHeap(int[] nums, int len) {
    32.         // 从最后一个结点开始调整【大顶堆】结构
    33.         for (int i = len - 1; i >= 0; i--) {
    34.             // 调整结点【i】为大顶堆结构
    35.             heapify(nums, i, len);
    36.         }
    37.     }
    38.     /**
    39.      * 调整堆结构方法
    40.      * @param nums 满足堆结构的数组
    41.      * @param i 当前需要调整的结点
    42.      * @param len 当前堆结构长度
    43.      */
    44.     public static void heapify(int[] nums, int i, int len) {
    45.         // 获取当前结点【i】的左右孩子结点, 这里就是利用完全二叉树的特点
    46.         int left = 2 * i + 1; // 左孩子结点
    47.         int right = 2 * i + 2; // 右孩子结点
    48.         // 假设当前结点就是最大值
    49.         int largeIndex = i;
    50.         // 判断最大值在哪个位置
    51.         if (left < len && nums[left] > nums[largeIndex]) {
    52.             // 左结点是最大值
    53.             largeIndex = left;
    54.         }
    55.         if (right < len && nums[right] > nums[largeIndex]) {
    56.             // 右结点是最大值
    57.             largeIndex = right;
    58.         }
    59.         // 如果当前结点就是最大值,那就不用交换
    60.         if (largeIndex != i) {
    61.             // 交换当前结点【i】和【largeIndex】结点位置
    62.             swap(nums, i, largeIndex);
    63.             // 递归调整【largeIndex】为结点的二叉树
    64.             heapify(nums, largeIndex, len);
    65.         }
    66.     }
    67.     /** 交换元素位置 */
    68.     public static void swap(int[] nums, int i, int j) {
    69.         int temp = nums[i];
    70.         nums[i] = nums[j];
    71.         nums[j] = temp;
    72.     }
    73.  
    74.     public static void main(String[] args) {
    75.         int[] nums = {5, 11, 4, 13, 7, 9, 8, 12, 6};
    76.         System.out.println("原始的无序序列: " + Arrays.toString(nums));
    77.         heapSort(nums);
    78.         System.out.println("升序排序的序列: " + Arrays.toString(nums));
    79.     }
    80. }

    堆排序运行结果如下所示：

    （2）堆排序代码优化

    从前面代码里面，我们看到，我们构建初始化【大顶堆】的时候，是直接从最后一个结点开始往前判断，当遇见第一个具有【左节点】或者具有【右结点】的结点，此时就需要进行调整【大顶堆】操作，这样显然有一些循环是不必需要的。

    例如：叶子结点一定是没有孩子节点的，所以会执行很多次的空循环操作，我们可不可以避免这些空循环操作呢？？？

    避免空循环操作？？？

    开始调整【大顶堆】是从后往前，第一个遇见具有孩子结点的结点开始，根据完全二叉树的特点，它的第一个非叶子节点是第【n / 2】个结点。

    所以，我们就可以直接从第【n / 2】个结点往前开始调整【大顶堆】结构。

    但是由于数组是从【0】开始编号的，所以我们需要从【n / 2 - 1】位置开始往前调整【大顶堆】结构。

     优化后的代码如下所示:

    1. import java.util.Arrays;
    2.  
    3. /**
    4.  * @version 1.0.0
    5.  * @Date: 2022/6/19 11:45
    6.  * @Author ZhuYouBin
    7.  * @Description
    8.  */
    9. public class HeapSort {
    10.     /** 堆排序: O(n * log(n)) */
    11.     public static void heapSort(int[] nums) {
    12.         int len = nums.length;
    13.         // 1、无序序列构建为大顶堆
    14.         buildHeap(nums, len);
    15.         System.out.println("构建初始大顶堆: " + Arrays.toString(nums));
    16.         // 2、交换【大顶堆】中【根节点】和【最后结点】位置
    17.         for (int i = len - 1; i >= 0; i--) {
    18.             // 交换【0】和【i】结点位置
    19.             swap(nums, 0, i);
    20.             // 重新将前【len - 1】个结点调整为大顶堆
    21.             len--;
    22.             // 调整【0】根节点大顶堆结构
    23.             heapify(nums, 0, len);
    24.         }
    25.     }
    26.     /**
    27.      * 构建堆结构
    28.      * @param nums 无序序列
    29.      * @param len 结点个数，即数组元素个数
    30.      */
    31.     public static void buildHeap(int[] nums, int len) {
    32.         // 从最后一个结点开始调整【大顶堆】结构
    33.         for (int i = len / 2 - 1; i >= 0; i--) {
    34.             // 调整结点【i】为大顶堆结构
    35.             heapify(nums, i, len);
    36.         }
    37.     }
    38.     /**
    39.      * 调整堆结构方法
    40.      * @param nums 满足堆结构的数组
    41.      * @param i 当前需要调整的结点
    42.      * @param len 当前堆结构长度
    43.      */
    44.     public static void heapify(int[] nums, int i, int len) {
    45.         // 获取当前结点【i】的左右孩子结点, 这里就是利用完全二叉树的特点
    46.         int left = 2 * i + 1; // 左孩子结点
    47.         int right = 2 * i + 2; // 右孩子结点
    48.         // 假设当前结点就是最大值
    49.         int largeIndex = i;
    50.         // 判断最大值在哪个位置
    51.         if (left < len && nums[left] > nums[largeIndex]) {
    52.             // 左结点是最大值
    53.             largeIndex = left;
    54.         }
    55.         if (right < len && nums[right] > nums[largeIndex]) {
    56.             // 右结点是最大值
    57.             largeIndex = right;
    58.         }
    59.         // 如果当前结点就是最大值,那就不用交换
    60.         if (largeIndex != i) {
    61.             // 交换当前结点【i】和【largeIndex】结点位置
    62.             swap(nums, i, largeIndex);
    63.             // 递归调整【largeIndex】为结点的二叉树
    64.             heapify(nums, largeIndex, len);
    65.         }
    66.     }
    67.     /** 交换元素位置 */
    68.     public static void swap(int[] nums, int i, int j) {
    69.         int temp = nums[i];
    70.         nums[i] = nums[j];
    71.         nums[j] = temp;
    72.     }
    73.  
    74.     public static void main(String[] args) {
    75.         int[] nums = {5, 11, 4, 13, 7, 9, 8, 12, 6};
    76.         System.out.println("原始的无序序列: " + Arrays.toString(nums));
    77.         heapSort(nums);
    78.         System.out.println("升序排序的序列: " + Arrays.toString(nums));
    79.     }
    80. }

    这篇文章写的我好难受呀，好多图要画，期间还画错了，又得重新画图，有没有啥好的画图软件推荐的，我用的是processOn，FastStone。

    综上，这篇文章结束，主要介绍【堆排序】十大排序算法之堆排序，是【不稳定】的排序算法。

  • 相关阅读:
    【 Python高级编程】 Canny边缘检测算法阈值设置
    Webpack
    在Golang中依赖注入-wire篇
    【DDR3 控制器设计】（5）DDR3 的仲裁读写操作设计
    领悟《信号与系统》之 傅立叶变换的性质与应用
    2023.11.14 信息学日志
    ChineseChess5 2023.10.28
    kotlin(十七)Kotlin和Java相互调用
    关于webpack(v5.74.0)的html-webpack-plugin原理
    FFmpeg中的常用结构体分析
  • 原文地址：https://blog.csdn.net/qq_39826207/article/details/125354223