lt.62. 不同路径

[案例需求]

[思路分析一, 抽象为树进行DFS]

[代码实现]

1

[思路分析二, 动态规划]

• 机器人从(0,0)位置出发, 到达(m-1, n-1)中点;
• 按照动规五部曲来看:

1. 确定dp数组及其下标的含义:

dp[i][j]: 表示从(0, 0) 出发, 到(i,j)有dp[i][j]条不同的路径

2. 确定递推公式

想要求dp[i][j], 只能由两个方向推导出来(即向下和向右), 即dp[i - 1][j] 和 dp[i][j - 1];
回顾一下 dp[i - 1][j] 表示啥，是从(0, 0)的位置到(i - 1, j)有几条路径，dp[i][j - 1]同理。

3. dp数组的初始化

如何初始化呢，首先dp[i][0]一定都是1，因为从(0, 0)的位置到(i, 0)的路径只有一条，那么dp[0][j]也同理。 注意是路径奥, 可不是步数
所以初始化代码为：

for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;
1
2

4. 确定遍历顺序

这里要看一下递归公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1]，dp[i][j]都是从其上方和左方推导而来，那么从左到右一层一层遍历就可以了。
这样就可以保证推导dp[i][j]的时候，dp[i - 1][j] 和 dp[i][j - 1]一定是有数值的。

5. 举例推导dp数组
   

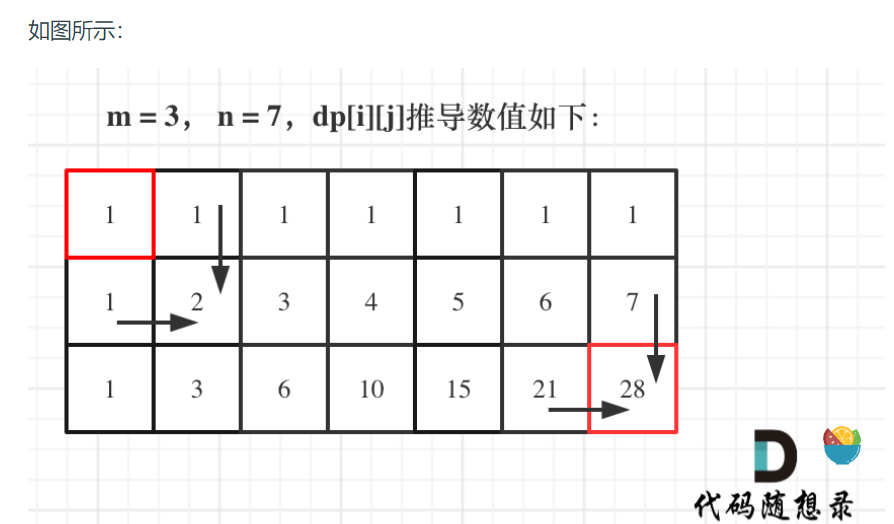
[代码实现]

class Solution {
    public int uniquePaths(int m, int n) {
        //1. dp数组: 走到(i,j)处需要多少步
        int[][] dp = new int[m][n];
        //2. 递推公式
        //dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
        //3. dp数组如何初始化
        for(int i = 0; i < m; i++){dp[i][0] = 1;}
        for(int j = 0; j < n; j++){dp[0][j] = 1;}
        //4. 确定遍历顺序
        //从左往右一层一层(从上往下)遍历
        for(int i = 1; i < m; i++){
            for(int j = 1; j < n; j++){
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }

        return dp[m - 1][n - 1];
        //5. 举例推导dp数组
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

• 时空复杂度
  

lt.63. 不同路径 II

[案例需求]

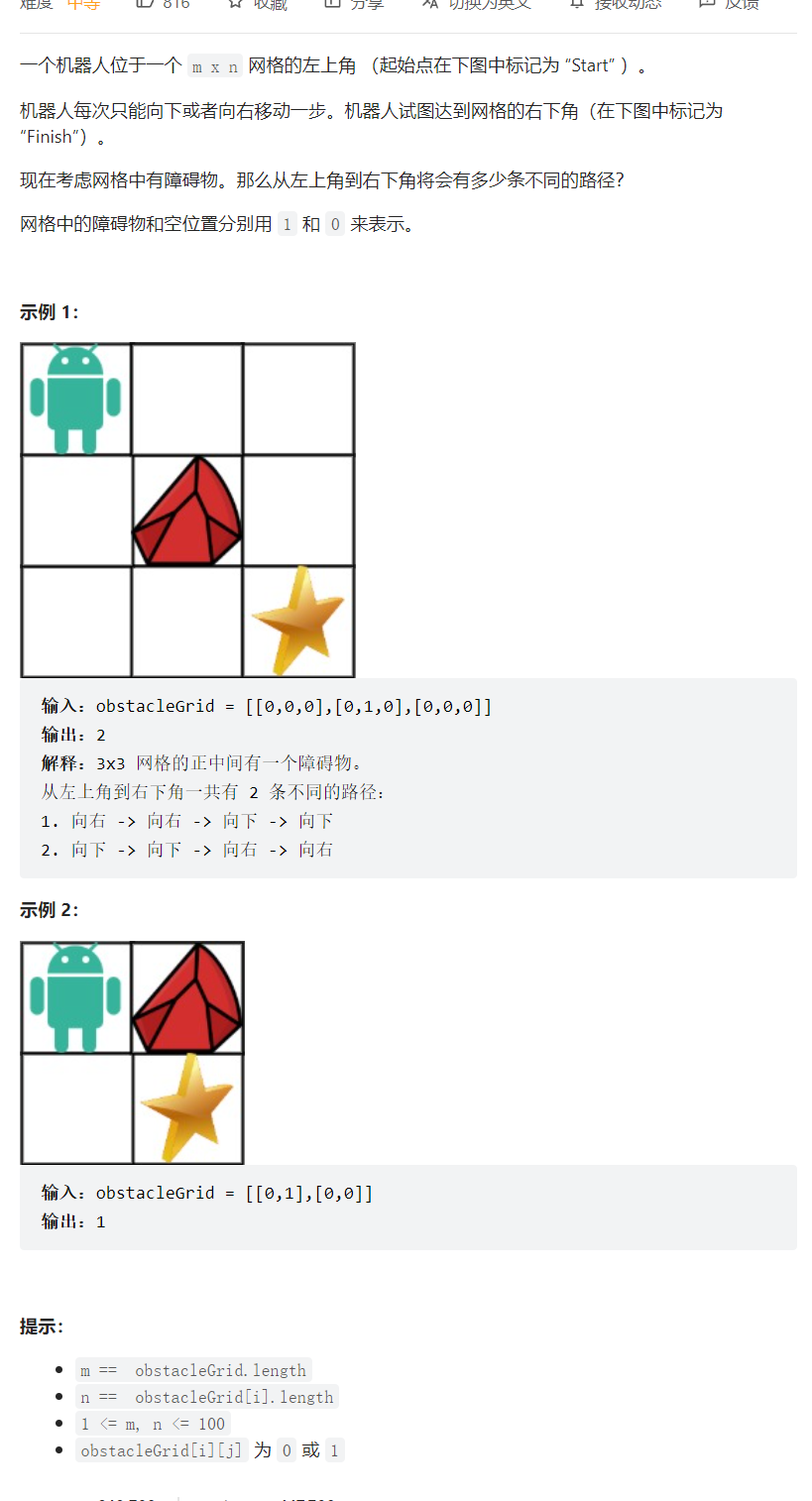
[思路分析]

[代码实现]

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        //1. 确定dp数组的功能并初始化
        //dp[i][j]表示从[0][0] 到[i][j]有多少条路径
        int m = obstacleGrid.length;
        int n = obstacleGrid[0].length;
        //额外的一个剪枝操作
        if(obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1)return 0;


        int[][] dp = new int[m][n];

        //2. 确定递推
        // dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
        //3. 数组的初值. dp[0][j] = 1; dp[i][0] = 1;
        //即 [0][0]到他所在的行或者是列上, 路径都是为1
        //本题设置了障碍, 所以要加上判断(没有障碍的地方才会有初值)
        for(int i = 0; i < m; i++){
            if(obstacleGrid[i][0] == 1)break;
            dp[i][0] = 1;
        }

        for(int j = 0; j < n; j++){
            if(obstacleGrid[0][j] == 1)break;
            dp[0][j] = 1;
        }

        //4. 求值
        for(int i = 1; i < m; i++){
            for(int j = 1; j < n; j++){
                if(obstacleGrid[i][j] != 1){
                    dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
                }
            }
        }

        return dp[m - 1][n - 1];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39