【无人机协同】基于matlab无人飞行器协同车辆物资配送【含Matlab源码 1899期】

一、单车单机映射模式简介

单车单机映射模式（traveling salesman problem with drone，TSP-D）的分析可以基于任新惠提出的无人机和车辆组合配送模式进行分析。

1 无人机和车辆同步配送模式
2015年，Murray和Chu引入了一种新型的旅行商问题，称为“飞行跟班旅行商问题”（flying sidekick traveling salesman problem, FSTSP）。作者提出了在车辆顶部安装一架无人机的想法，该无人机可以在车辆进行一项交付任务的同时进行另一项交付任务。一旦无人机完成交付，它需要在当前交付位置或沿其路线返回车辆到下一个交付位置。由于问题复杂，FSTSP只考虑一辆车辆和一架无人机，如图1所示。Agatz等提出的无人机旅行推销员问题是独立于FSTSP提出的，但仍然共享大多数常见的假设。在这个问题上，FSTSP的一个关键区别是无人机可以在车辆发射的相同位置被找回，并且无人机的操作受到飞行距离而不是时间的限制，然后采用局部搜索与动态规划相结合的算法求解模型。

Bouman等基于贝尔曼-霍尔德-卡普（Bellman-Held-Karp）动态规划算法介绍了一种求解FSTSP的三步精确式方法，并将该方法的最后一步推广到A*算法。此外，他们尝试将这精确式算法应用于限制车辆在与无人机分离时可能访问的位置数量的问题，这个限制导致更短的计算时间，但代价是可能从解空间中移除最优解。Ha等[9]提出了两种启发式方法——贪婪随机自适应搜索（greedy random adaptive search problem, GRASP）和旅行商问题-局部搜索(traveling salesman problem-local search, TSP-LS)启发式求解FSTSP。GRASP元启发式算法首先使用三种不同的启发式算法为车辆生成旅行推销员问题旅行，然后使用分割算法将一些客户从车辆旅行中移除，并将其分配给无人机。TSP-LS启发式算法改编自Murray和Chu提出的启发式算法，但在算法的每次迭代中，在无人机和车辆路线之间重新定位客户所节省的成本计算方面存在差异。在拥有100个客户的问题实例上的实验结果表明，GRASP启发式算法在求解质量上优于TSP-LS启发式算法，尽管它需要更多的计算时间。Es Yurek和Ozmutlu开发了一种基于两阶段分解的算法来求解FSTSP。在第一阶段，使用贪婪启发式方法将客户分配到车辆和无人机上。在第二阶段，求解一个数学规划模型，得到无人机的行程，使无人机在交会点的等待时间最小。Pedro等对FSTSP模型进行了扩展，允许无人机在与车辆的两次连续会合之间每次访问几个客户。除了多点假设之外，他们模型的其他特点是没有为车辆和无人机预先建立路线，并且将每个位置视为它们之间的潜在同步点，然后通过模拟退火算法的全局优化方案，求解了大规模的场景。

综上所述，FSTSP模式中车辆一般配送离供应点较近的需求点，而无人机是辅助车辆进行末端配送，以有效节省总的配送时间和成本。然而，由于无人机在配送过程中依赖于车辆，所以需要考虑在无人机和车辆何处对接，因此对协同性的要求很高，这可以参考传统的拖挂运输问题（truck and trailer routing problem, TTRP）。目前，针对FSTSP模式的研究还停留在基础阶段，较少考虑无人机和车辆对接时存在的实际问题，并且在其问题求解算法中通常基于动态规划的思想分阶段求解无人机和车辆的任务目标，未来需要耦合无人机和车辆的协同任务目标。

2 无人机和车辆并行配送模式
2015年，Murray和Chu除了提出FSTSP之外，文献中还提出车辆和无人机并行调度（parallel drone scheduling traveling salesman problem, PDSTSP），即车辆和无人机从仓库出发独立进行交付，如图2所示。无人机和车辆数量的不同不会对PDSTSP的模式运用带来任何变化，所以本小节不只是基于单车单机模式进行文献回顾，还包括了单车多机、多车多机模式的文献。Ham对PDSTSP问题进行了拓展，其中无人机可以实施连续多阶段的取件和配送任务，解决了多车多机保障多需求点的配送任务分配。Kim和Moon扩展PDSTSP并构建了TSP-DS（traveling salesman problem with a drone station）的MILP模型，考虑了一辆车和多架无人机，以允许无人机独立于车辆、从仓库以及从预先指定的无人机站进行调度，最后发现TSP-DS 比 PDSTSP 更为高效。Chauhan等针对PDSTSP问题的特点，构建了以配送无人机最大航程为直径，以最大范围覆盖用户为目标的仓库选址模型，并以三阶段贪婪算法求解。

由此看出，PDSTSP问题可以分解为两个经典的运筹学问题: TSP和并行机调度问题（parallel machine scheduling problem, PMS）。PDSTSP模式只需要基于上述两个问题考虑如何合理分配客户以实现完工时间最小化，求解难度较小，但其重点是如何判断先进行TSP问题求解还是PMS问题求解，这将会极大影响PSDTSP问题的求解质量。

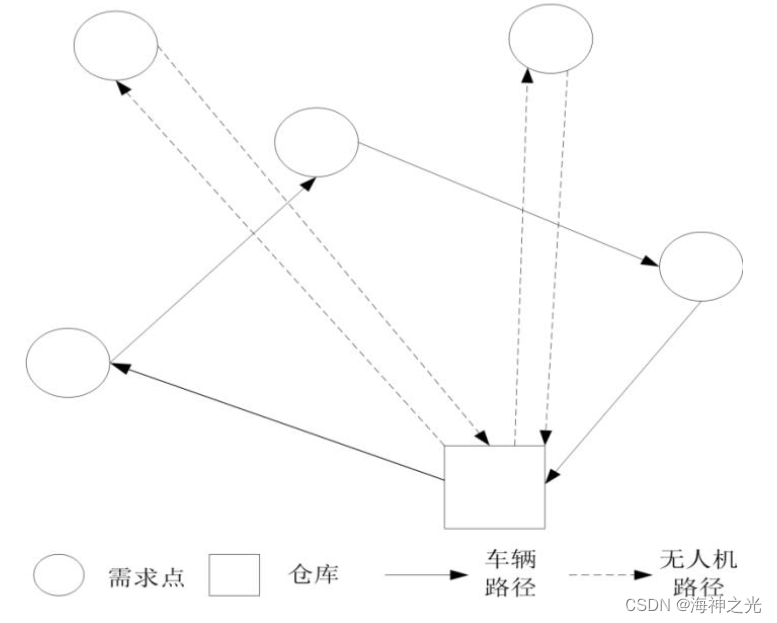
图2 PDSTSP拓扑图

3 车辆保障无人机配送模式
Mathew等在研究多种运输工具配送问题（heterogeneous delivery problem, HDP）首次提出车辆只负责装载配送无人机与需求物资，对所有需求点的配送都由无人机完成，但其模型约束中事先设定了无人机配送的任务点，因此该问题是传统的旅行商问题。

Savuran和Karakaya提出了一个车辆保障无人机配送模式，其目标是通过找到车辆停靠点来发射一架无人机，从而在为所有客户提供服务的同时，最大限度地减少无人机的行驶距离。作者称这个问题为“仓库机动性问题”，因为车辆是无人机的移动仓库。他们开发了一种遗传算法，用一辆车辆和一架无人机来解决一些问题实例，并用最近邻和爬山算法来评估和比较所获得的结果。Othma等基于车辆保障无人机配送模式证明了单车辆和单无人机的多式联运是NP-hard问题，并提出了求解该问题的近似算法。

Luo等[18]在TSP-D的模型构建中，允许无人机单次发射实施多个客户的配送，并考虑了无人机与车辆同时在时间和空间上的协同约束。该问题被公式化为一个MILP模型，描述了一个两级位置路由问题。为了解决这个问题，开发了两种启发式方法，首先构建一个车辆旅行，然后将其分成几个子旅行，将每个子旅行分配给一个无人机。Carlsson和Song考虑将一辆货车携带一架无人机，拓展提出无人机配送的始发点与回收点可在车辆路线上的任一位置，通过连续逼近法找到车辆最佳保障无人机的路线。他们的一个关键发现是无人机与车辆协同使用的潜在好处（提高效率）与无人机和车辆之间的相对速度的平方根相关。

本文将上述这种无人机和车辆组合配送方式称为车辆保障无人机配送模式（vehicle guarantee drone traveling salesman problem, VGDTSP），如图3所示。这种模式属于给定车辆路线的无人机调度问题（drone scheduling problem, DSP）的拓展，并且包括DSP。这一模式适用于车辆无法直达客户地点的城市场景，也适合客户点分散、单位面积物流需求量小、道路条件较差的农村配送。

图3 VGDTSP拓扑图

4 无人机保障车辆配送模式
无人机保障车辆配送模式是指车辆执行配送任务，由无人机作为辅助为车辆补货，这种配送模式主要适用于车辆的途中补货。Dayarian等关注的是无人机补给的同一天交付问题，其中车辆监督交付订单，无人机的作用是向车辆提供补给，并将无人机保障车辆配送模式定义为VRPDR（vehicle routing problem with drone resupply）。最后作者提出了一种启发式方法来解决该问题，但为了简化研究模型，他们考虑了仅有一个配送中心、一辆货车和一架无人机的情况。McCunney和Cauwenberghe假设无人机为车辆提供包裹补给，以实现当天交付服务：无人驾驶飞机将包裹运送到一组预先指定的转运点，每辆车辆从专用转运点提取包裹，为客户所在地的特定区域提供服务，根据订单到达间隔时间、转运点数量、车辆数量和无人机数量的不同值进行综合分析。

二、部分源代码

function sorted_tours = matlabTSPapp(num_stops, bs_x, bs_y, random_seed, app)


%load('usborder.mat','x','y','xx','yy');
rng(3,random_seed) % makes a plot with stops in Maine & Florida, and is reproducible
nStops = num_stops; % you can use any number, but the problem size scales as N^2
stopsLon = zeros(nStops,1); % allocate x-coordinates of nStops
stopsLat = stopsLon; % allocate y-coordinates
n = 1;
while (n <= nStops)
    if n==1
        xp = bs_x;
        yp = bs_y;
    else
        xp = randi([-10 10],1,1);
        yp = randi([-10 10],1,1);
    end
    stopsLon(n) = xp;
    stopsLat(n) = yp;
    n = n+1;
end
%plot(x,y,'Color','red'); % draw the outside border
hold(app.UIAxes);
% Add the stops to the map
plot(app.UIAxes, stopsLon,stopsLat,'*b')
%grid on
%set(gca,'Xtick',-10 : 1 : 10); %sets the numbered ticks 1 apart
%set(gca,'Ytick',-10 : 1 : 10); %same as above
%%%%%

idxs = nchoosek(1:nStops,2);

%%%%%%
dist = hypot(stopsLat(idxs(:,1)) - stopsLat(idxs(:,2)), ...
    stopsLon(idxs(:,1)) - stopsLon(idxs(:,2)));
lendist = length(dist);

%%%%%%
Aeq = spones(1:length(idxs)); % Adds up the number of trips
beq = nStops;

%%%%%%

Aeq = [Aeq;spalloc(nStops,length(idxs),nStops*(nStops-1))]; % allocate a sparse matrix
for ii = 1:nStops
    whichIdxs = (idxs == ii); % find the trips that include stop ii
    whichIdxs = sparse(sum(whichIdxs,2)); % include trips where ii is at either end
    Aeq(ii+1,:) = whichIdxs'; % include in the constraint matrix
end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

三、运行结果

四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.
[3]刘正元,王清华.无人机和车辆协同配送映射模式综述与展望[J].系统工程与电子技术

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除