手把手推导Back Propagation

撰文｜月踏

BP（Back Propagation）是深度学习神经网络的理论核心，本文通过两个例子展示手动推导BP的过程。

1

链式法则

链式法则是BP的核心，分两种情况：

1. 一元方程

在一元方程的情况下，链式法则比较简单，假设存在下面两个函数：

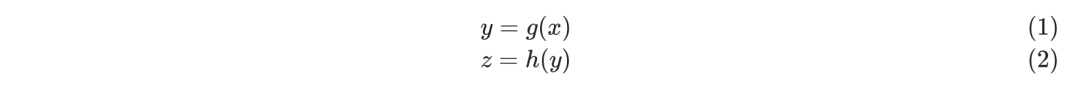
那么x的变化最终会影响到z的值，用数学符号表示如下： 

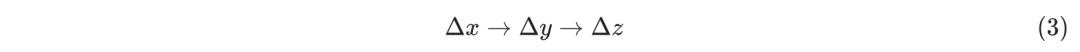
z对x的微分可以表示如下： 

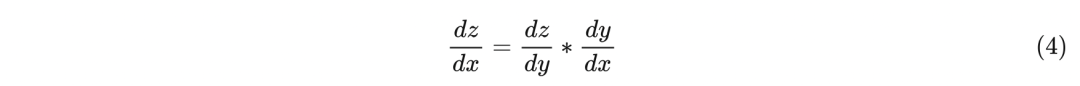
2. 多元方程

在多元方程的情况下，链式法则稍微复杂一些，假设存在下面三个函数： 

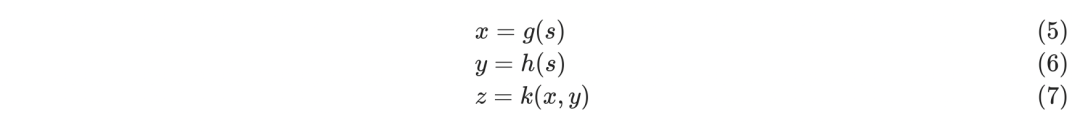
因为s的微小变化会通过g(s)和h(s)两条路径来影响z的结果，这时z对s的微分可以表示如下： 

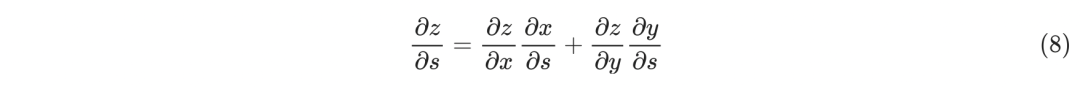
这就是链式法则的全部内容，后面用实际例子来推导BP的具体过程。

2

只有一个weight的简单情况

做了一个简单的网络，这可以对应到链式法则的第一种情况，如下图所示：

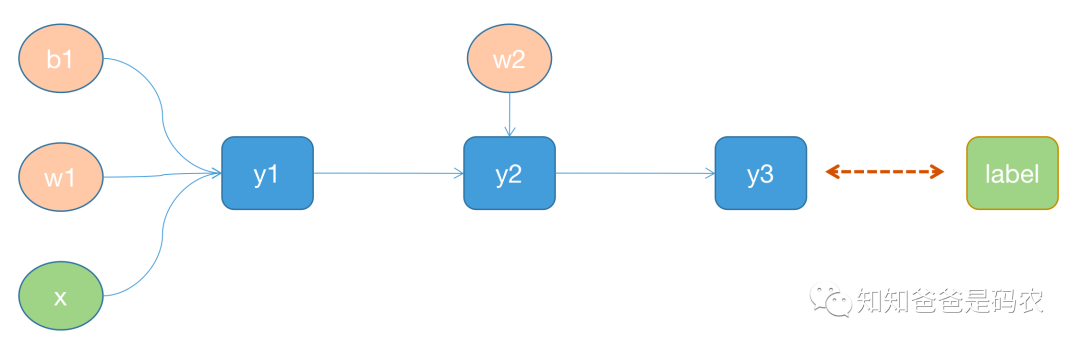
图1

其中圆形表示叶子节点，方块表示非叶子节点，每个非叶子节点的定义如下，训练过程中的前向过程会根据这些公式进行计算： 

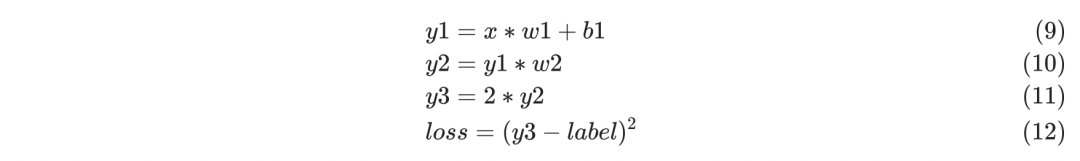
这个例子中，我们是想更新w1、b1、w2三个参数值，假如用lr表示learning rate，那么它们的更新公式如下： 

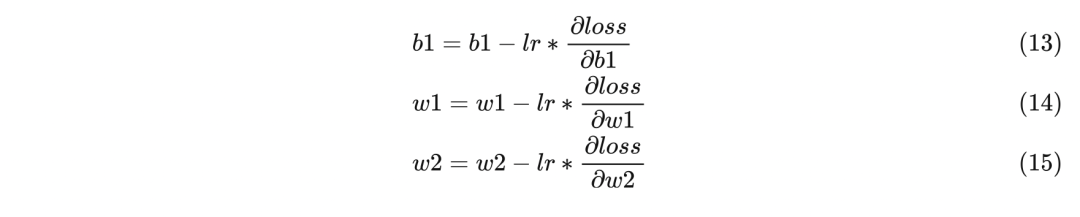
在训练开始之前，b1、w1、w2都会被初始化成某个值，在训练开始之后，参数根据下面两个步骤来进行更新：

1. 先进行一次前向计算，这样可以得到y1、y2、y3、loss的值

2. 再进行一次反向计算，得到每个参数的梯度值，进而根据上面的公式（13）、（14）、（15）来更新参数值

下面看下反向传播时的梯度的计算过程，因为梯度值是从后往前计算的，所以先看w2的梯度计算： 

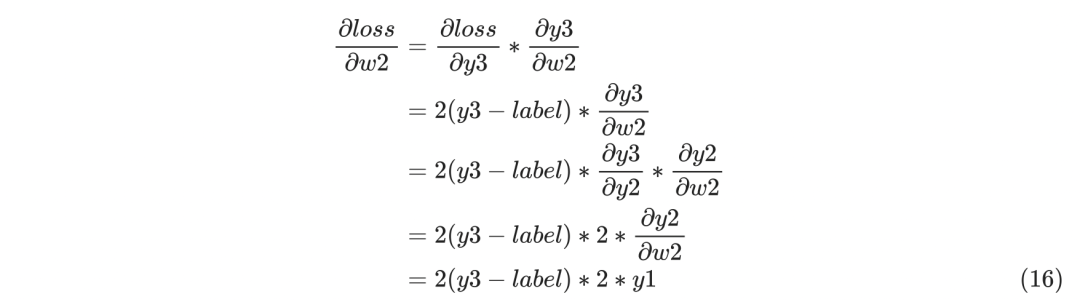
再继续看w1的梯度计算： 

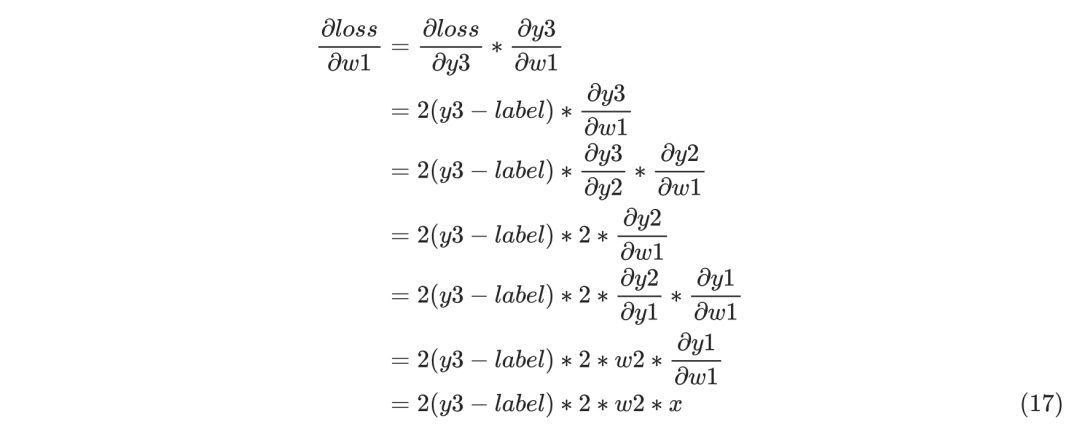
最后看b1的梯度计算： 

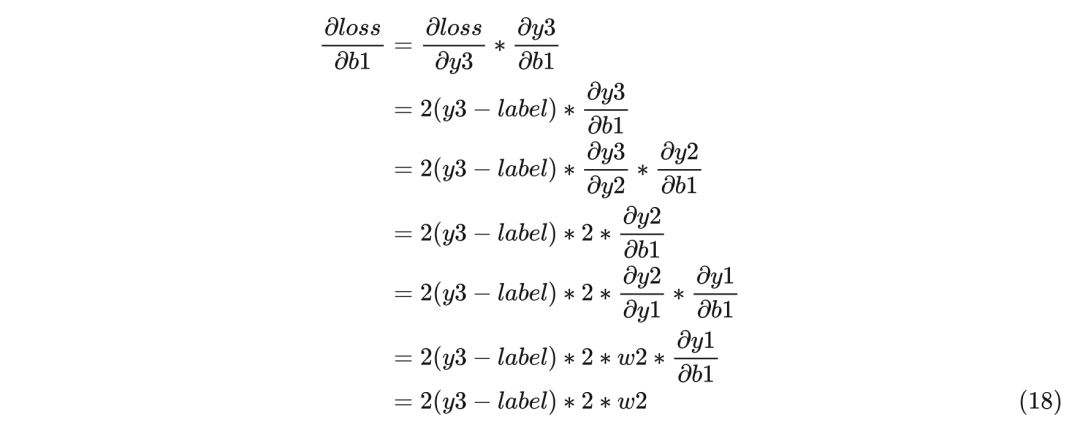
 把w2、w1、b1的梯度计算出来之后，就可以按照公式（13）、（14）、（15）来更新参数值了，下面用OneFlow按照图1搭建一个对应的网络做实验，代码如下：

import oneflow as of
import oneflow.nn as nn
import oneflow.optim as optim
 
 
class Sample(nn.Module):
    def __init__(self):
        super(Sample, self).__init__()
        self.w1 = of.tensor(10.0, dtype=of.float, requires_grad=True)
        self.b1 = of.tensor(1.0, dtype=of.float, requires_grad=True)
        self.w2 = of.tensor(20.0, dtype=of.float, requires_grad=True)
        self.loss = nn.MSELoss()
 
 
    def parameters(self):
        return [self.w1, self.b1, self.w2]
 
 
    def forward(self, x, label):
        y1 = self.w1 * x + self.b1
        y2 = y1 * self.w2
        y3 = 2 * y2
        return self.loss(y3, label)
 
 
model = Sample()
 
 
optimizer = optim.SGD(model.parameters(), lr=0.005)
data = of.tensor(1.0, dtype=of.float)
label = of.tensor(500.0, dtype=of.float)
 
 
loss = model(data, label)
print("------------before backward()---------------")
print("w1 =", model.w1)
print("b1 =", model.b1)
print("w2 =", model.w2)
print("w1.grad =", model.w1.grad)
print("b1.grad =", model.b1.grad)
print("w2.grad =", model.w2.grad)
loss.backward()
print("------------after backward()---------------")
print("w1 =", model.w1)
print("b1 =", model.b1)
print("w2 =", model.w2)
print("w1.grad =", model.w1.grad)
print("b1.grad =", model.b1.grad)
print("w2.grad =", model.w2.grad)
optimizer.step()
print("------------after step()---------------")
print("w1 =", model.w1)
print("b1 =", model.b1)
print("w2 =", model.w2)
print("w1.grad =", model.w1.grad)
print("b1.grad =", model.b1.grad)
print("w2.grad =", model.w2.grad)
optimizer.zero_grad()
print("------------after zero_grad()---------------")
print("w1 =", model.w1)
print("b1 =", model.b1)
print("w2 =", model.w2)
print("w1.grad =", model.w1.grad)
print("b1.grad =", model.b1.grad)
print("w2.grad =", model.w2.grad)

这段代码只跑了一次forward和一次backward，然后调用step更新了参数信息，最后调用zero_grad来对这一轮backward算出来的梯度信息进行了清零，运行结果如下：

------------before backward()---------------
w1 = tensor(10., requires_grad=True)
b1 = tensor(1., requires_grad=True)
w2 = tensor(20., requires_grad=True)
w1.grad = None
b1.grad = None
w2.grad = None
------------after backward()---------------
w1 = tensor(10., requires_grad=True)
b1 = tensor(1., requires_grad=True)
w2 = tensor(20., requires_grad=True)
w1.grad = tensor(-4800.)
b1.grad = tensor(-4800.)
w2.grad = tensor(-2640.)
------------after step()---------------
w1 = tensor(34., requires_grad=True)
b1 = tensor(25., requires_grad=True)
w2 = tensor(33.2000, requires_grad=True)
w1.grad = tensor(-4800.)
b1.grad = tensor(-4800.)
w2.grad = tensor(-2640.)
------------after zero_grad()---------------
w1 = tensor(34., requires_grad=True)
b1 = tensor(25., requires_grad=True)
w2 = tensor(33.2000, requires_grad=True)
w1.grad = tensor(0.)
b1.grad = tensor(0.)
w2.grad = tensor(0.)

3

以conv为例的含有多个weights的情况

用一个非常简单的conv来举例，这个conv的各种属性如下：

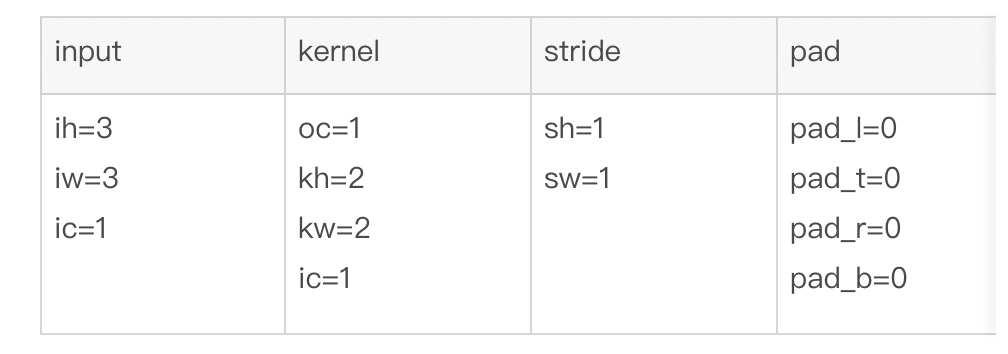
如下图所示：

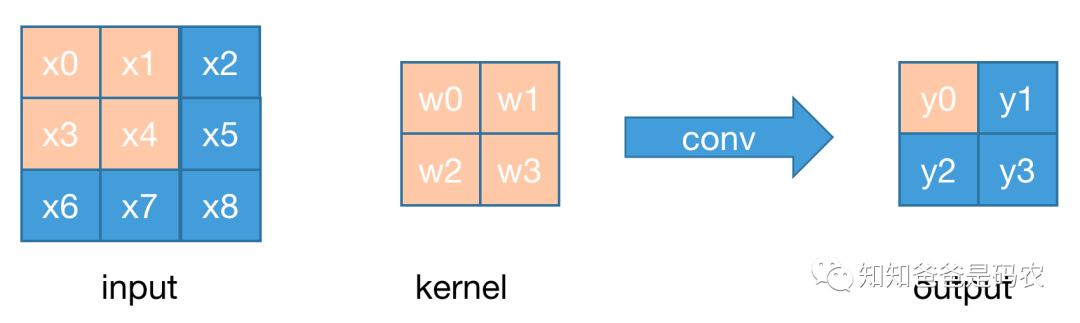
图2

假定这个例子中的网络结构如下图：

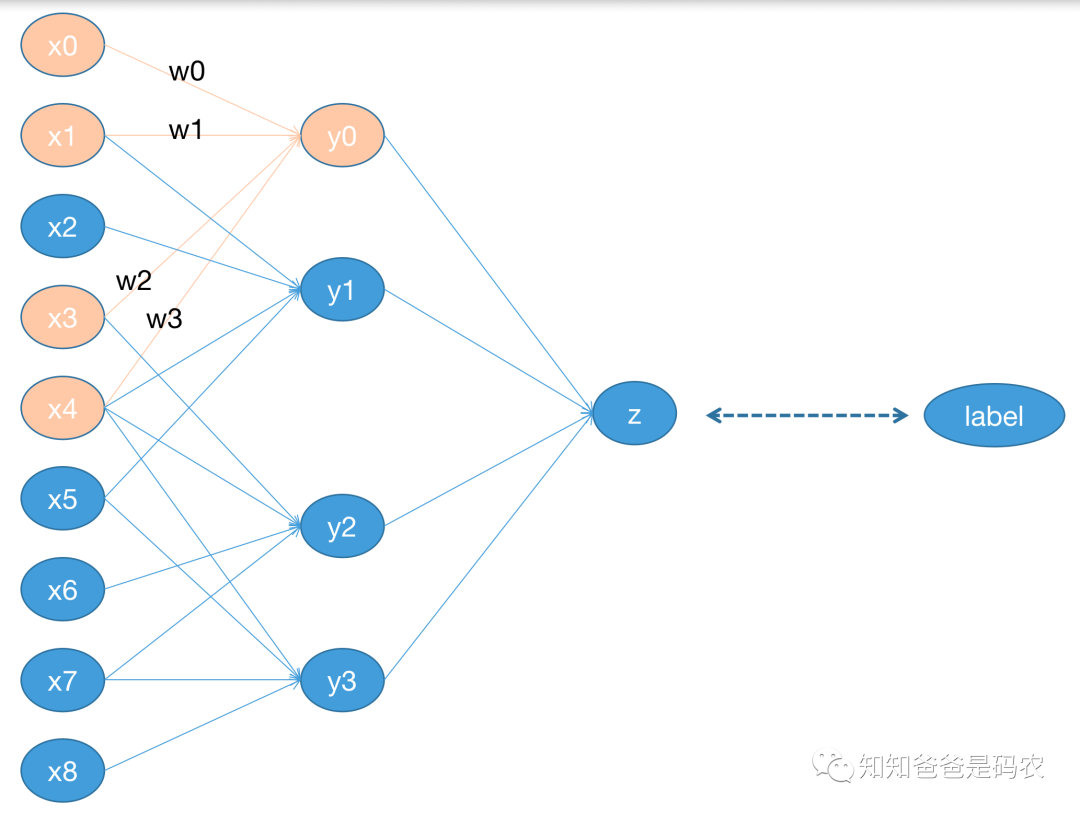
图3

在这个简单的网络中，z节点表示一个avg-pooling的操作，kernel是2x2，loss采用均方误差，下面是对应的公式：

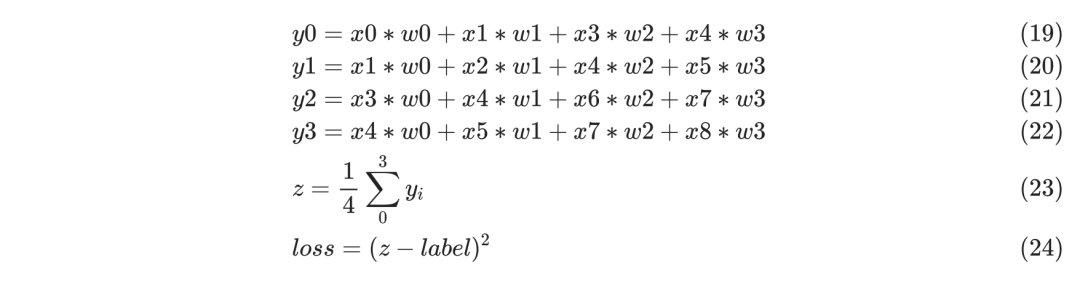
前传部分同上一节一样，直接看反传过程，目的是为了求w0、w1、w2、w3的梯度，并更新这四个参数值，以下是求w0梯度的过程： 

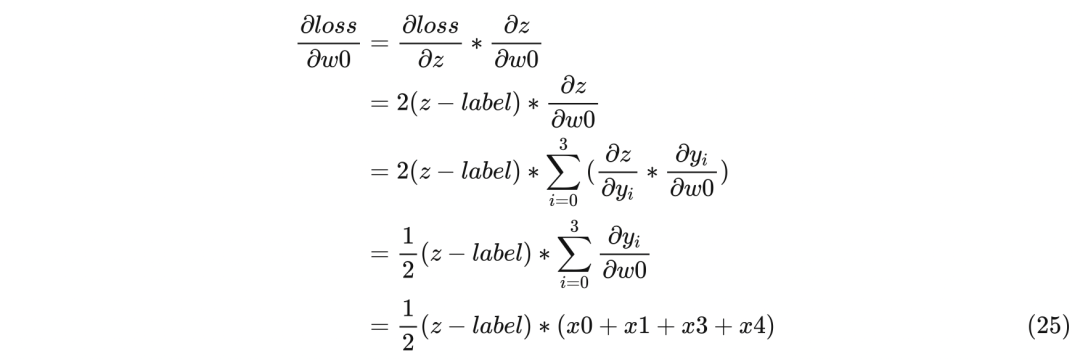
下面是求w1、w2、w3梯度的过程类似，直接写出结果：

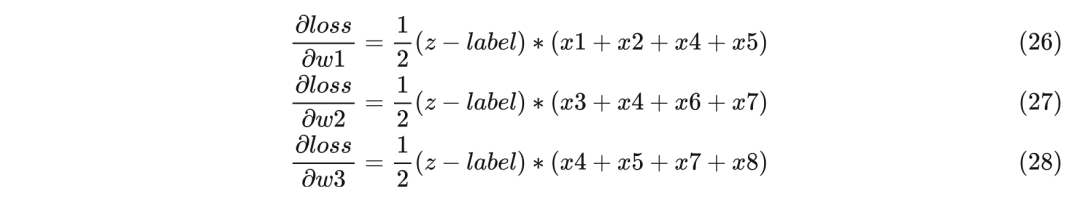
最后再按照下面公式来更新参数即可： 

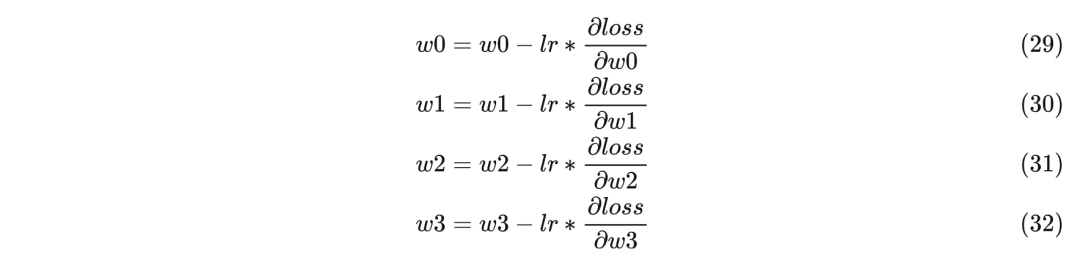
用OneFlow按照图3来搭建一个对应的网络做实验，代码如下：

import oneflow as of
import oneflow.nn as nn
import oneflow.optim as optim
 
 
class Sample(nn.Module):
    def __init__(self):
        super(Sample, self).__init__()
        self.op1 = nn.Conv2d(in_channels=1, out_channels=1, kernel_size=(2,2), bias=False)
        self.op2 = nn.AvgPool2d(kernel_size=(2,2))
        self.loss = nn.MSELoss()
 
 
    def forward(self, x, label):
        y1 = self.op1(x)
        y2 = self.op2(y1)
        return self.loss(y2, label)
 
 
model = Sample()
 
 
optimizer = optim.SGD(model.parameters(), lr=0.005)
data = of.randn(1, 1, 3, 3)
label = of.randn(1, 1, 1, 1)
 
 
loss = model(data, label)
print("------------before backward()---------------")
param = model.parameters()
print("w =", next(param))
loss.backward()
print("------------after backward()---------------")
param = model.parameters()
print("w =", next(param))
optimizer.step()
print("------------after step()---------------")
param = model.parameters()
print("w =", next(param))
optimizer.zero_grad()
print("------------after zero_grad()---------------")
param = model.parameters()
print("w =", next(param))

输出如下（里面的input、param、label的值都是随机的，每次运行的结果会不一样）：

------------before backward()---------------
w = tensor([[[[ 0.2621, -0.2583],
          [-0.1751, -0.0839]]]], dtype=oneflow.float32, grad_fn=<accumulate_grad>)
------------after backward()---------------
w = tensor([[[[ 0.2621, -0.2583],
          [-0.1751, -0.0839]]]], dtype=oneflow.float32, grad_fn=<accumulate_grad>)
------------after step()---------------
w = tensor([[[[ 0.2587, -0.2642],
          [-0.1831, -0.0884]]]], dtype=oneflow.float32, grad_fn=<accumulate_grad>)
------------after zero_grad()---------------
w = tensor([[[[ 0.2587, -0.2642],
          [-0.1831, -0.0884]]]], dtype=oneflow.float32, grad_fn=<accumulate_grad>)

参考资料：

1.http://speech.ee.ntu.edu.tw/~tlkagk/courses.html

2.https://speech.ee.ntu.edu.tw/~hylee/index.php

3.https://www.youtube.com/c/HungyiLeeNTU

其他人都在看

• 25倍性能加速，OneFlow“超速”了

• 一个GitHub史上增长最快的AI项目

• 手把手推导Ring All-reduce的数学性质

• DeepMind爆发史：决定AI高峰的“游戏玩家”

• 解读Pathways（二）：向前一步是OneFlow

• 五年ML Infra生涯，我学到最重要的3个教训

• OneFlow v0.7.0发布：全新分布式接口，LiBai、Serving等一应俱全

欢迎下载体验OneFlow v0.7.0：GitHub - Oneflow-Inc/oneflow: OneFlow is a performance-centered and open-source deep learning framework.https://github.com/Oneflow-Inc/oneflow