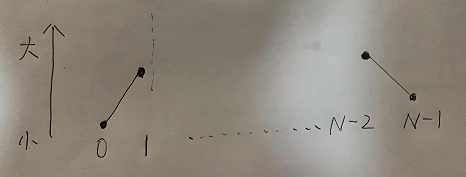作者:Grey
原文地址:使用二分法来解决的问题
在一个有序数组中,找某个数是否存在#
OJ见:LeetCode 704. Binary Search
思路:
- 先得到中点位置,中点可以把数组分为左右半边。
- 如果中点位置的值等于目标值,直接返回中点位置。
- 如果中点位置的值小于目标值,则去数组左边按同样的方式寻找。
- 如果中点位置的值大于目标值,则取数组右边按同样的方式寻找。
- 如果最后没有找到,则返回:-1。
代码
class Solution {
public int search(int[] nums, int target) {
if(nums == null || nums.length < 1) {
return -1;
}
int l = 0;
int r = nums.length - 1;
while (l <= r) {
int mid = l + ((r - l)>>1);
if (target > nums[mid]) {
l = mid + 1;
} else if (target == nums[mid]) {
return mid;
} else {
r = mid - 1;
}
}
return -1;
}
}
在一个有序数组中,找大于等于某个数最左侧的位置#
OJ见:牛客-查找某个位置
这个问题只需要在上例基础上进行简单改动即可,上例中,我们找到满足条件的位置就直接return了
if (target == nums[mid]) {
return mid;
}
在本问题中,因为要找到最左侧的位置,所以,在遇到相等的时候,只需要先把位置记录下来,不用直接返回,然后继续去左侧找是否还有满足条件的位置。
同时,在遇到target < nums[mid]条件下,也需要记录下此时的mid位置,因为这也可能是满足条件的位置。
代码:
import java.util.Arrays;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int k = in.nextInt();
int[] arr = new int[n];
for (int i = 0; i < n; i++) {
arr[i] = in.nextInt();
}
// 虽然不排序也可以通过,但是题目未说明一定是有序数组
Arrays.sort(arr);
System.out.println(getNearestLeft(arr, k));
in.close();
}
public static int getNearestLeft(int[] nums, int target) {
if (nums == null || nums.length < 1) {
return -1;
}
int l = 0;
int r = nums.length - 1;
int ans = 0;
while (l <= r) {
int mid = l + ((r - l) >> 1);
if (target < nums[mid]) {
ans = mid;
r = mid - 1;
} else if (target > nums[mid]) {
l = mid + 1;
} else {
ans = mid;
r = mid - 1;
}
}
return ans;
}
}
LeetCode上有很多类似的问题,都可以用如上方式解答,比如:
LeetCode 35. Search Insert Position
代码见:LeetCode_0035_SearchInsertPosition
LeetCode 34. Find First and Last Position of Element in Sorted Array
代码见:LeetCode_0034_FindFirstAndLastPositionOfElementInSortedArray
局部最大值问题#
OJ见:LeetCode 162. Find Peak Element
思路
假设数组长度为N,首先判断0号位置的数和N-1位置的数是不是峰值位置。
0号位置只需要和1号位置比较,如果0号位置大,0号位置就是峰值位置。
N-1号位置只需要和N-2号位置比较,如果N-1号位置大,N-1号位置就是峰值位置。
如果0号位置和N-1在上轮比较中均是最小值,那么数组的样子必然是如下情况:
[0..1]区间内是增长, [N-2...N-1]区间内是下降
那么峰值位置必在[1...N-2]之间出现
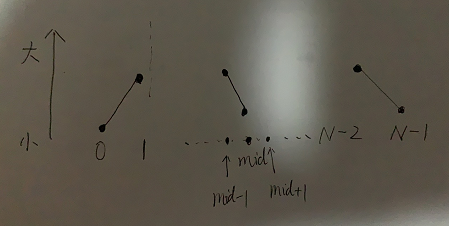
此时可以通过二分来找峰值位置,先来到中点位置,假设为mid,如果:
arr[mid] > arr[mid+1] && arr[mid] > arr[mid-1]
则mid位置即峰值位置
否则,有如下两种情况:
情况一,趋势是:
则在[1...(mid-1)]区间内继续上述二分。
情况二,趋势是:
则在[(mid+1)...(N-2)]区间内继续上述二分。
完整代码
public class LeetCode_0162_FindPeakElement {
public static int findPeakElement(int[] nums) {
if (nums.length == 1) {
return 0;
}
int l = 0;
int r = nums.length - 1;
if (nums[l] > nums[l + 1]) {
return l;
}
if (nums[r] > nums[r - 1]) {
return r;
}
l = l + 1;
r = r - 1;
while (l <= r) {
int mid = l + ((r - l) >> 1);
if (nums[mid] > nums[mid + 1] && nums[mid] > nums[mid - 1]) {
return mid;
}
if (nums[mid] < nums[mid + 1]) {
l = mid + 1;
} else if (nums[mid] < nums[mid - 1]) {
r = mid - 1;
}
}
return -1;
}
}
分割数组的最大值#
给定一个非负整数数组 nums 和一个整数 m ,你需要将这个数组分成 m 个非空的连续子数组。设计一个算法使得这 m 个子数组各自和的最大值最小。
OJ见:LeetCode 410. Split Array Largest Sum
PS: 此题也可以用四边形不等式优化的动态规划来解,但是最优解是二分法
思路
我们先求整个数组的累加和,假设累加和为sum,我们可以得到一个结论,分割的m个非空连续子数组的和的范围一定在(0,sum]区间内。转换一下思路,如果某种划分下的子数组之和的最大值为max,则max首先肯定在(0,sum]区间内。思路转换为:
子数组的累加和最大值不能超过max的情况下,最少可分多少部分?
假设能分k个部分,
如果k <= m,说明这种划分是满足条件的,我们看max是否可以变的更小。
如果k > m,说明这种划分是不满足条件的,我们需要调大max的值。
这里可以通过二分的方式来定位max的值。即max先取(0,sum]的中点位置,得到的划分部分k如果k <= m,则max继续去左边取中点位置来得到新的划分k,
如果k > m,max继续从右边的中点位置来得到新的划分k。
完整代码
class Solution {
public static int splitArray(int[] nums, int m) {
int sum = 0;
for (int num : nums) {
sum += num;
}
int l = 0;
int r = sum;
int ans = 0;
while (l <= r) {
int mid = l + ((r - l) >> 1);
int parts = getParts(nums, mid);
if (parts > m) {
// mid越大,parts才会越小
l = mid + 1;
} else {
ans = mid;
r = mid - 1;
}
}
return ans;
}
// 达到aim要分几部分
public static int getParts(int[] nums, int aim) {
for (int num : nums) {
if (num > aim) {
return Integer.MAX_VALUE;
}
}
int part = 1;
int all = nums[0];
for (int i = 1; i < nums.length; i++) {
if (all + nums[i] > aim) {
part++;
all = nums[i];
} else {
all += nums[i];
}
}
return part;
}
}
其中:int getParts(int[] nums, int aim)方法表示,在不超过aim的情况下,最少需要几个划分部分。方法的主要逻辑是:
遍历数组,如果发现某个元素的值超过了aim,直接返回系统最大,说明无法得到划分。如果没有超过aim,则继续加入下一个元素,直到超过aim,就定位出一个部分。依次类推,就可以得到最少有几个划分。
判断一个数是否是Step Sum#
何为step sum? 比如680,680 + 68 + 6 = 754,所以680的Step Sum是754,给定一个正数num,判断它是不是某个数的Step Sum。
使用二分法来解决这个问题,思路如下:
如果一个数x的Step Sum为m,另外一个数y的Step Sum为n,如果x大于y,则m一定大于n。
给定一个数num,我们可以求0到num的中点位置mid,看这个位置的Step Sum是不是给定的num,如果是,直接返回true,如果中点位置的Step Sum大于num,则考虑在左半边继续二分,如果中点位置的Step Sum小于num,则考虑在右半边继续二分。
public class Code_0111_IsStepSum {
public static boolean isStepSum(int stepSum) {
int i = 0;
int j = stepSum;
while (i <= j) {
int mid = i + ((j - i) >> 1);
int value = stepSumOf(mid);
if (value == stepSum) {
return true;
} else if (value < stepSum) {
i = mid + 1;
} else {
// value > stepSum
j = mid - 1;
}
}
return false;
}
public static int stepSumOf(int num) {
int v = 0;
while (num != 0) {
v += num;
num = num / 10;
}
return v;
}
}