长这样:
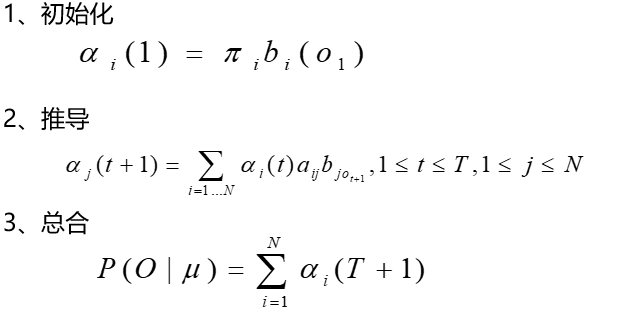
理解的前提:

(1)状态:生成观测值的变量(上图中的“吃”和“睡”)。
(2)观测值:状态乘上输出概率对应的输出(上图中的橙色节点)。
(3)输出概率:输出概率矩阵里面的某个元素(状态和观测值两层之间的某个权重参数)。
(4)输出概率矩阵:由输出概率组成的矩阵。
(5)bi: 第i个状态(比如”睡“)输出所有观测值对应的概率构成的行向量(上图中所有红线构成的行向量)。
(6)o1:表示我要输出第一个观测值。不是把o1做为自变量输入到bi中,只是一个记号(个人表示没什么用)。
(7)Πi:走 第i个状态的初始概率(p(start->吃)=0.3)。
(8)αi(t):(阿尔法)在给定马尔可夫模型中,到t时刻为止,状态们在t个时刻,每个时刻都由所有状态中的一个输出某个观测值,一共输出了t个观测值观测序列,记为,
,并且t时刻输出Ot的状态为qi(状态用q表示),把出现上述场景的概率记作αi(t),称作前向概率(应该是在做前向计算,所以形象成为”前向概率“)。

(9)aij:(字母a,注意不是阿尔法,在第一张图中的“推导”公式里面的)概率转移矩阵中第i行,第j列对应的概率(今天为第i个状态,明天为第j个状态的概率。网络图示中“吃->吃”、“吃->睡”和“睡->睡”之间连线的数 值)。
(10)转移概率矩阵:如下图A所示。

理解
 :
:
表示第1时刻,第i个状态的初始概率Πi乘以第i个状态对应的输出矩阵的第i行向量。
例如:假设第i个状态为“睡”,那么Πi等于0.7,bi等于[0.3,0.5,0.2],那么第1时刻的状态为“睡”,观测值为“哭”、“没精神”和“找妈妈”的概率分别为0.7*[0.3,0.5,0.2],如果第一时刻的观测值为“哭”,那么α1(t)=0.21.
![]() :
:
t+1时刻,所有t时刻的前向概率里面按时的t时刻的状态转化为j状态后再乘以j对应的输出概率总和。
以第2时刻为例:状态j为“吃”,那么αj(t+1)表示第二时刻,第二状态为“吃”,观测值序列为的O1O2概率,其等于第1时刻的前向概率αi(t) 乘以 第一时刻的前向概率里面暗示的第一时刻的状态i转化为状态j的概率(aij),i有可能是“吃”,也有可能是“睡”,我们要计算的是第2时刻状态为“吃”的概率,根据马尔可夫模型,第二时刻的“吃”和第一时刻的状态有关,但是我们不知道第一时刻到底是什么状态,所以用概率的方式全部考虑进来。
[0.21,0.03,0.02]*0.1*bjo2(0.1表示“吃1”->“吃2”的概率)+[0.21,0.15,0.14]*0.9*bjo2(0.9表示“睡1”->“吃2”的概率)
乘上转移概率之后,在乘以“吃”对应的输出概率行向量:
[0.021,0.003,0.002]Tx[0.7,0.1,0.2] + [0.189,0.135,0.126]Tx[0.7,0.1,0.2](考虑了所有情况,可能会有点费解,请看下一行)
如果第一时刻的观测值为“哭”,第二时刻的状态为“吃”,观测值为“哭”,那么αj(t+1)=0.21*0.1*0.7=0.0147 + 0.21*.0.9*0.7=0.1323.
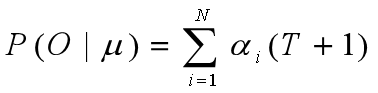 :
:
μ:给定的马尔可夫模型。
O:1-T+1时刻的观测值序列。
在马尔可夫模型μ中,输出序列O的概率为:输出O并且T+1时刻的状态为qi的概率综合。
本文截图部分来自:隐马尔科夫模型(HMM)一前向与后向算法 - 知乎 (zhihu.com)