南京邮电大学统计学课程实验2 用EXCEL进行参数估计假设检验 指导

一、实验描述 

• 实验目的

1、学会用Excel进行参数估计；

2、学会用Excel进行z检验-双样本平均差检验；

• 实验环境

实验中使用以下软件和硬件设备

（1）Windows XP操作系统；

（2）PC机、EXCEL软件；

• 实验内容和步骤

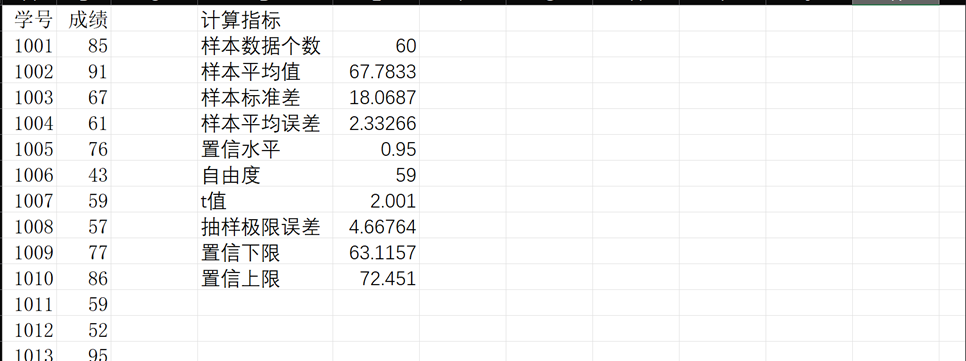
1、某学校为了了解一次期末考试中，某年级的期末考试的英语成绩，随机抽取了60名同学期末考试成绩如下，求在概率95%的保证下，该年级同学期末考试英语平均成绩的置信区间。（参数估计指标包括：样本数；样本平均值；样本标准差；样本平均误差；置信水平；自由度；t值；抽样极限误差；置信上下限）

1.实验步骤：

（1）针对题中所有数据，使用COUNT函数进行计算，得到样本数据总数为60；

（2）针对题中所有数据，使用AVERAGE函数进行计算，得到样本平均值为67.7833；

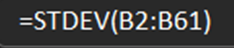
（3）针对题中所有数据，使用STDEV函数进行计算，得到样本标准差为18.0687；

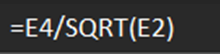
（4）结合样本标准差为18.0687和样本数据总数为60，使用样本标准差除以根号下样本数据个数，即可得到样本标准误差为2.33266；

 (5)由于题中所述要求概率在95%以上，所以可得置信水平为0.95；

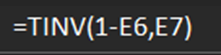
(6)结合样本数据总数为60，样本自由度为样本总数-1=59；

（7）结合样本置信水平为0.95和样本自由度为59，使用TINV函数进行计算，即可得到所求样本数据的t值为2.001；

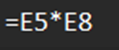
(8)结合样本平均误差为2.33266和t值为2.001，使用样本平均误差与t值相乘，即可得到抽样极限误差为4.66764；

(9)结合样本平均值为67.7833和抽样极限误差为4.66764，即可得到置信下限为样本平均值-抽样极限误差=63.11569；

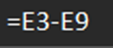
(10)结合样本平均值为67.7833和抽样极限误差为4.66764，即可得到置信上限为样本平均值+抽样极限误差=72.451。

该样本数据集的参数估计指标

2.结论分析：

结合EXCEL的数据分析手段，使用相应函数语句调令，可得如上十项参数估计指标来评估该年级同学期末考试英语成绩。并由此分析可知，置信水平为0.95的条件下，该样本数据的置信下限为63.1157，置信上限为72.451。即在概率95%的保证下，该年级同学期末考试英语平均成绩的置信区间为（63.1157,72.451）。

2、为了比较1、2两个班级同学身高的差异，随机各选取了30名同学进行比较

根据以往经验知身高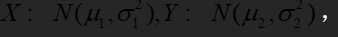，且方差都为6，试在的显著性水平下比较两班学生的身高有无显著差别。

1. 实验步骤：

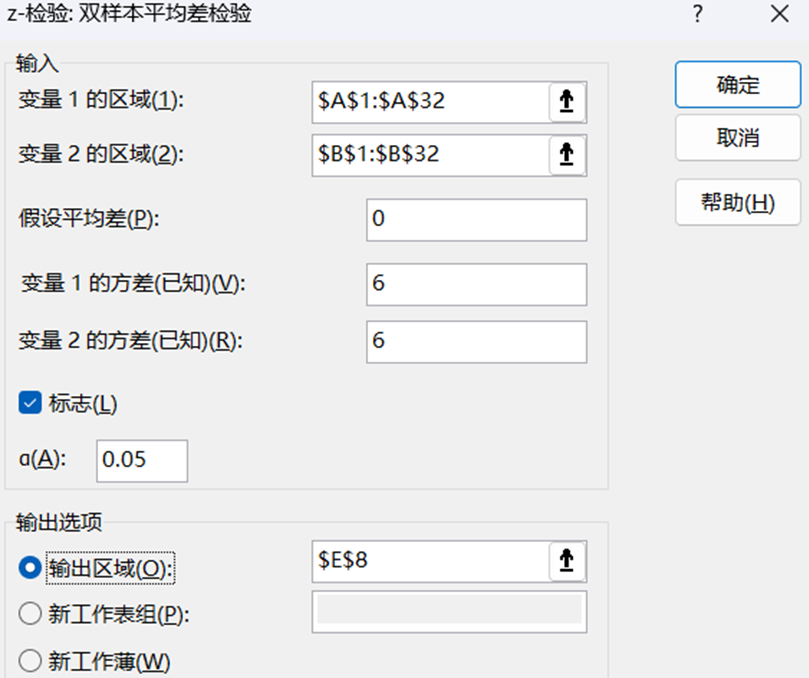
1）将题目数据导入EXCEL表格中，然后调用数据分析功能模块中的“z-检验：双样本平均差检验”。

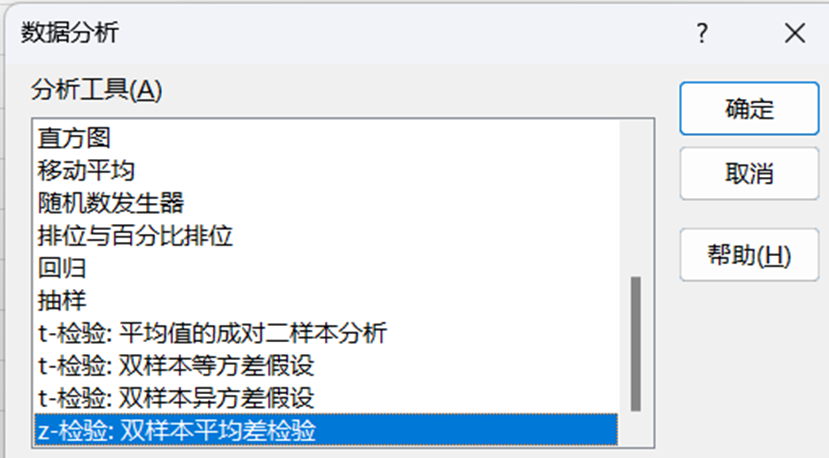
2）结合题中所述的方差为6和置信度为0.05，在z-检验中填入相关信息，即可进行z-分析求解。

3）电脑进行z-检验，可得实验结果如下图：

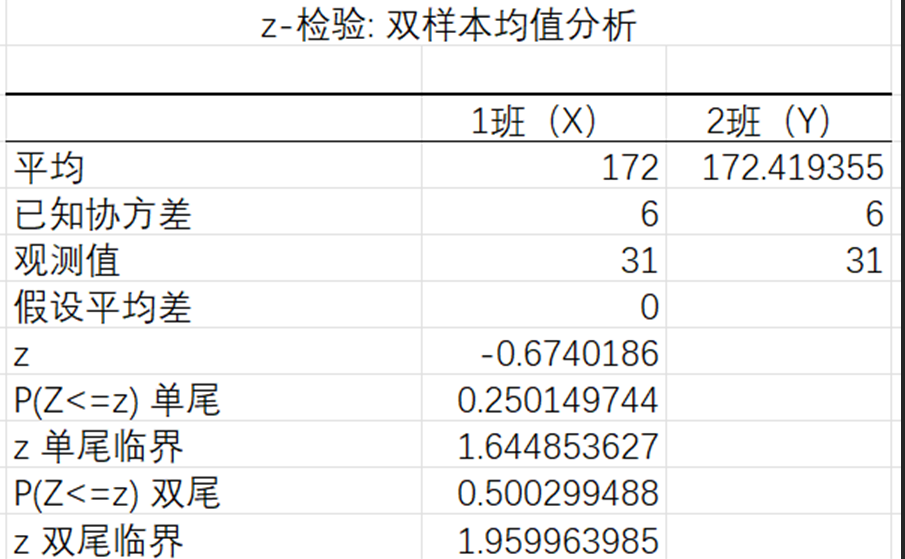
 2.结论分析：

在本题提供的数据中，两个班级的身高平均数非常接近，而且样本量也比较大，因此可以使用z-检验来进行假设检验。在这个例子问题中，假设平均差为0，得到的z值为-0.674，表示样本的平均值距离假设平均值差了0.674个标准差。同时，p值为0.5003，表示双尾检验下拒绝原假设的显著性水平为0.5 > 0.05，故无法拒绝原假设。根据这个结果可以认为，在α=0.05的显著性水平下，两个班级学生的身高没有显著差异。