【推荐算法】召回模型总结

1、传统召回算法

• 详见链接：https://blog.csdn.net/m0_48086806/article/details/136914225

2、向量化召回统一建模架构

• 向量化召回的思想就是将召回问题建模为向量空间的紧邻搜索问题。
• 假设召回问题中包含两类实体Q和T

1）Q是用户，T是物料，为用户直接找喜欢的物料，就是user-to-item（U2I）召回
2）Q和T都是物料，为用户找与他喜欢物料相似的其他物料，就是item-to-item（I2I）召回
3）Q和T都是用户，先为当前用户查找与他相似的用户，再把相似用户喜欢的物料推荐给当前用户，就是user-to-user-item（U2U2I）召回

• 向量化召回的基本步骤如下：

1）训练一个模型M，将Q中的每个实例q和T中的每个实例t映射到同一个向量空间
2）将T中所有实例映射成向量，并存入向量数据库，建立索引
3）在线服务时，对于Q中的一个实例q，通过M映射为向量$Em{b}_q$。再在向量数据库中，通过近似最近邻ANN搜索算法，查找与$Em{b}_q$最近的K个T类的邻居向量作为召回结果

• 向量化召回是一类算法家族：例如Item2Vec、Youtube召回算法、Airbnb召回、FM召回、微软DSSM、双塔模型、百度孪生网络、阿里巴巴的EGES、腾讯的GraphTR等。
• 向量化召回的4个维度：

1）如何定义正样本，即哪些q和t在向量空间是相近的
2）如何定义负样本，即哪些q和t在向量空间是较远的
3）如何将q和t映射成Embedding，模型本身
4）如何定义优化目标，即损失函数

2.1、如何定义正样本

• 三种场景下的正样本定义方式：

I2I 召回。q和t都是物料。比如认为同一个用户在同一个会话(session，闻隔时间较短的用户行为序列)交互过(例如点击、观看、购买等)的两个物料，在向量空间是相近的。这体现的是两个物料的相似性。

U2I召回。q是用户，t是物料。一个用户与其交互过的物料在向量空间中应该是相近的。
这体现的是用户与物料的匹配性。

U2U 召回。q和t都是用户。比如使用孪生网络，q是用户一半的交互历史，t是同一用户另一半交互历史，二者在向量空间应该是相近的，这体现的是同一性。

2.2、重点关注负样本

• 首先，需要注意的一点是排序和召回所面临的候选集物料的分布是不同的

排序：所面对的候选物料是已经和用户兴趣比较匹配的优质集合。
召回：是将用户可能喜欢的和海量跟用户兴趣不相关的物料分隔开，所以，召回
所面对的候选物料集合可谓“鱼龙混杂，良莠不齐”。

• 所以，对喂入召回模型的样本的要求是，既要让模型见过最匹配的(user，item)组合，也要让模型见过最不靠谱的(user，item)组合，这样才能让模型达到“开眼界、见世面”的目的，从而在“大是大非”上不犯错误。
• 因此负样本不能只用曝光未点击的样本，要进行随机负采样，特别是在 U2I召回场景中，坚决不能(只)拿“曝光未点击”样本作为负样本。
• 随机负采样中的关键点如下：

1）推荐系统中不可避免的存在“二八定律”，即20%的热门物料占据了80%的曝光流量。那么U2I、I2I召回中，正样本的的物料以少数热门物料为主，可能带偏模型对所有用户只推荐热门物料。因此需要进行纠偏，例如在FM中，热门物料在正样本中要降采样

2）最简单的负采样方法是在所有物料组成的大库中进行随机采样，但代价太高，更是无法满足在线学习的实时性要求。因此业界也提出了许多近似的折中方案，例如双塔模型中的Batch内负采样和混合负采样

3）进一步考虑，负样本可以分为易分负样本（Easy Negative）和难分负样本（Hard Negative），例如q是一只狗的图片时，负样本如果是猫、大象、乌鸦、海豚，与q相差很大，属于易分负样本；负样本如果是狼、狐狸，属于难分负样本。

• 因此，难分负样本可以作为易分负样本的补充，在数量上，负样本还是应该以 EasyNegative为主，Facebook的经验是将比例维持在 Easy:Hard=100:1。毕竟在线召回时，候选集中的绝大多数物料都是与用户毫不相关的，保证 Easy Negative 的数量优势才能保持召回模型的基本精度。

• 总之，如果说排序是特征的艺术,那么召回就是样本的艺术,特别是负样本的艺术。做召回,“负样本为王”,负样本的选择对于算法成败是决定性的:选对了，模型基本合格;选错了，之后的特征工程、模型设计、推理优化都是南辕北辙，平添无用功罢了。

2.3、召回生成Embedding：要求用户、物料解耦

• 最重要的一点：排序鼓励交叉，召回要求解耦
• 排序由于其候选集规模比较小，因此可以鼓励交叉，而召回面对的候选集规模太大，如果每个用户与每个候选物料都进行交叉，其实时性要求很难保证
• 所以，召回必须解耦，隔离用户信息与物料信息。

特征策略上，召回无法使用用户与物料的交叉统计特征(如用户标签与物料标签的重合度)

模型结构上，召回必须各自处理用户特征和物料特征。用户子模型只利用用户特征，生成用户向量$Em{b}_{user}$。物料子模型只利用物料特征，生成物料向量$Em{b}_{item}$。只允许最后计算 $Em{b}_{user}\cdot Em{b}_{item}$或$cosine(Em{b}_{user},Em{b}_{item})$时，才产生用户信息与物料信息的唯一一次交叉

• 通过上述的解耦方式并结合以下的操作，可以实现实时性

1）离线时，提前计算好，生成百万、千万级的物料向量(如$Em{b}_{item}$)，灌入Faiss 并建立好索引
2）在线时，独立生成用户向量(如$Em{b}_{user}$)，在Faiss中利用近似最近邻(ANN)搜索算法快速搜索出与$Em{b}_{user}$接近的$Em{b}_{item}$

2.4、如何定义优化目标

• 在定义损失函数上，精排要求的是预测值的“绝对准确性”，一般使用二分类交叉熵损失；
• 而召回的候选集非常庞大，主要考虑的是排序的相对准确性，因为只有正样本来自用户真实反馈，负样本往往未曾曝光过，所以召回没要求预测值绝对准确
• 召回常用的损失函数：1）多分类的Softmax Loss，只要求正样本的概率值预测得越高越好；2）Learning-To-Rank思想的损失

2.4.1、Softmax Loss、NCE Loss、NEG Loss

• Softmax Loss如下：
  
• NCE Loss中，用$G(u,t)$表示该样本$(u,t)$是正样本的Logit，公式如下：
  $$G(u,t)=u\cdot t-logQ(t|u)$$

Q(t|u)表示来自噪声的概率，可以理解为用户不喜欢但随手点击过的概率。考虑推荐系统的实际情况，我们不难得出“Q(t|u)应该与物料t的热度正相关”的结论。t越热门，它被展示给用户的频率越高，被用户随手点击的概率也就越高。

• 这里的重点在于理解修正项-logQ(t|u)的作用：为了防止热门物料被过度惩罚。可以这样来理解，在负采样的时候，物料的热度越高，它被采样为负样本的概率也就越高。负样本主要由热门物料组成，实际上是对热门物料进行了过度打压，可能会导致推荐结果过于小众。为了补偿被过度打压的热门物料，要求$u\cdot t$不能只是一般大，而必须在减去logQ(t|u)之后依然很大。
• 根据G(u, t)计算BCE Loss，得到NCE Loss(Noise Contrastive Estimation)
  L N C E = − 1 ∣ B ∣ ∑ ( u i , t i ) ∈ B [ log ⁡ ( σ ( G ( u i , t i ) ) ) + ∑ j ∈ S i log ⁡ ( 1 − σ ( G ( u i , t j ) ) ] = 1 ∣ B ∣ ∑ ( u i , t i ) ∈ B [ log ⁡ ( 1 + exp ⁡ ( − G ( u i , t i ) ) ) + ∑ j ∈ S i log ⁡ ( 1 + exp ⁡ ( G ( u i , t j ) ) ) ]
  LNCE=−1|B|∑(ui,ti)∈B[log⁡(σ(G(ui,ti)))+∑j∈Silog⁡(1−σ(G(ui,tj))]=1|B|∑(ui,ti)∈B[log⁡(1+exp⁡(−G(ui,ti)))+∑j∈Silog⁡(1+exp⁡(G(ui,tj)))]" role="presentation" style="position: relative;">LNCE=−1|B|∑(ui,ti)∈B[log(σ(G(ui,ti)))+∑j∈Silog(1−σ(G(ui,tj))]=1|B|∑(ui,ti)∈B[log(1+exp(−G(ui,ti)))+∑j∈Silog(1+exp(G(ui,tj)))]$$\begin{array}{rl}{L}_{\mathrm{N}\mathrm{C}\mathrm{E}}& =\frac{-1}{|B|}\sum _{\left(u_i,t_i\right)\in B}[\log \left(\sigma \left(G\left(u_i,t_i\right)\right)\right)+\sum _{j\in S_i}\log \left(1-\sigma \left(G\left(u_i,t_j\right)\right)\right]\\ & =\frac{1}{|B|}\sum _{\left(u_i,t_i\right)\in B}\left[\log \left(1+\exp \left(-G\left(u_i,t_i\right)\right)\right)+\sum _{j\in S_i}\log \left(1+\exp \left(G\left(u_i,t_j\right)\right)\right)\right]\end{array}$$
  LNCE​​=∣B∣−1​(ui​,ti​)∈B∑​ ​log(σ(G(ui​,ti​)))+j∈Si​∑​log(1−σ(G(ui​,tj​))]=∣B∣1​(ui​,ti​)∈B∑​ ​log(1+exp(−G(ui​,ti​)))+j∈Si​∑​log(1+exp(G(ui​,tj​))) ​​

$S_i$表示随机采样物料作为负样本

• 在实际操作中为了简化计算，可以忽略-logQ(t|u)修正项，得到NEG Loss（Negative Sampling Loss）：
  $$L_{NEG}=\frac{1}{|B|}\sum _{(u_i,t_i)\in B}[log(1+exp(-u_i\cdot t_i))+\sum _{j\in S_i}log(1+exp(u_i\cdot t_i)]$$

2.4.2、Sampled Softmax Loss

• Sampled Softmax Loss中，以概率Q(t|u)采样一批负样本S，类似NCE Loss，可以得到：
  $$G(u,t)=u\cdot t-logQ(t|u)$$
• 与NCE Loss一样，存在修正项，防止热门物料被过度打压。并且修正只发生在训练阶段，预测阶段还是$u\cdot t$
• 把G(u, t)带入Softmax Loss中，得到Sampled Softmax Loss：
  $$L_{SampledSoftmax}=-\frac{1}{|B|}{\sum }_{(u_i,t_i)\in B}log\frac{exp(G(u_i,t_i))}{exp(G(u_i,t_i))+{\sum }_{j\in S_i}exp(G(u_i,t_j))}$$

$S_i$是采样生成的负样本集合

2.4.3、Pairwise Loss

• 是Learning-To-Rank思想的一种实现，以U2I为例：样本为用户、交互过的正向物料、随机采样的负向物料的三元组$(u_i,t_{i+},t_{i-})$
• 对于用户u，与正向物料的匹配程度要远高于负向物料的匹配度，因此使用Marginal Hinge Loss：
  $$L_{Hinge}=\frac{1}{|B|}\sum _{(u_i,t_{i+},t_{i-})}max(0,m-u_i{\cdot }_{i+}+u_i\cdot t_{i-})$$
• m是一个边界值，为超参数

3、Word2Vec：转为Item2Vec

• 参考：https://blog.csdn.net/m0_48086806/article/details/136914225
• 四个维度如下：

定义正样本：Item2Vec也采用滑窗，即只在某个物料前后出现其他物料彼此相似，为正样本

定义负样本：整个物料库随机采样为负样本

如何Embedding：只定义了待学习的Embedding矩阵，每行就是对应物料的Embedding向量

定义损失函数：使用NEG Loss

4、Airbnb召回

• Airbnb针对民宿业务的特点，在Item2Vec基础上，对正负样本的定义进行了修改

定义正样本：额外增加了正样本，即点击序列中的每个房屋与最终成功预定的房屋是相似的

定义负样本：整个物料库随机采样为负样本，采样每个房屋与其同城的其他房屋作为Hard Negative

如何Embedding：只定义了待学习的Embedding矩阵，每行就是对应物料的Embedding向量

定义损失函数：使用NEG Loss，增加了额外的正负样本

5、阿里的EGES召回

• 阿里的Enhanced Graph Embedding with Side Information（EGES），进行了如下改进：

定义正样本：考虑了跨用户、跨Session的相似性，可以提高模型的扩展性，生成的新序列中定义滑窗，窗口内的物料是相似的，为正样本

定义负样本：整个物料库随机采样为负样本

如何Embedding：引入了每个物料的属性信息，定义了1+n个Embedding矩阵，包括1个物料ID的Embedding，和不同属性的Embedding；合并他们可以采用Average Pooling的方式

定义损失函数：使用NEG Loss

6、FM：召回算法

• FM不仅能用于精排，也可以用于召回和粗排
• FM主要应用于U2I召回场景，在此存在一个打压热门物料的问题

在正样本中，希望能够打压热门物料，防止过拟合，即不希望正样本被少数热门物料所垄断，正样本采样概率为：

在负样本中，希望能够热门物料过采样，但也要防止热门物料过度惩罚，因此在NCE Loss中由修正项-logQ(t|u)

7、主力召回：双塔模型

• 双塔模型是最主要的召回算法

7.1、正样本定义

U2I召回：用户与他交互过的物料相互匹配，为一对正样本

I2I召回：一个用户在一个Session中交互过的物料$t_i$和$t_j$，为一对正样本

U2U召回：一个用户的一半历史行为和同一个用户的另一半历史行为，为一对正样本

7.2、简化负采样

• 实践中，一般不从全体候选物料中进行选取，因为候选物料太大而且还在动态更新，采样代价太高，同时对于未曝光的物料，没有现成特征使用
• 因此一般采用Batch内负采样、混合负采样

1）Batch内负采样

• 做法如下：

以U2I为例，在一个Batch内，$(u_i,t_j)$为正样本。$u_i$与除了$t_i$之外的其他正样本的物料组成负样本，即$(u_i,t_j),\forall j\in B-i$

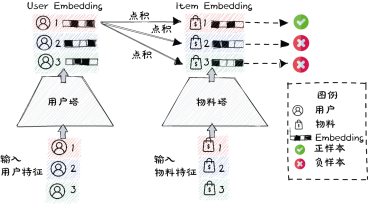
• 缺点是容易造成样本选择偏差。Batct内负采样所采集到的负样本都是Hard Negative(大多数用户都喜欢热门物料)，缺少与用户兴趣毫不相关的 Easy Negative。

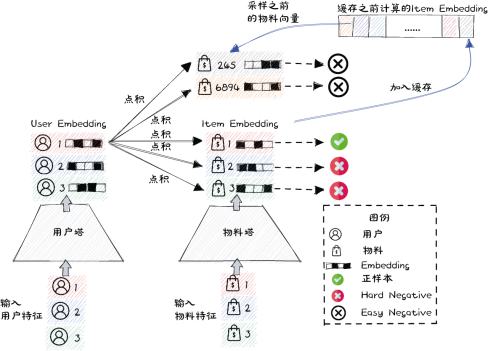
2）混合负采样

• 做法如下：

1）额外建立了一个向量缓存，存储物料塔在训练过程中得到的最新的物料向量。
2）在训练每个 Batch 的时候，先进行 Batch 内负采样，同一个 Batch 内两条样本中的物料互为 Hard Negative.
3）额外从向量缓存采样一些由物料塔计算好的之前的物料向量B’，作为Easy Negative 的Embedding.

• 混合负采样对物料库的覆盖更加全面，更加符合负样本要让召回模型“开眼界、见世面”的一般原则。

7.3、双塔结构

• 结构如下：
  
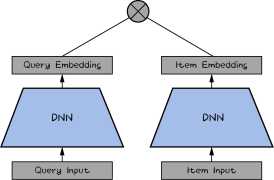
• 对于单塔来说，结构特点如下：

1）用户特征喂入用户塔，输出用户向量；物料(无论正向还是负向)特征喂入物料塔，输出物料向量。

2）塔的底座宽。双塔能够接受的特征很丰富，用户侧可以包括 User D、用户的属性(如性别、年龄)、用户画像(如用户对某个标签的CTR)、用户的各种行为历史(如点击序列)。物料侧可以包括 Item 、物料的基本属性(如店铺、品牌)、物料静态画像(如所属类别)、物料动态画像(如过去1天的 CTR)，还可以包括由内容理解算法生成的各种文字、图像、音频、视频的向量。

3）塔身很高，每层的结构可以很复杂，可以完成充分而复杂的交叉，模型的表达能力相较于之前的 [tem2Vec、FM 召回大为增强。

• 对于双塔来说，双塔模型要求两塔之间绝对独立、解耦。只允许在生成最终的用户向量和物料向量之后才点积交叉一次。

7.4、Sampled Softmax Loss的技巧

• 损失函数如下：
  

1）L2正则化

• 用户向量和物料向量计算点积之前，先除以各自的L2范数，以实现归一化，类似于cosine(u, t)

2）温度调整难度

• $\tau$是温度系数，起一个放大作用：但凡有哪个负样本$(u_i,t_j)$没被训练好，导致点积>0，$\frac{1}{\tau }$就能把这个“错误”放大许多倍，导致分母变大，损失增加。那个没被训练好的负样本就会被模型聚焦，被重点“关照”
• $\tau$调节召回结果的记忆性与扩展性

如果$\tau$设置得很小，它对错误的放大功能就很强，因此错误就很难犯。但是，$\tau$过小的话，将使模型牢牢记住用户历史点击反映出的兴趣爱好，召回时不敢偏离太远。推荐结果的精度高，但对用户潜在兴趣覆盖得不够，容易使用户陷入“信息茧房”而疲劳。

果$\tau$设置大了，对错误的放大功能就弱，可以覆盖一部分潜在兴趣，但也有可能召回精度不够，损害用户体验

3）采样概率修正

• Q(t)是负采样到物料t的概率，而-logQ(t)类似NCE Loss，防止热门物料被过度打压而进行的修正，

参考书籍：
《互联网大厂推荐算法实战》