如果需要了解其他图像处理的文章,请移步小编的GitHub地址
传送门:请点击我
如果点击有误:https://github.com/LeBron-Jian/ComputerVisionPractice
VisionPro有很多的示例和算子,这里再展示一个比较好用的算子FitLine Tool。我自己的笔记不会按照顺序一一展示出来的,也许那个文章先OK,我会先release出来的。 其中大部分的图片和步骤都是VisionPro的官方文档,我这里只是自己的学习笔记,不做任何商用。
在计算机视觉和图像处理领域,直线拟合是一个常见的问题。当我们有一系列的数据点,并希望找到一条最能代表这些数据的直线时,就需要用到直线拟合算法。而VisionPro就有一个非常好用的直线拟合算子FitLineTool。这里我会介绍一下。当然目前已经更新了SmartlineTool,这些后续再说哈。
首先,我会展示一下FitLine这个算子的页面。其次我会根据这个算子的使用步骤学习一下这个算子的原理。这个算子非常好理解,顾名思义就是直线拟合嘛。肯定是根据我们输入的一系列二维坐标点拟合成一条直线,并将直线在终端输出。(注意至少需要两个坐标点才能拟合直线哈)。下面简单过一下。
1,VisionPro 界面文档
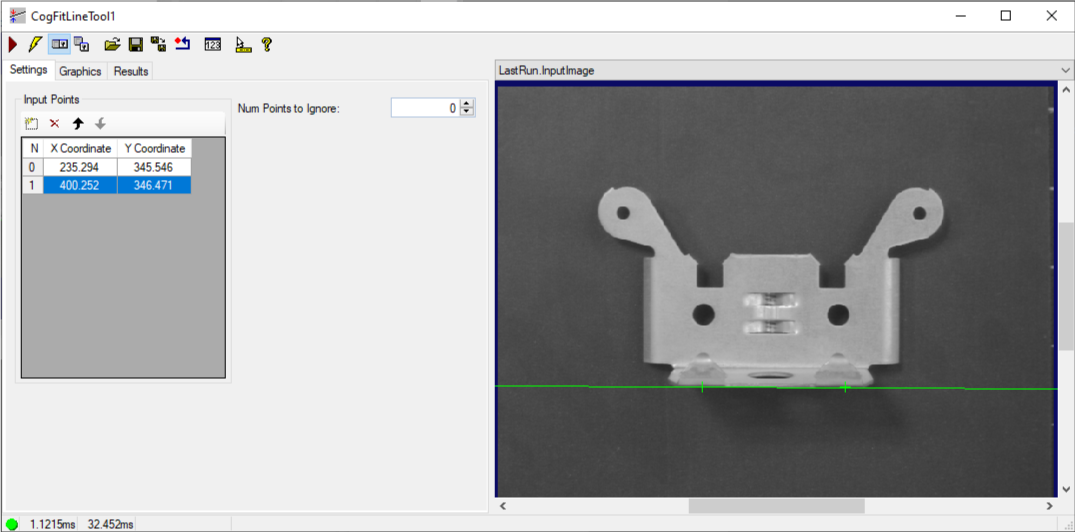
- Current.InputImage 缓冲区包含当前图像和提供给工具的输入点集。
- LastRun.InputImage 缓冲区包含工具在将线拟合到输入点集之后的结果。
1,设置
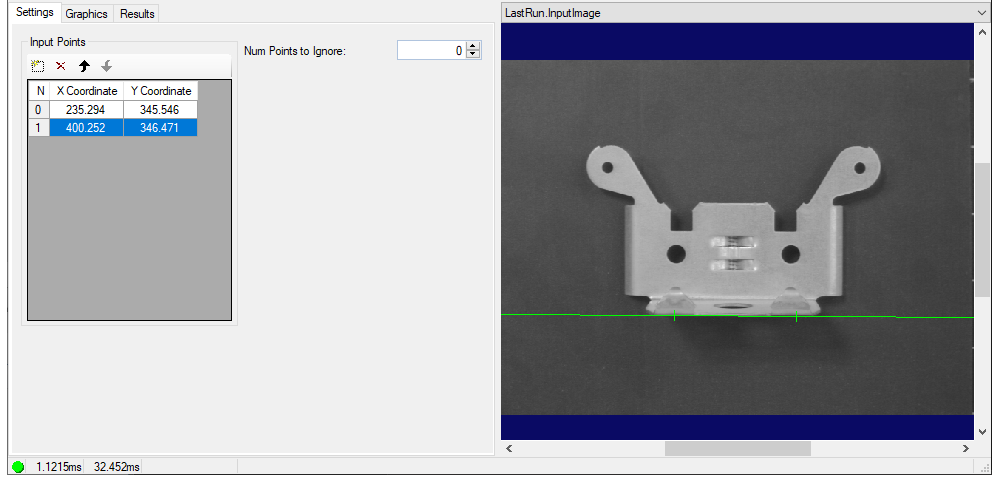
1.1 输入点

默认是最少两个点,如果拟合直线,少于两个点会报错(原因很简单,两点确定一条直线嘛)!!!
下图展示了只输入一个点,FitLineTool的报错情况:

1.2 要忽略的点
2,图形
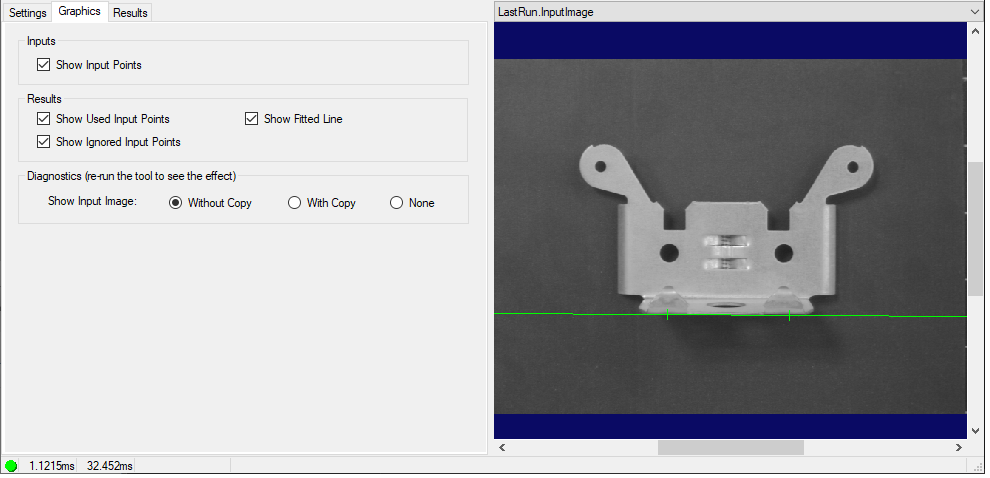
该选项卡提供下列选项:

3,结果
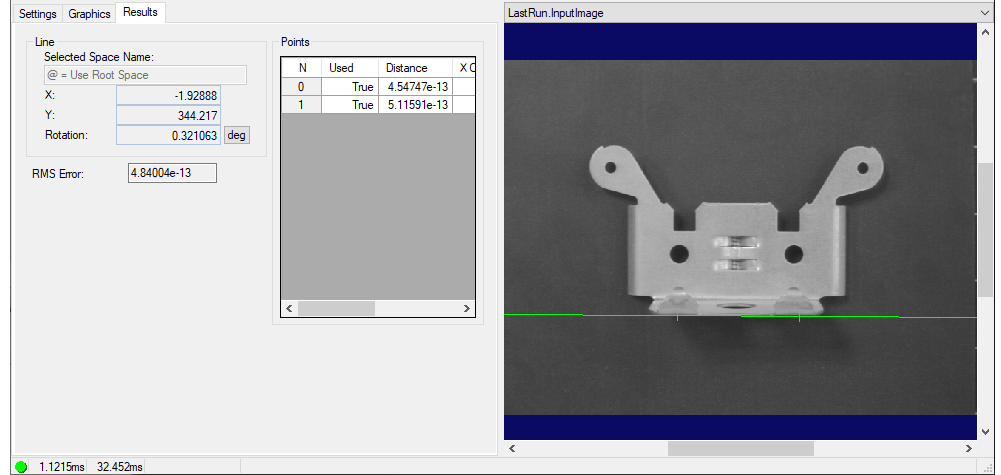

下面三张图是一个结果图,只是输出不能全部一行展开,所以我就截图分开。
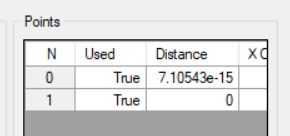

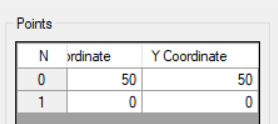
2,拟合线的算法原理介绍
2.1 VisionPro FitLineTool 原理
官网上放的东西,我都一一罗列下来,具体使用了什么,我这里就不再详细分析了,毕竟属于人家商业机密。哈哈哈

你可以指定FitLine 工具忽略所提供的部分点。在丢弃允许工具忽略的点数后,工具会尝试使用您提供的点的每个可能组合来拟合线。此工具会丢弃边远点以使用其余点拟合最佳可能的线。
RMS概念
- 对一组数值进行平方。
- 计算平方值的平均值。
- 取平均值的平方根。

2.2 OpenCV fitline 直线拟合函数
下图是OpenCV官方文档中,对直线拟合函数的详细介绍,这个可以好好分析,毕竟是开源的哈。
FitLine算法是一直基于最小二乘法的直线拟合算法。他的基本思想是通过最小化所有点到直线的距离的平方和来估计直线参数。具体来说,我们先假设一条直线的方程为 y=kx+b, 其中k和b是直线的斜率和截距。然后,根据给定的数据点,我们可以构建一个关于k和b的方程组。通过求解这个方程组,我们可以得到直线的参数。FitLine算法的优点是计算速度快,适用于处理大规模数据集。但是,他对噪声和异常值比较敏感,如果数据集中存在较多的噪声或异常值,拟合出的直线可能会偏离真实直线。
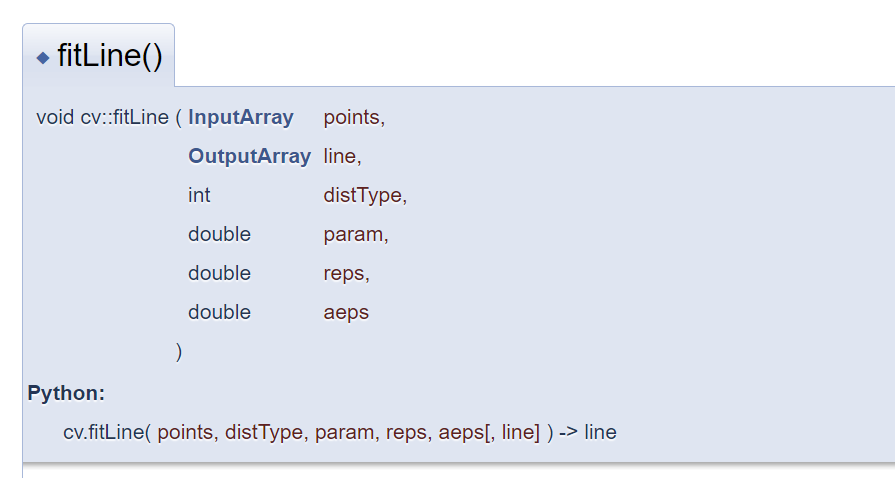
上面很清楚的看到,FitLine函数用于对二维或三维空间中的点集进行直线拟合。共有六个参数(包括输入输出)。
由下可知,CV_DIST_L2为最简单快速的最小二乘法,推荐使用。官方文档中介绍,这里使用的拟合算法是M-estimator方法


具体操作,大家根据自己的实际情况使用。
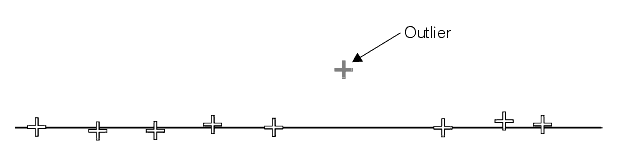
直线拟合的原理很简单,就是给出多个点,然后根据这些点拟合出一条直线,最常见的算法是多约束方程的最小二乘拟合,如下图所示:

但是当这些点当中有一个或者几个离群点(outlier)时候,最小二乘拟合出来的直线就直接翻车了。原因是最小二乘无法在估算拟合的时候剔除或者降低离群点的影响,于是一个聪明的家伙出现了,提出了基于权重的最小二乘拟合估算方法,这样就避免了翻车。根据高斯分布,离群点权重应该尽可能的小,这样就可以降低它的影响,OpenCV中的直线拟合就是就权重最小二乘完成的,在生成权重时候OpenCV支持几种不同的距离计算方法,分别如上面所描述的。其中DIST_L2是最原始的最小二乘,最容易翻车的一种拟合方式,虽然速度快点。所以VisionPro作为商用算子,肯定考虑了这些因素。具体也在其参数列表里面体现了,可以剔除离群因子。
2.3 RANSAC算法
除了上面提到的FitLine算法(基于最小二乘法的直线拟合算法),还有RANSAC算法(随机抽样一致算法),这是一种基于随机抽样的算法。他的基本思想是从数据中随机抽取一定数量的点,然后根据这些点来估计模型参数。接着,用该模型来测试所有的数据点,计算每个点到直线的距离,如果距离小于某个阈值,则认为该点是内点。最后,通过迭代这个过程,找到包含最多内点的模型,即为最佳模型。
RANSAC算法的优点是鲁棒性强,能够处理包含噪声和异常值的数据集。但是,它的计算复杂度较高,需要多次迭代才能找到最佳模型。在实际应用中,我们需要根据具体场景来选择合适的算法。如果数据集包含较多的噪声或异常值,我们可以选择RANSAC算法来提高拟合的鲁棒性;如果数据集规模较大且对计算速度有较高要求,我们可以选择Flitline算法来提高拟合效率。当然,除了这两种算法之外,还有许多其他的直线拟合算法,如霍夫变换、最小中值平方等。在实际应用中,我们可以根据具体需求来选择合适的算法。
RANSAC算法原理
实际上,RANSAC算法的核心在于将点划分为“内点”和“外点”。在一组包含“外点”的数据集中,采用不断迭代的方法,寻找最优参数模型,不符合最优模型的点,被定义为“外点”。这就是RANSAC的核心思想。
其目标:一个模型与含有野值的数据集S的鲁棒拟合。
算法步骤:
- 1,随机地从 S 中选择 s 个数据点组成一个样本作为模型的一个例示
- 2,确定在模型距离阈值 t 内的数据点集 Si, Si称为采样的一致集并定义S的内点
- 3,如果 Si 的大小(内点的数目)大于某个阈值 T ,用 Si 的所有点重估模型并结束
- 4,如果 Si 的大小小于 T, 选择一个新的子集并重复上面的过程
- 5,经过 N 次试验选择最大一致集 Si, 并用 Si 的所有点重估计模型