-
面试经典150题——路径总和

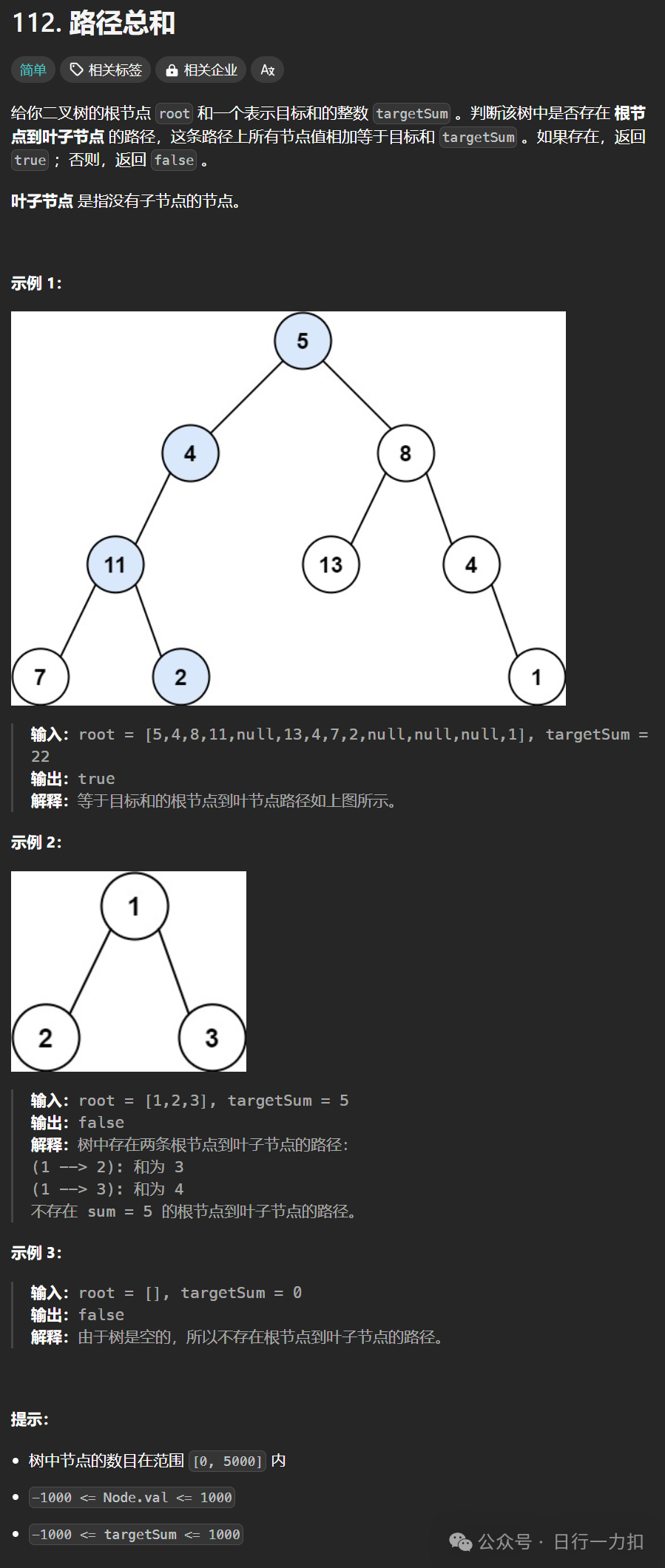
1. 题目描述
2. 题目分析与解析
2.1 思路一
注意题目的关键点:判断该树中是否存在 根节点到叶子节点 的路径,起点是root,终点是叶子节点。
那么我们就可以从根节点按照层序遍历的方式,从根节点从根到 叶子不断对路径进行加和(注意:层序遍历需要使用一个队列存储每一层的节点),就可以按照如下步骤进行:
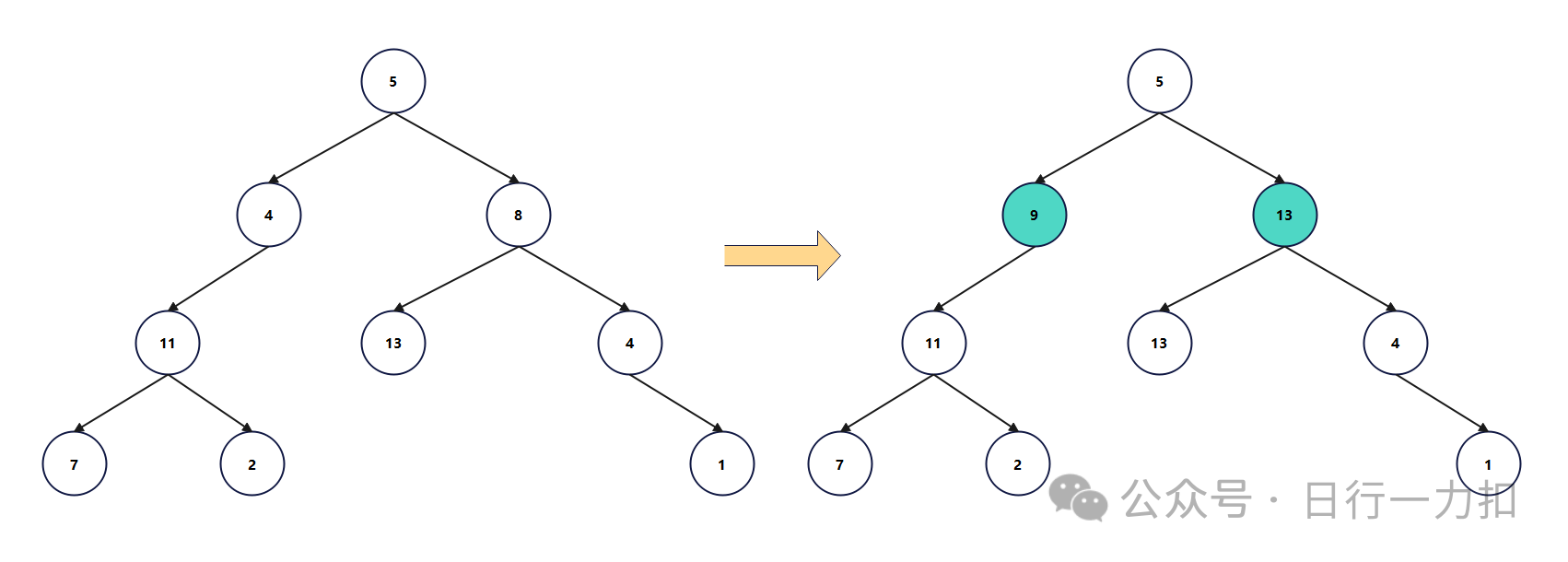
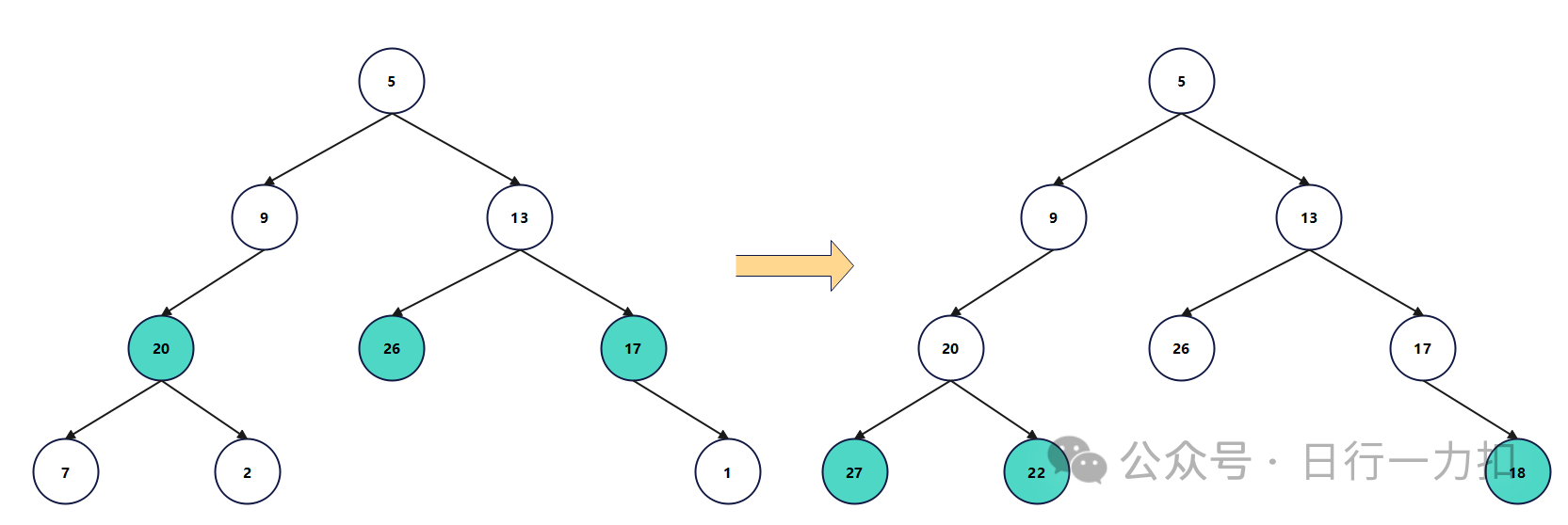
最后发现当前层有叶子节点的值是targetSum就说明返回true,否则返回false。
2.2 思路二
因为我们在思路一按照层序遍历,不可避免地使用了一个存储当前层级的队列,那么能不能不用队列也能实现呢?答案是可以的。
因为我们已经有了targetSum,并且我们在从根节点向下遍历的过程中,如果要实现从root到某一个叶子节点的路经总和为targetSum,那么我们是不是也就相当于我从根节点root走到下一个节点root.left或者root.right,剩下的路径距离
targetSum - root.val?也就是按照先序遍历的方式,每走过一段路就用targetSum - 当前节点的.val最后到达叶子节点判断是否剩余路径等于此时的targetSum就可以了。3. 代码实现
3.1 思路一
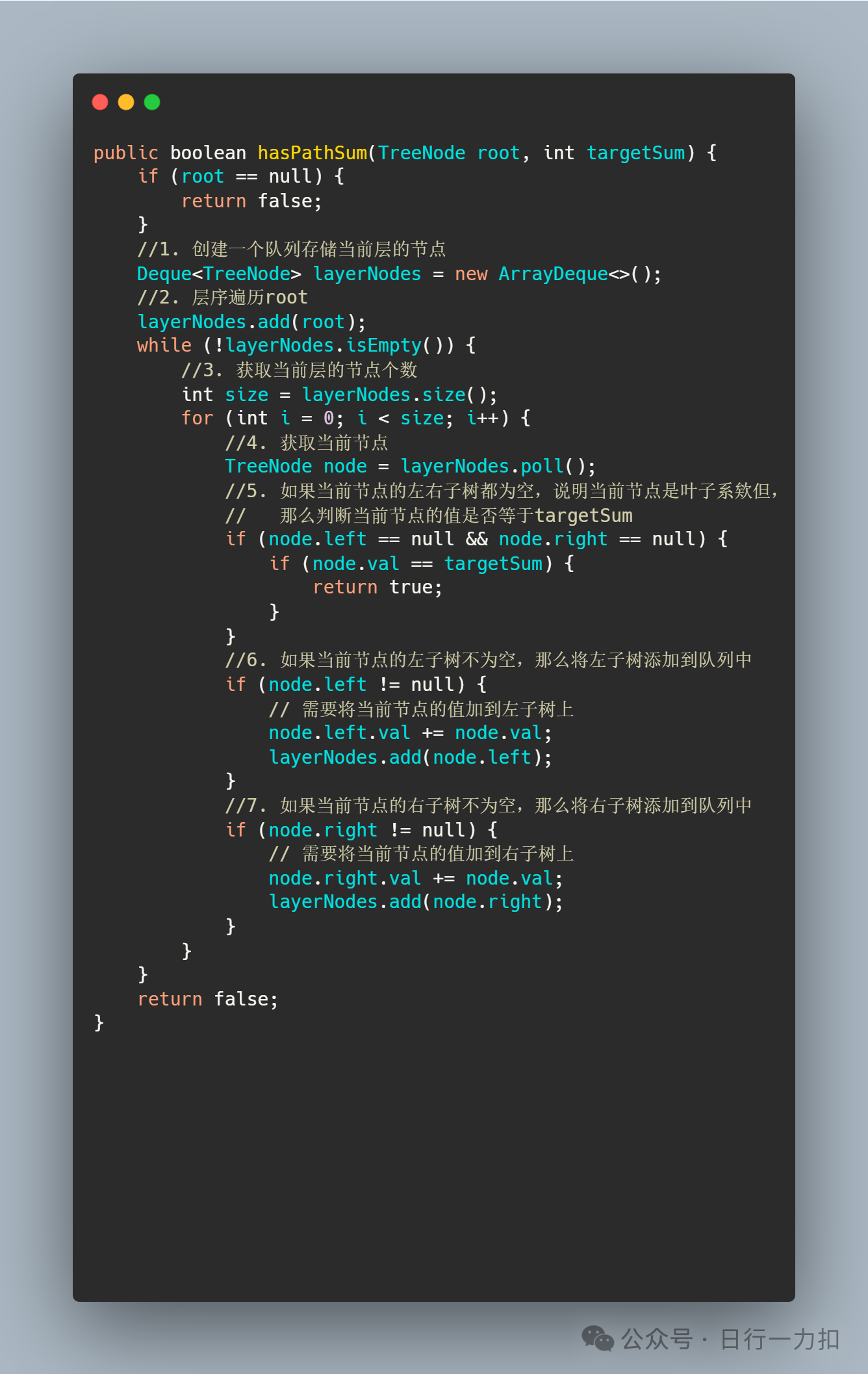
3.2 思路二
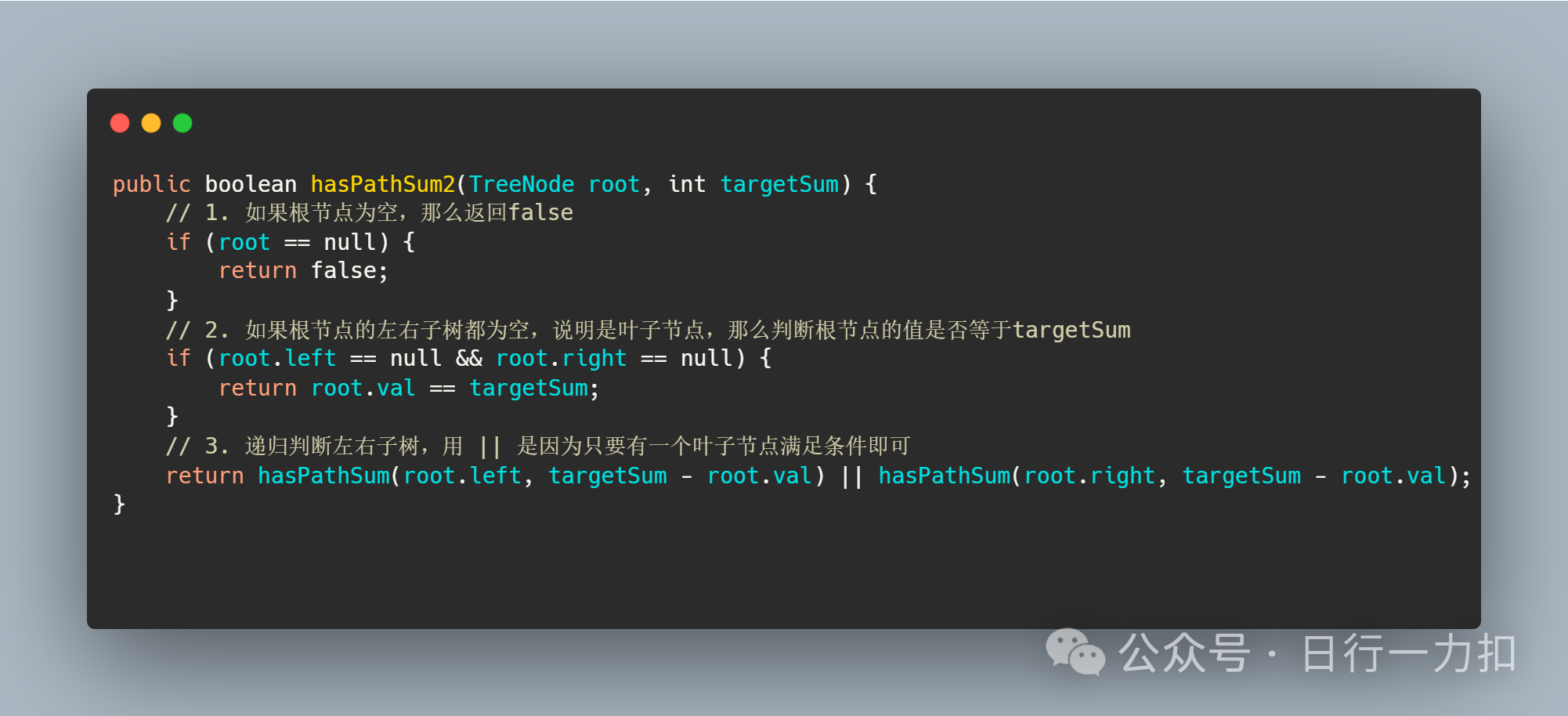
4. 相关复杂度分析
4.1 方法
hasPathSum(BFS 使用队列)时间复杂度
-
最坏情况: 在最坏的情况下,需要遍历树中的每一个节点。因此,时间复杂度为 (O(N)),其中 (N) 是树中节点的数量。
-
最佳情况: 如果你在树的较浅层就找到了符合条件的路径,你可能不需要遍历所有节点。但理论上,这依然保持 (O(N)),因为在最坏情况下你需要遍历所有节点。
空间复杂度
-
空间复杂度: 由于使用了队列来存储每一层的节点,空间复杂度主要取决于树的宽度(即最宽的那层有多少个节点)。在最坏的情况下(完全二叉树),最底层大约包含 (N/2) 个节点,因此空间复杂度也是 (O(N))。
2. 方法
hasPathSum2(DFS 使用递归)时间复杂度
-
时间复杂度: 与 BFS 方法类似,DFS 方法在最坏情况下也需遍历树的每一个节点来确认是否存在符合条件的路径,因此时间复杂度也是 (O(N))。
空间复杂度
-
空间复杂度: 递归方法的空间复杂度主要由递归调用栈的深度决定,这取决于树的高度。在最坏情况下(树完全不平衡,如退化成链表),空间复杂度为 (O(N))。在最好的情况下(树完全平衡),空间复杂度为 (O(\log N))。
总结来说,两种方法在时间复杂度上都是 (O(N)),而在空间复杂度上,DFS在最好情况下优于BFS,因为平衡树的高度远小于节点数。BFS由于需要存储至少一整层的节点,所以在空间上可能消耗更多,特别是在树的层次较多时。
-
-
相关阅读:
docker 安装mysql
【视觉预训练】《BEIT: BERT Pre-Training of Image Transformers》 ICLR 2022
「深入探究Web页面生命周期:DOMContentLoaded、load、beforeunload和unload事件」
Kubernetes---使用端口转发来访问集群中的应用
【排序24:俄罗斯套娃信封问题】(动态规划 / 二维最长公共子序列 / 基于二分查找的动态规划)
tomcat下载安装及配置教程
深入理解New操作符
【Java】JDK11特性概览
计算机网络408考研 2020
计算机网络常见面试题
- 原文地址:https://blog.csdn.net/m0_60388871/article/details/138153149