直接插入排序与希尔排序的详解及对比

目录

1.直接插入排序（至少有两个元素才可以使用）

        排序逻辑

B站动画演示：直接插入排序

逻辑转为代码：

稳定性：稳定

时间复杂度：O(N^2)

空间复杂度：O(1)

应用场景

2.希尔排序（对直接插入排序的优化）

希尔排序（也叫缩小增量排序）定义

预排序

逻辑转为代码

时间复杂度

稳定性：不稳定

---

1.直接插入排序（至少有两个元素才可以使用）

        排序逻辑

排序方式其实就是从第一个元素开始插入，把接下来要插入的元素放在当前集合的合适的位置。

有点云里雾里，没事看下面例子，我来演示一遍。

对arr{8 5 7 2 1 4 3}排升序为例（排降序逻辑是一样的，只是比较方式，恰好相反）：

事前，需要定义三个变量：

1.两个int类型的下标指向两个元素，分别是：

               endIndex(在最开始，指向数组第二个元素，也就是5)

               con（在最开始，指向数组首元素）

注意：排序过程中，小标区间[0,con]所指向的元素集合永远都是有序的

2.一个int类型的变量tmp，用来存“挖出来的”元素

---

前2个元素排序：

因为5已经被tmp存起来了，所以可以假想5这个元素，被挖了出来（当然此时他还存在与数组）：

        

三个变量都起到了应有的功能，可以开始排序了：

        如果tmp<arr[con]，那么arr[con+1]=arr[cont]

         然后con++

如图：

此时con==-1了，说明“前两个元素已经排好了”

只需要把tmp的值给到arr[con+1]即可。

如图：

好了，可以更新endIndex/tmp/con，然后进行前3个元素排序

con=endIndex

endIndex++

tmp=arr[endIndex]

如图：

快看！直接插入排序会保证区间[0,con]一定有序！

---

前3个元素排序：

在上图中，如果tmp

则执行同样的操作：

arr[con+1]=tmp

con--

如图

此时，出现了新的情况

tmp不在小于arr[con]了

说明“前3个元素排序已经完成”

arr[con+1](元素本来是8)=tmp(赋值成7)

如图：

然后就可以调整endIndex/tmp/con，进行前4个元素排序：

快看！直接插入排序会保证区间[0,con]一定有序！

一下的排序直接用图演示，逻辑和前面一样：

前4个元素排序：

让arr[con+1]=tmp，然后进行前5个元素排序:

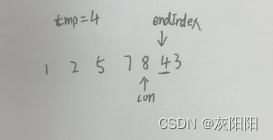
进行前6个元素排序：

此时tmp>arr[con]，说明，"已经排序好了"，直接赋值arr[con+1]=tmp:

如上图，最后一次排序你来试试？

B站动画演示：直接插入排序

逻辑转为代码：

class InsertSort {
 
    public void insert(int[] arr) {
        if (arr.length == 1) return;//只有一个元素，可以直接返回，因为一个数字，就是有序的
        int tmp = 0;//用来存放endIndex所指向的元素
        for (int endIndex = 1; endIndex < arr.length; endIndex++) {
            tmp = arr[endIndex];
            int con = endIndex - 1;
            for (; con >= 0; con--) {
                if (tmp < arr[con]) {
                    arr[con + 1] = arr[con];
                }else{//如果tmp>=arr[con]说明已经排序完成（区间[0,con]），只要arr[con+1]=tmp即可
                    break;
                }
            }
            arr[con + 1] = tmp;
        }
    }
}

稳定性：稳定

时间复杂度：O(N^2)

在最坏的情况，就是

需要排升序，但是所给的数组刚好是降序，反之亦然。

此时，从第二个元素开始排序，那么时间复杂度就===

1+2+3+.......+N-1（排列N-1次，每次都要走完已经排列好的数组）

简化一下==

1+2+3+4....+N=N(1+N)/2=（N+N^2）/2=O(N^2)

空间复杂度：O(1)

没什么好说的

应用场景

根据直接插入排序的排序特点，如果一个序列越接近有序，那么直接插入排序的时间复杂度就越小。

所以：

当前有一组数据 基本上趋于有序 那么就可以使用直接插入排序

2.希尔排序（对直接插入排序的优化）

如标题所讲，希尔排序与直接插入排序有千丝万缕的关系。

事实也的确如此。

我们在前直接插入排序的应用场景一节讲过：直接插入排序在接近有序时，时间会快很多。

所以，有一个叫希尔（Shell）的大神就想到了这样一个办法：

        先对数组进行预排序了，然后在使用直接插入排序，时间不就得到了优化吗？

希尔排序（也叫缩小增量排序）定义

先选定一个整数，把待排序文件中所有记录分成多个组， 所有距离为的记录分在同一组内，并对每一组内的记录进行排序。然后，取，重复上述分组和排序的工作。当到达 =1时，所有记录在同一组内排好序。

预排序

其实就是定义里所说的分成多个组，对每一个组中的元素进行排序即可。

如图：

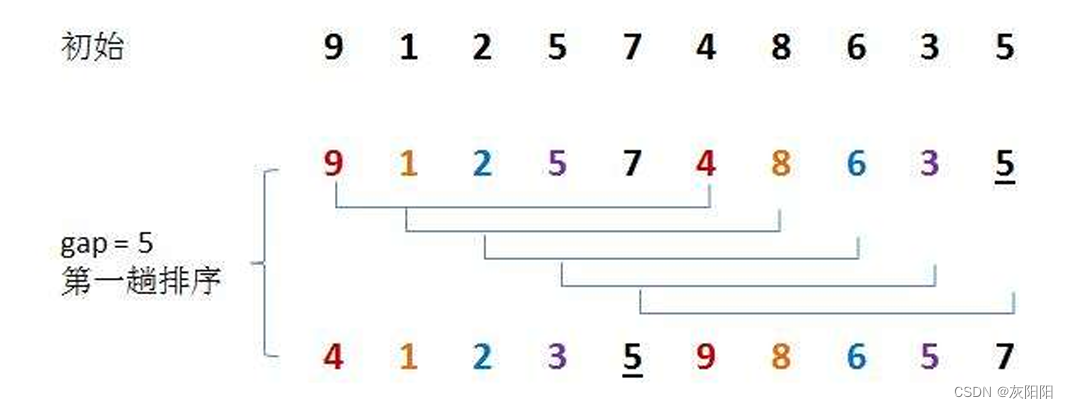
gap/=2----直到gap为1（就是纯的直接插入排序了）

观察一下，上面的数组是不是非常接近有序了？

此时gap/=2就是1，也就是对整个数组进行直接插入排序，那么排序速度就可以变得很快了。

逻辑转为代码

class Shell {
 
    public void shellSort(int[] arr) {
        int gap = arr.length-1;//这里gap初始值，直接给到整个数组的长度
        while (gap > 0) {
            shell(arr, gap);
            gap /= 2;//每次减少一半的间隔
        }
    }
 
    private void shell(int[] arr, int gap) {//此方法，就十分类似直接插入排序了，基本就是把1换成gap
        for (int i = gap; i < arr.length; i+=gap) {
            int tmp = arr[i];
            int j = i - gap;
            for (; j >= 0; j -= gap) {//往数组前面比较
                if (tmp < arr[j]) {//交换，然后继续往前面比较
                    arr[j + gap] = arr[j];
                }else{
                    //当前这一组数”已经有序了“
                    break;
                }
            }
            arr[j + gap] = tmp;//把坑填上
        }
    }
}

时间复杂度

希尔排序的时间复杂度不好计算，因为gap的取值方法很多，导致很难去计算，因此在好些树中给出的希尔排 序的时间复杂度都不固定(下面图片有兴趣可以看)：

《数据结构-用面向对象方法与C++描述》--- 殷人昆

讲了那么多我们来提炼一下：

希尔排序时间复杂度不好算，这里的gap不好取，涉及到当今没有解决的数学难题，但是大概范围可以给到：

O(N^(1.25))到O(1.6*N^1.25)

稳定性：不稳定