-
【C 数据结构】二叉树
【 1. 基本原理 】
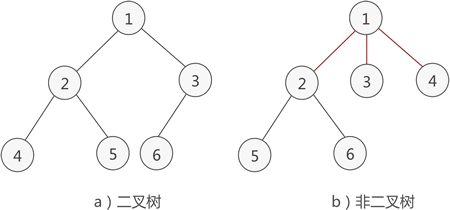
- 满足以下两个条件的树就是 二叉树:
本身是有序树;
树中包含的各个节点的度不能超过 2,即只能是 0、1 或者 2;
例如,图 1a) 就是一棵二叉树,而图 1b) 则不是。
1.1 二叉树的性质
- 二叉树中,第 i 层最多有 2 i − 1 2^{i-1} 2i−1 个结点。
- 如果二叉树的深度为 K,那么此二叉树最多有 2 K − 1 2^K-1 2K−1 个结点。
- 二叉树中,终端结点数(叶子结点数)为 n 0 n_0 n0,度为 2 的结点数为 n 2 n_2 n2,则 n 0 = n 2 + 1 n_0=n_2+1 n0=n2+1 。
性质 3 的计算方法为:对于一个二叉树来说,除了度为 0 的叶子结点和度为 2 的结点,剩下的就是度为 1 的结点(设为 n 1 n_1 n1),那么总结点 n = n 0 + n 1 + n 2 n=n_0+n_1+n_2 n=n0+n1+n2。
同时,对于每一个结点来说都是由其父结点分支表示的,假设树中分枝数为 B,那么总结点数 n = B + 1 n=B+1 n=B+1。而分枝数是可以通过 n1 和 n2 表示的,即 B = n 1 + 2 ∗ n 2 B=n_1+2*n_2 B=n1+2∗n2。所以,n 用另外一种方式表示为 n = n 1 + 2 ∗ n 2 + 1 n=n_1+2*n_2+1 n=n1+2∗n2+1。
两种方式得到的 n 值组成一个方程组,就可以得出 n 0 = n 2 + 1 n_0=n_2+1 n0=n2+1。1.2 满二叉树
- 如果二叉树中除了叶子结点, 每个结点的度都为 2,则此二叉树称为 满二叉树 。如下图所示:
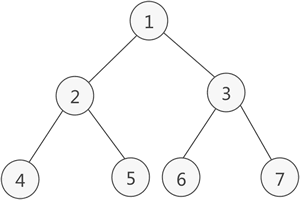
- 满二叉树除了满足普通二叉树的性质,还具有以下性质:
- 满二叉树中第 i 层的节点数为 2 n − 1 2^{n-1} 2n−1 个。
- 深度为 k 的满二叉树必有 2 k − 1 2^{k-1} 2k−1 个节点 ,叶子数为 2 k − 1 2^k-1 2k−1。
- 满二叉树中不存在度为 1 的节点,每一个分支点中都两棵深度相同的子树,且叶子节点都在最底层。
- 具有 n 个节点的满二叉树的深度为 l o g 2 ( n + 1 ) log_2(n+1) log2(n+1)。
1.3 完全二叉树
- 如果二叉树中 除去最后一层节点为满二叉树,而且最后一层的结点依次从左到右分布,则此二叉树被称为 完全二叉树。
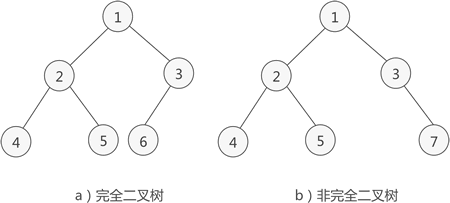
- 满二叉树也是完全二叉树。
- 完全二叉树除了具有普通二叉树的性质,它自身也具有一些独特的性质,比如说,n 个结点的完全二叉树的深度为 [ l o g 2 n ] + 1 [log_2n]+1 [log2n]+1, [ l o g 2 n ] [log_2n] [log2n] 表示取小于 l o g 2 n log_2n log2n 的最大整数。
- 对于任意一个完全二叉树来说,如果将含有的结点按照层次从左到右依次标号,例如上图的完全二叉树。对于任意一个结点 i ,完全二叉树还有以下几个结论成立:
- 当 i>1 时,父亲结点为结点 [i/2] 。(i=1 时,表示的是根结点,无父亲结点)
- 如果 2 × i 2\times i 2×i>n(总结点的个数) ,则结点 i 肯定没有左孩子(为叶子结点);否则其左孩子是结点 2 × i 2\times i 2×i。
- 如果 2 × i 2\times i 2×i+1>n ,则结点 i 肯定没有右孩子;否则右孩子是结点 2 × i 2\times i 2×i+1 。
【 2. 二叉树的顺序存储结构 】
- 二叉树的存储结构有两种,分别为顺序存储和链式存储。
- 二叉树的顺序存储,指的是 使用顺序表(数组)存储二叉树。需要注意的是, 顺序存储只适用于完全二叉树。(满二叉树也可以使用顺序存储,因为满二叉树也是完全二叉树)
- 完全二叉树的转化
如果我们想顺序存储普通二叉树,需要提前将普通二叉树转化为完全二叉树。普通二叉树转完全二叉树的方法很简单,只需给二叉树额外添加一些节点,将其"拼凑"成完全二叉树即可。如下图所示:左侧是普通二叉树,右侧是转化后的完全(满)二叉树。
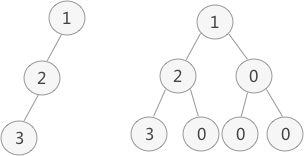
2.1 完全二叉树的顺序存储
- 完全二叉树的顺序存储,仅需从根节点开始,按照层次依次将树中节点存储到数组即可。例如,存储下图中左图所示的完全二叉树,其存储状态如下图中右图所示:
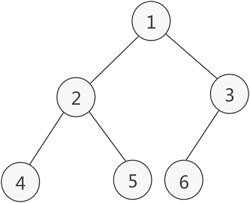

2.2 普通二叉树的顺序存储
- 存储由普通二叉树转化来的完全二叉树也是如此。例如,普通二叉树的数组存储状态如下图中右图所示:
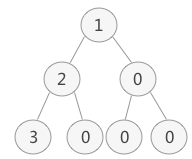

2.3 完全二叉树的还原
- 从顺序表中还原完全二叉树也很简单。完全二叉树具有这样的性质:将树中节点按照层次并从左到右依次标号(1,2,3,…),若节点 i 有左右孩子,则其左孩子节点为 2i,右孩子节点为 2i+1,此性质可用于还原数组中存储的完全二叉树。
【 3. 二叉树的链式存储结构 】
- 其实二叉树并不适合用数组存储,因为并不是每个二叉树都是完全二叉树,普通二叉树使用顺序表存储或多或多会存在空间浪费的现象。
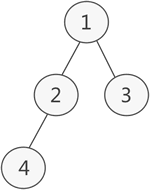
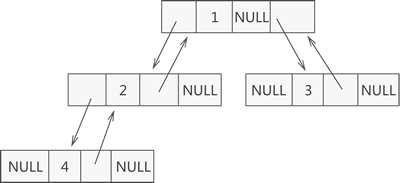
- 如上图所示,此为一棵普通的二叉树,若将其采用链式存储,则只需从树的根节点开始,将各个节点及其左右孩子使用链表存储即可。因此,上图对应的链式存储结构如下图所示:
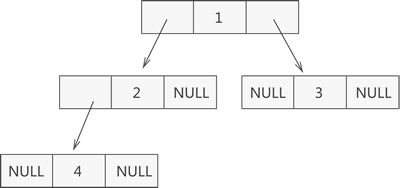
- 由上图可知,采用链式存储二叉树时,其节点结构由 3 部分构成(如下图所示):
- 指向左孩子节点的指针(Lchild);
- 节点存储的数据(data);
- 指向右孩子节点的指针(Rchild);

- 表示该节点结构的 C 语言代码为:
typedef struct BiTNode{ DataType mydata;//数据域 struct BiTNode *lchild,*rchild;//左右孩子指针 struct BiTNode *parent; // 父亲指针(可选) }BiTNode,*BiTree;- 1
- 2
- 3
- 4
- 5
- C实现
#include#include #define TElemType int typedef struct BiTNode{ TElemType data;//数据域 struct BiTNode *lchild,*rchild;//左右孩子指针 }BiTNode,*BiTree; void CreateBiTree(BiTree *T){ *T=(BiTNode*)malloc(sizeof(BiTNode)); (*T)->data=1; (*T)->lchild=(BiTNode*)malloc(sizeof(BiTNode)); (*T)->lchild->data=2; (*T)->rchild=(BiTNode*)malloc(sizeof(BiTNode)); (*T)->rchild->data=3; (*T)->rchild->lchild=NULL; (*T)->rchild->rchild=NULL; (*T)->lchild->lchild=(BiTNode*)malloc(sizeof(BiTNode)); (*T)->lchild->lchild->data=4; (*T)->lchild->rchild=NULL; (*T)->lchild->lchild->lchild=NULL; (*T)->lchild->lchild->rchild=NULL; } int main() { BiTree Tree; CreateBiTree(&Tree); printf("%d",Tree->lchild->lchild->data); return 0; } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 在某些实际场景中,可能会做 “查找某节点的父节点” 的操作,这时可以在节点结构中再添加一个指针域,用于各个节点指向其父亲节点,这样的链表结构,通常称为 三叉链表。如下图所示:
【 4. 二叉树的先序遍历 】
- 二叉树先序遍历的实现思想是:
1.访问根节点;
2.访问当前节点的左子树;
3.若当前节点无左子树,则访问当前节点的右子树;否则重复步骤2。 - 例如下图中二叉树采用先序遍历得到的序列为:1 2 4 5 3 6 7
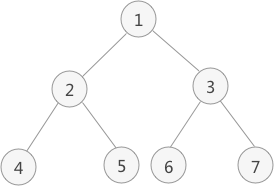
- 以上图为例,采用先序遍历的思想遍历该二叉树的过程为:
访问该二叉树的根节点,找到 1;
访问节点 1 的左子树,找到节点 2;
访问节点 2 的左子树,找到节点 4;
由于访问节点 4 的左子树失败(因为节点4没有左子树),且其也没有右子树,因此以节点 4 为根节点的子树遍历完成。但节点 2 还没有遍历其右子树,因此现在开始遍历,即访问节点 5;
由于节点 5 无左右子树,因此节点 5 遍历完成,并且由此以节点 2 为根节点的子树也遍历完成。现在回到节点 1 ,并开始遍历该节点的右子树,即访问节点 3;
访问节点 3 左子树,找到节点 6;
由于节点 6 无左右子树,因此节点 6 遍历完成,回到节点 3 并遍历其右子树,找到节点 7;
节点 7 无左右子树,因此以节点 3 为根节点的子树遍历完成,同时回归节点 1。由于节点 1 的左右子树全部遍历完成,因此整个二叉树遍历完成;
4.1 递归实现
- 二叉树的先序遍历采用的是递归的思想,因此可以递归实现,其 C 实现为:
#include#include #include //构造结点的结构体 typedef struct BiTNode { int data; //数据域 struct BiTNode* lchild, * rchild;//左右孩子指针 }BiTNode, * BiTree; //模拟操作结点元素的函数,输出结点本身的数值 void displayElem(BiTNode* elem) { printf("%d ", elem->data); } //先序遍历 void PreOrderTraverse(BiTree T) { if (T) { displayElem(T);//调用操作结点数据的函数方法 PreOrderTraverse(T->lchild);//访问该结点的左孩子 PreOrderTraverse(T->rchild);//访问该结点的右孩子 } //如果结点为空,返回上一层 return; } void CreateBiTree(BiTree* T); int main() { BiTree Tree; CreateBiTree(&Tree); printf("先序遍历: \n"); PreOrderTraverse(Tree); } //初始化树的函数 void CreateBiTree(BiTree* T) { *T = (BiTNode*)malloc(sizeof(BiTNode)); (*T)->data = 1; (*T)->lchild = (BiTNode*)malloc(sizeof(BiTNode)); (*T)->rchild = (BiTNode*)malloc(sizeof(BiTNode)); (*T)->lchild->data = 2; (*T)->lchild->lchild = (BiTNode*)malloc(sizeof(BiTNode)); (*T)->lchild->rchild = (BiTNode*)malloc(sizeof(BiTNode)); (*T)->lchild->rchild->data = 5; (*T)->lchild->rchild->lchild = NULL; (*T)->lchild->rchild->rchild = NULL; (*T)->rchild->data = 3; (*T)->rchild->lchild = (BiTNode*)malloc(sizeof(BiTNode)); (*T)->rchild->lchild->data = 6; (*T)->rchild->lchild->lchild = NULL; (*T)->rchild->lchild->rchild = NULL; (*T)->rchild->rchild = (BiTNode*)malloc(sizeof(BiTNode)); (*T)->rchild->rchild->data = 7; (*T)->rchild->rchild->lchild = NULL; (*T)->rchild->rchild->rchild = NULL; (*T)->lchild->lchild->data = 4; (*T)->lchild->lchild->lchild = NULL; (*T)->lchild->lchild->rchild = NULL; } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
4.2 非递归实现
- 递归的底层实现依靠的是栈存储结构,因此,二叉树的先序遍历既可以直接采用递归思想实现,也可以使用栈的存储结构模拟递归的思想实现,其 C 实现为:
#include#include #include int top = -1;//top变量时刻表示栈顶元素所在位置 //构造结点的结构体 typedef struct BiTNode { int data;//数据域 struct BiTNode* lchild, * rchild;//左右孩子指针 }BiTNode, * BiTree; //前序遍历使用的进栈函数 void push(BiTNode** a, BiTNode* elem) { a[++top] = elem; } //弹栈函数 void pop() { if (top == -1) { return; } top--; } //模拟操作结点元素的函数,输出结点本身的数值 void displayElem(BiTNode* elem) { printf("%d ", elem->data); } //拿到栈顶元素 BiTNode* getTop(BiTNode** a) { return a[top]; } //先序遍历非递归算法 void PreOrderTraverse(BiTree Tree) { BiTNode* a[20];//定义一个顺序栈 BiTNode* p;//临时指针 push(a, Tree);//根结点进栈 while (top != -1) { p = getTop(a);//取栈顶元素 pop();//弹栈 while (p) { displayElem(p);//调用结点的操作函数 //如果该结点有右孩子,右孩子进栈 if (p->rchild) { push(a, p->rchild); } p = p->lchild;//一直指向根结点最后一个左孩子 } } } void CreateBiTree(BiTree* T); int main() { BiTree Tree; CreateBiTree(&Tree); printf("先序遍历: \n"); PreOrderTraverse(Tree); } //初始化树的函数 void CreateBiTree(BiTree* T) { *T = (BiTNode*)malloc(sizeof(BiTNode)); (*T)->data = 1; (*T)->lchild = (BiTNode*)malloc(sizeof(BiTNode)); (*T)->rchild = (BiTNode*)malloc(sizeof(BiTNode)); (*T)->lchild->data = 2; (*T)->lchild->lchild = (BiTNode*)malloc(sizeof(BiTNode)); (*T)->lchild->rchild = (BiTNode*)malloc(sizeof(BiTNode)); (*T)->lchild->rchild->data = 5; (*T)->lchild->rchild->lchild = NULL; (*T)->lchild->rchild->rchild = NULL; (*T)->rchild->data = 3; (*T)->rchild->lchild = (BiTNode*)malloc(sizeof(BiTNode)); (*T)->rchild->lchild->data = 6; (*T)->rchild->lchild->lchild = NULL; (*T)->rchild->lchild->rchild = NULL; (*T)->rchild->rchild = (BiTNode*)malloc(sizeof(BiTNode)); (*T)->rchild->rchild->data = 7; (*T)->rchild->rchild->lchild = NULL; (*T)->rchild->rchild->rchild = NULL; (*T)->lchild->lchild->data = 4; (*T)->lchild->lchild->lchild = NULL; (*T)->lchild->lchild->rchild = NULL; } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
【 5. 二叉树的中序遍历 】
- 二叉树中序遍历的实现思想是:
1.访问当前节点的左子树;
2.访问根节点;
3.访问当前节点的右子树;
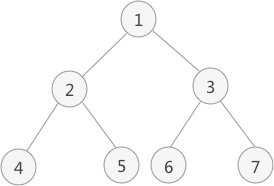
- 上图中二叉树采用中序遍历得到的序列为:4 2 5 1 6 3 7
- 以上图为例,采用中序遍历的思想遍历该二叉树的过程为:
访问该二叉树的根节点,找到 1;
遍历节点 1 的左子树,找到节点 2;
遍历节点 2 的左子树,找到节点 4;
由于节点 4 无左孩子,因此找到节点 4,并遍历节点 4 的右子树;
由于节点 4 无右子树,因此节点 2 的左子树遍历完成,访问节点 2;
遍历节点 2 的右子树,找到节点 5;
由于节点 5 无左子树,因此访问节点 5 ,又因为节点 5 没有右子树,因此节点 1 的左子树遍历完成,访问节点 1 ,并遍历节点 1 的右子树,找到节点 3;
遍历节点 3 的左子树,找到节点 6;
由于节点 6 无左子树,因此访问节点 6,又因为该节点无右子树,因此节点 3 的左子树遍历完成,开始访问节点 3 ,并遍历节点 3 的右子树,找到节点 7;
由于节点 7 无左子树,因此访问节点 7,又因为该节点无右子树,因此节点 1 的右子树遍历完成,即整棵树遍历完成;
5.1 递归实现
- 二叉树的中序遍历采用的是递归的思想,因此可以递归实现,其 C 实现为:
#include#include #include //构造结点的结构体 typedef struct BiTNode { int data;//数据域 struct BiTNode* lchild, * rchild;//左右孩子指针 }BiTNode, * BiTree; //模拟操作结点元素的函数,输出结点本身的数值 void displayElem(BiTNode* elem) { printf("%d ", elem->data); } //中序遍历 void INOrderTraverse(BiTree T) { if (T) { INOrderTraverse(T->lchild);//遍历左孩子 displayElem(T);//调用操作结点数据的函数方法 INOrderTraverse(T->rchild);//遍历右孩子 } //如果结点为空,返回上一层 return; } void CreateBiTree(BiTree* T); int main() { BiTree Tree; CreateBiTree(&Tree); printf("中序遍历算法: \n"); INOrderTraverse(Tree); } //初始化树的函数 void CreateBiTree(BiTree* T) { *T = (BiTNode*)malloc(sizeof(BiTNode)); (*T)->data = 1; (*T)->lchild = (BiTNode*)malloc(sizeof(BiTNode)); (*T)->rchild = (BiTNode*)malloc(sizeof(BiTNode)); (*T)->lchild->data = 2; (*T)->lchild->lchild = (BiTNode*)malloc(sizeof(BiTNode)); (*T)->lchild->rchild = (BiTNode*)malloc(sizeof(BiTNode)); (*T)->lchild->rchild->data = 5; (*T)->lchild->rchild->lchild = NULL; (*T)->lchild->rchild->rchild = NULL; (*T)->rchild->data = 3; (*T)->rchild->lchild = (BiTNode*)malloc(sizeof(BiTNode)); (*T)->rchild->lchild->data = 6; (*T)->rchild->lchild->lchild = NULL; (*T)->rchild->lchild->rchild = NULL; (*T)->rchild->rchild = (BiTNode*)malloc(sizeof(BiTNode)); (*T)->rchild->rchild->data = 7; (*T)->rchild->rchild->lchild = NULL; (*T)->rchild->rchild->rchild = NULL; (*T)->lchild->lchild->data = 4; (*T)->lchild->lchild->lchild = NULL; (*T)->lchild->lchild->rchild = NULL; } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
5.2 非递归实现
- 递归的底层实现依靠的是栈存储结构,因此,二叉树的先序遍历既可以直接采用递归思想实现,也可以使用栈的存储结构模拟递归的思想实现。
- 中序遍历的非递归方式实现思想是:从根结点开始,遍历左孩子同时压栈,当遍历结束,说明当前遍历的结点没有左孩子,从栈中取出来调用操作函数,然后访问该结点的右孩子,继续以上重复性的操作。
- 除此之外,还有另一种实现思想:中序遍历过程中,只需将每个结点的左子树压栈即可,右子树不需要压栈。当结点的左子树遍历完成后,只需要以栈顶结点的右孩子为根结点,继续循环遍历即可。
- C 实现:
#include#include #define TElemType int int top=-1;//top变量时刻表示栈顶元素所在位置 //构造结点的结构体 typedef struct BiTNode{ TElemType data;//数据域 struct BiTNode *lchild,*rchild;//左右孩子指针 }BiTNode,*BiTree; //初始化树的函数 void CreateBiTree(BiTree *T){ *T=(BiTNode*)malloc(sizeof(BiTNode)); (*T)->data=1; (*T)->lchild=(BiTNode*)malloc(sizeof(BiTNode)); (*T)->rchild=(BiTNode*)malloc(sizeof(BiTNode)); (*T)->lchild->data=2; (*T)->lchild->lchild=(BiTNode*)malloc(sizeof(BiTNode)); (*T)->lchild->rchild=(BiTNode*)malloc(sizeof(BiTNode)); (*T)->lchild->rchild->data=5; (*T)->lchild->rchild->lchild=NULL; (*T)->lchild->rchild->rchild=NULL; (*T)->rchild->data=3; (*T)->rchild->lchild=(BiTNode*)malloc(sizeof(BiTNode)); (*T)->rchild->lchild->data=6; (*T)->rchild->lchild->lchild=NULL; (*T)->rchild->lchild->rchild=NULL; (*T)->rchild->rchild=(BiTNode*)malloc(sizeof(BiTNode)); (*T)->rchild->rchild->data=7; (*T)->rchild->rchild->lchild=NULL; (*T)->rchild->rchild->rchild=NULL; (*T)->lchild->lchild->data=4; (*T)->lchild->lchild->lchild=NULL; (*T)->lchild->lchild->rchild=NULL; } //前序和中序遍历使用的进栈函数 void push(BiTNode** a,BiTNode* elem){ a[++top]=elem; } //弹栈函数 void pop( ){ if (top==-1) { return ; } top--; } //模拟操作结点元素的函数,输出结点本身的数值 void displayElem(BiTNode* elem){ printf("%d ",elem->data); } //拿到栈顶元素 BiTNode* getTop(BiTNode**a){ return a[top]; } //中序遍历非递归算法 void InOrderTraverse1(BiTree Tree){ BiTNode* a[20];//定义一个顺序栈 BiTNode * p;//临时指针 push(a, Tree);//根结点进栈 while (top!=-1) {//top!=-1说明栈内不为空,程序继续运行 while ((p=getTop(a)) &&p){//取栈顶元素,且不能为NULL push(a, p->lchild);//将该结点的左孩子进栈,如果没有左孩子,NULL进栈 } pop();//跳出循环,栈顶元素肯定为NULL,将NULL弹栈 if (top!=-1) { p=getTop(a);//取栈顶元素 pop();//栈顶元素弹栈 displayElem(p); push(a, p->rchild);//将p指向的结点的右孩子进栈 } } } //中序遍历实现的另一种方法 void InOrderTraverse2(BiTree Tree){ BiTNode* a[20];//定义一个顺序栈 BiTNode * p;//临时指针 p=Tree; //当p为NULL或者栈为空时,表明树遍历完成 while (p || top!=-1) { //如果p不为NULL,将其压栈并遍历其左子树 if (p) { push(a, p); p=p->lchild; } //如果p==NULL,表明左子树遍历完成,需要遍历上一层结点的右子树 else{ p=getTop(a); pop(); displayElem(p); p=p->rchild; } } } int main(){ BiTree Tree; CreateBiTree(&Tree); printf("中序遍历算法1: \n"); InOrderTraverse1(Tree); printf("\n中序遍历算法2: \n"); InOrderTraverse2(Tree); } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100

【 6. 二叉树的后序遍历 】
- 二叉树后序遍历的实现思想是:从根节点出发,依次遍历各节点的左右子树,直到当前节点左右子树遍历完成后,才访问该节点元素。
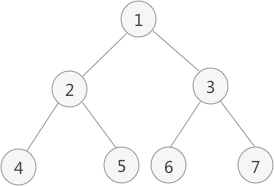
- 上图中二叉树进行后序遍历的结果为:4 5 2 6 7 3 1
- 如上图中,对此二叉树进行后序遍历的操作过程为:
从根节点 1 开始,遍历该节点的左子树(以节点 2 为根节点);
遍历节点 2 的左子树(以节点 4 为根节点);
由于节点 4 既没有左子树,也没有右子树,此时访问该节点中的元素 4,并回退到节点 2 ,遍历节点 2 的右子树(以 5 为根节点);
由于节点 5 无左右子树,因此可以访问节点 5 ,并且此时节点 2 的左右子树也遍历完成,因此也可以访问节点 2;
此时回退到节点 1 ,开始遍历节点 1 的右子树(以节点 3 为根节点);
遍历节点 3 的左子树(以节点 6 为根节点);
由于节点 6 无左右子树,因此访问节点 6,并回退到节点 3,开始遍历节点 3 的右子树(以节点 7 为根节点);
由于节点 7 无左右子树,因此访问节点 7,并且节点 3 的左右子树也遍历完成,可以访问节点 3;节点 1 的左右子树也遍历完成,可以访问节点 1;
到此,整棵树的遍历结束。
6.1 递归实现
- 后序遍历的递归实现C代码为:
#include#include #include //构造结点的结构体 typedef struct BiTNode { int data;//数据域 struct BiTNode* lchild, * rchild;//左右孩子指针 }BiTNode, * BiTree; //模拟操作结点元素的函数,输出结点本身的数值 void displayElem(BiTNode* elem) { printf("%d ", elem->data); } //后序遍历 void PostOrderTraverse(BiTree T) { if (T) { PostOrderTraverse(T->lchild);//遍历左孩子 PostOrderTraverse(T->rchild);//遍历右孩子 displayElem(T);//调用操作结点数据的函数方法 } //如果结点为空,返回上一层 return; } void CreateBiTree(BiTree* T); int main() { BiTree Tree; CreateBiTree(&Tree); printf("后序遍历: \n"); PostOrderTraverse(Tree); } //初始化树的函数 void CreateBiTree(BiTree* T) { *T = (BiTNode*)malloc(sizeof(BiTNode)); (*T)->data = 1; (*T)->lchild = (BiTNode*)malloc(sizeof(BiTNode)); (*T)->rchild = (BiTNode*)malloc(sizeof(BiTNode)); (*T)->lchild->data = 2; (*T)->lchild->lchild = (BiTNode*)malloc(sizeof(BiTNode)); (*T)->lchild->rchild = (BiTNode*)malloc(sizeof(BiTNode)); (*T)->lchild->rchild->data = 5; (*T)->lchild->rchild->lchild = NULL; (*T)->lchild->rchild->rchild = NULL; (*T)->rchild->data = 3; (*T)->rchild->lchild = (BiTNode*)malloc(sizeof(BiTNode)); (*T)->rchild->lchild->data = 6; (*T)->rchild->lchild->lchild = NULL; (*T)->rchild->lchild->rchild = NULL; (*T)->rchild->rchild = (BiTNode*)malloc(sizeof(BiTNode)); (*T)->rchild->rchild->data = 7; (*T)->rchild->rchild->lchild = NULL; (*T)->rchild->rchild->rchild = NULL; (*T)->lchild->lchild->data = 4; (*T)->lchild->lchild->lchild = NULL; (*T)->lchild->lchild->rchild = NULL; } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
6.2 非递归实现
- 递归算法底层的实现使用的是栈存储结构,所以可以直接使用栈写出相应的非递归算法。
- 后序遍历是在遍历完当前结点的左右孩子之后,才调用操作函数,所以需要在操作结点进栈时,为每个结点配备一个标志位。当遍历该结点的左孩子时,设置当前结点的标志位为 0,进栈;当要遍历该结点的右孩子时,设置当前结点的标志位为 1,进栈。
这样,当遍历完成,该结点弹栈时,查看该结点的标志位的值:如果是 0,表示该结点的右孩子还没有遍历;反之如果是 1,说明该结点的左右孩子都遍历完成,可以调用操作函数。 - C 实现
#include#include #include int top = -1;//top变量时刻表示栈顶元素所在位置 //构造结点的结构体 typedef struct BiTNode { int data;//数据域 struct BiTNode* lchild, * rchild;//左右孩子指针 }BiTNode, * BiTree; //弹栈函数 void pop() { if (top == -1) { return; } top--; } //模拟操作结点元素的函数,输出结点本身的数值 void displayElem(BiTNode* elem) { printf("%d ", elem->data); } //后序遍历非递归算法 typedef struct SNode { BiTree p; int tag; }SNode; //后序遍历使用的进栈函数 void postpush(SNode* a, SNode sdata) { a[++top] = sdata; } //后序遍历函数 void PostOrderTraverse(BiTree Tree) { SNode a[20];//定义一个顺序栈 BiTNode* p;//临时指针 int tag; SNode sdata; p = Tree; while (p || top != -1) { while (p) { //为该结点入栈做准备 sdata.p = p; sdata.tag = 0;//由于遍历是左孩子,设置标志位为0 postpush(a, sdata);//压栈 p = p->lchild;//以该结点为根结点,遍历左孩子 } sdata = a[top];//取栈顶元素 pop();//栈顶元素弹栈 p = sdata.p; tag = sdata.tag; //如果tag==0,说明该结点还没有遍历它的右孩子 if (tag == 0) { sdata.p = p; sdata.tag = 1; postpush(a, sdata);//更改该结点的标志位,重新压栈 p = p->rchild;//以该结点的右孩子为根结点,重复循环 } //如果取出来的栈顶元素的tag==1,说明此结点左右子树都遍历完了,可以调用操作函数了 else { displayElem(p); p = NULL; } } } void CreateBiTree(BiTree* T); int main() { BiTree Tree; CreateBiTree(&Tree); printf("后序遍历: \n"); PostOrderTraverse(Tree); } //初始化树的函数 void CreateBiTree(BiTree* T) { *T = (BiTNode*)malloc(sizeof(BiTNode)); (*T)->data = 1; (*T)->lchild = (BiTNode*)malloc(sizeof(BiTNode)); (*T)->rchild = (BiTNode*)malloc(sizeof(BiTNode)); (*T)->lchild->data = 2; (*T)->lchild->lchild = (BiTNode*)malloc(sizeof(BiTNode)); (*T)->lchild->rchild = (BiTNode*)malloc(sizeof(BiTNode)); (*T)->lchild->rchild->data = 5; (*T)->lchild->rchild->lchild = NULL; (*T)->lchild->rchild->rchild = NULL; (*T)->rchild->data = 3; (*T)->rchild->lchild = (BiTNode*)malloc(sizeof(BiTNode)); (*T)->rchild->lchild->data = 6; (*T)->rchild->lchild->lchild = NULL; (*T)->rchild->lchild->rchild = NULL; (*T)->rchild->rchild = (BiTNode*)malloc(sizeof(BiTNode)); (*T)->rchild->rchild->data = 7; (*T)->rchild->rchild->lchild = NULL; (*T)->rchild->rchild->rchild = NULL; (*T)->lchild->lchild->data = 4; (*T)->lchild->lchild->lchild = NULL; (*T)->lchild->lchild->rchild = NULL; } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
【 7. 二叉树的层次遍历 】
- 层次遍历:按照二叉树中的层次从左到右依次遍历每层中的结点。
- 具体的实现思路是:通过使用队列的数据结构,从树的根结点开始,依次将其左孩子和右孩子入队。而后每次队列中一个结点出队,都将其左孩子和右孩子入队,直到树中所有结点都出队,出队结点的先后顺序就是层次遍历的最终结果。
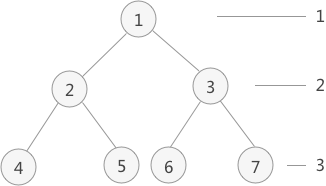
- 例如,层次遍历上图中的二叉树:
首先,根结点 1 入队→[1];
根结点 1 出队→[],出队的同时,将左孩子 2 和右孩子 3 分别入队→[2 3];
队头结点 2 出队→[3],出队的同时,将结点 2 的左孩子 4 和右孩子 5 依次入队→[3 4 5];
队头结点 3 出队→[4 5],出队的同时,将结点 3 的左孩子 6 和右孩子 7 依次入队→[4 5 6 7];
不断地循环,直至队列内为空。
出队次序依次为:1 2 3 4 5 6 7
- C实现
#include#include //初始化队头和队尾指针开始时都为0 int front = 0, rear = 0; typedef struct BiTNode { int data;//数据域 struct BiTNode* lchild, * rchild;//左右孩子指针 }BiTNode, * BiTree; //入队函数 void EnQueue(BiTree* a, BiTree node) { a[rear++] = node; } //出队函数 BiTNode* DeQueue(BiTNode** a) { return a[front++]; } //输出函数 void displayNode(BiTree node) { printf("%d ", node->data); } void CreateBiTree(BiTree* T); int main() { BiTree tree; //初始化二叉树 CreateBiTree(&tree); BiTNode* p; //采用顺序队列,初始化创建队列数组 BiTree a[20]; //根结点入队 EnQueue(a, tree); //当队头和队尾相等时,表示队列为空 while (front < rear) { //队头结点出队 p = DeQueue(a); displayNode(p); //将队头结点的左右孩子依次入队 if (p->lchild != NULL) { EnQueue(a, p->lchild); } if (p->rchild != NULL) { EnQueue(a, p->rchild); } } return 0; } void CreateBiTree(BiTree* T) { *T = (BiTNode*)malloc(sizeof(BiTNode)); (*T)->data = 1; (*T)->lchild = (BiTNode*)malloc(sizeof(BiTNode)); (*T)->rchild = (BiTNode*)malloc(sizeof(BiTNode)); (*T)->lchild->data = 2; (*T)->lchild->lchild = (BiTNode*)malloc(sizeof(BiTNode)); (*T)->lchild->rchild = (BiTNode*)malloc(sizeof(BiTNode)); (*T)->lchild->rchild->data = 5; (*T)->lchild->rchild->lchild = NULL; (*T)->lchild->rchild->rchild = NULL; (*T)->rchild->data = 3; (*T)->rchild->lchild = (BiTNode*)malloc(sizeof(BiTNode)); (*T)->rchild->lchild->data = 6; (*T)->rchild->lchild->lchild = NULL; (*T)->rchild->lchild->rchild = NULL; (*T)->rchild->rchild = (BiTNode*)malloc(sizeof(BiTNode)); (*T)->rchild->rchild->data = 7; (*T)->rchild->rchild->lchild = NULL; (*T)->rchild->rchild->rchild = NULL; (*T)->lchild->lchild->data = 4; (*T)->lchild->lchild->lchild = NULL; (*T)->lchild->lchild->rchild = NULL; } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 满足以下两个条件的树就是 二叉树:
-
相关阅读:
springboot+nodejs+vue网上选课系统
神经网络 卷积神经网络,卷积神经网络训练太慢
PlacementTools...
深度强化学习入门:马尔可夫决策过程(井字棋案例理解)
「运维有小邓」审核并分析文件和文件夹访问权限
MySQL中表的设计
无人机的工作原理
什么是设计模式?
《卡拉马佐夫兄弟》人物表
Mysql 45讲学习笔记(三十八)Memory引擎
- 原文地址:https://blog.csdn.net/qq_44431690/article/details/138139942
