AC自动机

AC自动机

前置芝士

1. kmp
2. trie

介绍

学算法首先肯定要清楚这个算法是用来解决啥东西的。

AC 自动机是用线性的复杂度来解决多模匹配的算法。
额(⊙o⊙)，说人话就是例如给你一堆字符串（称为模式串）和一个字符串（称为文本串），让你求模式串们在文本串出现的总次数。

来直接看模板题：

AC 自动机（简单版）

题目描述

给定 $n$ 个模式串 $s_i$ 和一个文本串 $t$，求有多少个不同的模式串在文本串里出现过。
两个模式串不同当且仅当他们编号不同。

对于 $100\mathrm{\%}$ 的数据，保证 $1\le n\le {10}^6$，$1\le |t|\le {10}^6$，$1\le \sum _{i=1}^n|s_i|\le {10}^6$。$s_i,t$ 中仅包含小写字母。

那么好，现在应该很清楚了，这不就是 kmp 的模板题中模式串变多了亿点点吗？如果每个模式串分开匹配，平方级别复杂度，直接爆炸。众所周知：

$$AC\mathrm{自}\mathrm{动}\mathrm{机}=trie+kmp$$

我们要做的是把所有的模式串建立一个 trie，然后在 trie 上跑 kmp。

可以回想一下 kmp 匹配的过程。有一个数组 $fail$，或者是 $next$（以下简称为 $f$）。

它的含义有很多，本质上 $f[i]$ 是指：模式串 $s$ 的下标为 $i$ 的位置失配时，模式串的指针应该返回的下标。

如果将 $f$ 数组的所有值向前移动一位，那么他的含义就可以变为：在以 $s[i]$ 结尾的前缀中，它的真后缀能匹配到的最长前缀的长度。这也是我们求 $f$ 数组的关键。

这样的话，在失配的情况下，指针回跳的次数就能最少，可以保证线性的复杂度。

类比一下，trie 上的 kmp 也是一样的 $f[i]$ 是指：下标为 $i$ 的位置失配时，模式串的指针应该返回的下标。

现在已经匹配完了节点 $i$，接下来要匹配它的子节点，如果失配（或者匹配完了），说明这一条路就不必继续走了，要换一条。而从根节点到 $i$ 都是匹配的，我就可以跳到 $j$ 上，使得 $root$ 到 $j$ 是 $root$ 到 $i$ 的真后缀能匹配到的从根开始的最长前缀，以保证回跳次数最少。

是不是和 kmp 几乎一样？这样，跳到 $j$ 的位置，继续匹配 $j$ 的子节点。其实就是在匹配一个模式串时不行，直接换一个继续。都不行就返回根从头来过。这样解释就十分贴切于 kmp 了。

kmp 其实可以看作 trie 为一条链的 AC 自动机。

举个例子：

highlighter- mipsasm

she
he
say
shr
her

trie 图为：

绿色的箭头就是 $fail$ 指针，根据定义：

highlighter- apache

f[2]=4
f[3]=5
f[6]=0

比如在二号节点失配，那么 $s$ 和 $h$ 肯定是匹配好了的，所以返回四号节点，继续匹配。

操作

insert

主要就是建立 trie 的过程，和模板一样的，就不多解释了。

cpp

// 这里p为下标，tr为节点编号，tot为节点总数
void insert(string x)
{
    int p=0;
    for(auto c:x)
    {
        int u=c-'a';
        if(!tr[p][u]) tr[p][u]=++tot;
        p=tr[p][u];
    }
    cnt[p]++;//这里要视情况而定
}

build

$fail$ 的含义上面已经说清楚了，现在就要解决如何去求得 $fail$ 数组。

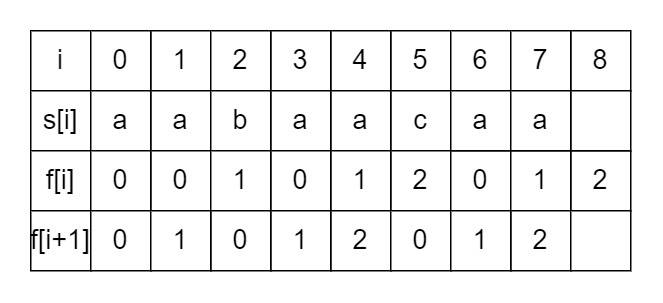
先看到 kmp 是如何求的：

cpp

int i=1,j=0;
while(isize())
{
    //j=f[i-1];
	while(j&&s[i]!=s[j]) j=f[j];
	if(s[i]==s[j]) j++;
	f[++i]=j;
}

当然会有其他的写法，不过也大同小异。注意看注释掉的一行，注释的原因是因为这就是我们上一次循环求得的 $j$，不需要再赋一遍值。但加上后这个过程就会更加清晰。

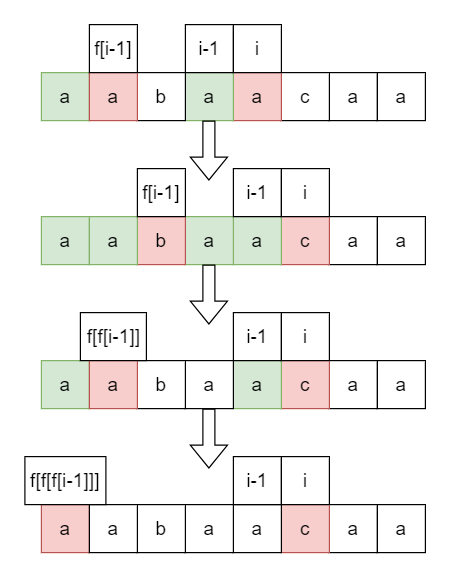
还是拿这个例子。

绿色表示已经匹配好了的可以继续用的，红色表示即将要匹配的。

可以看到，要是红色的匹配成功了，自然绿色部分长度加一；若是不成功，就要保证 $i$ 位置上前面的绿色部分尽可能多，所以再跳一次。不行的话，继续跳，直到 $0$ 也不成功。这时 $f[i]=0$。

也就是说我们要用到上一个位置的 $f$ 值，递推的去求。而在 trie 上，就可以用 BFS 逐层去求 $f$ 数组。

至于代码，直接对应 kmp 写就好了，注意第一层的 $f$ 肯定是 $0$。

cpp

queue<int> q;
void build()
{
    for(int i=0;i<26;i++) 
        if(tr[0][i])
            q.push(tr[0][i]);//根的儿子都为0，直接入队
    while(!q.empty())
    {
        int u=q.front();q.pop();
        for(int i=0;i<26;i++)//遍历下一层的所有儿子
        {
            int v=tr[u][i],j=f[u];//j=f[i-1];
            while(j&&!tr[j][i]) j=f[j];//while(j&&s[i]!=s[j]) j=f[j];
            if(tr[j][i]) j=tr[j][i];//if(s[i]==s[j]) j++;
            f[v]=j;//f[++i]=j;
        }
    }
}

一模一样对吧？等一等，怎么感觉不太对，为啥别人的代码没有 for 里面的 while？

其实 AC 自动机有一个优化，就是把这个 while 优化掉的。优化后也叫做 trie 图。也就是我们一般所写的形式，统称为 AC 自动机。优化只是优化常数，优化前后其实都是线性的复杂度。

那么好，问题就在于 while。匹配 $u$ 的儿子 $i$ 的时候 $f[u]$ 的儿子里没有 $i$，就要往上跳。

这里就可以用类似并查集中路径压缩的方法，将信息存在没有的虚点中，在匹配失败后对号入座就好了。

cpp

queue<int> q;
void build()
{
    for(int i=0;i<26;i++) 
        if(tr[0][i])
            q.push(tr[0][i]);
    while(!q.empty())
    {
        int u=q.front();q.pop();
        for(int i=0;i<26;i++)
        {
            int v=tr[u][i];
            if(!v) tr[u][i]=tr[f[u]][i];//若失败，继承信息
            else f[v]=tr[f[u]][i],q.push(v);//若成功，直接赋值
        }
    }
}

这就是 AC 自动机建立的终极形态 QWQ。

查询

明白了重点以后，这个就简单很多了，也是由 kmp 的代码直接推过来。

为避免重复，用 $-1$ 来标记。

只不过当匹配到一个后，它的前缀也要统计答案，而前缀中可能出现的都应该在 $f$ 里面，所以一直跳直到根统计答案就好了。

cpp

int query(string x)
{
    int p=0,ans=0;
    for(auto c:x)
    {
        int u=c-'a';
        while(p&&!tr[p][u]) p=f[p];//while(j&&t[i]!=s[j]) j=f[j];
        if(tr[p][u]) p=tr[p][u];//if(t[i]==s[j]) j++;

        int j=p;
        while(j&&cnt[j]!=-1)
        {
            ans+=cnt[j]；
            cnt[j]=-1;
            j=f[j];
        }
    }
    return ans;
}

和 build 同理，这也可以优化，就直接变成了：

cpp

int query(string x)
{
    int p=0,ans=0;
    for(auto c:x)
    {
        int u=c-'a';
        p=tr[p][u];//省去while
        int j=p;
        while(j&&cnt[j]!=-1)
        {
            ans+=cnt[j]；
            cnt[j]=-1;
            j=f[j];
        }
    }
    return ans;
}

code

完整代码：

cpp

#include 
using namespace std;
const int N=1e6+5;

queue<int> q;
int n,tot;
int tr[N][26],cnt[N],f[N];
string s;
void insert(string x)
{
    int p=0;
    for(auto c:x)
    {
        int u=c-'a';
        if(!tr[p][u]) tr[p][u]=++tot;
        p=tr[p][u];
    }
    cnt[p]++;
}
void build()
{
    for(int i=0;i<26;i++) 
        if(tr[0][i])
            q.push(tr[0][i]);
    while(!q.empty())
    {
        int u=q.front();q.pop();
        for(int i=0;i<26;i++)
        {
            int v=tr[u][i];
            if(!v) tr[u][i]=tr[f[u]][i];
            else f[v]=tr[f[u]][i],q.push(v);
        }
    }
}
int query(string x)
{
    int p=0,ans=0;
    for(auto c:x)
    {
        int u=c-'a';
        p=tr[p][u];
        int j=p;
        while(j&&cnt[j]!=-1)
        {
            ans+=cnt[j];
            cnt[j]=-1;
            j=f[j];
        }
    }
    return ans;
}
int main ()
{
    cin>>n;
    for(int i=1;i<=n;i++) 
    {
        cin>>s;
        insert(s);
    }
    build();
    cin>>s;
    cout<<query(s)<<"\n";
    return 0;
}

拓扑建图优化

代填的坑 qwq。

一些心得体会

算法学习中，有些可以半懂不懂，比如 kmp，了解 $fail$ 是啥，怎么写代码就行了，这样反而会更轻松。而有些若想要融汇贯通，则必须充分理解，才能应用到题目中。

写博客总结的过程中，可以顺便梳理整个过程。带着想要教会别人的目标，不知不觉间自己也能更加深刻地理解。更何况，认真写出一篇博客后，成就感是真真切切的。

前路漫漫，未到抬头之时，我只需，低头前行。

• AC自动机
•     前置芝士
•     介绍
•         题目描述
•     操作
•         insert
•         build
•         查询
•         code
•     拓扑建图优化
•     一些心得体会

__EOF__