-
深度学习--神经网络基础(2)
损失函数
在深度学习中, 损失函数是用来衡量模型参数的质量的函数 , 衡量的方式是比较网络输出和真实输出的差异:
分类
1.多分类损失函数
在多分类任务通常使用 softmax 将 logits 转换为概率的形式,所以多分类的交叉熵损失也叫做 softmax 损失 ,它的计算方法是: 其中:1. y 是样本 x 属于某一个类别的真实概率2. 而 f(x) 是样本属于某一类别的预测分数3. S 是 softmax 激活函数 , 将属于某一类别的预测分数转换成概率4. L 用来衡量真实值 y 和预测值 f(x) 之间差异性的损失结果
其中:1. y 是样本 x 属于某一个类别的真实概率2. 而 f(x) 是样本属于某一类别的预测分数3. S 是 softmax 激活函数 , 将属于某一类别的预测分数转换成概率4. L 用来衡量真实值 y 和预测值 f(x) 之间差异性的损失结果2.二分类任务损失交叉熵
在处理二分类任务时,我们不再使用softmax激活函数,而是使用sigmoid激活函数,那损失函数也相应的进行调整, 使用二分类的交叉熵损失函数: 其中:1. y是样本x属于某一个类别的真实概率2. 而y^是样本属于某一类别的预测概率3. L用来衡量真实值y与预测值y^之间差异性的损失结果。
其中:1. y是样本x属于某一个类别的真实概率2. 而y^是样本属于某一类别的预测概率3. L用来衡量真实值y与预测值y^之间差异性的损失结果。3.回归任务损失函数
MAE损失函数
Mean absolute loss(MAE)也被称为L1 Loss,是以绝对误差作为距离。损失函数公式:
 曲线如下图所示:
曲线如下图所示: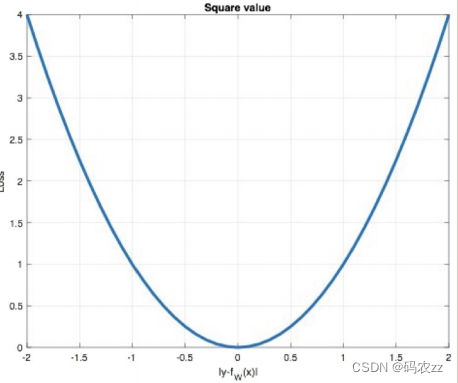 特点是:1. 由于L1 loss具有稀疏性,为了惩罚较大的值,因此常常将其作为 正则项添加到其他loss中作为约束。2. L1 loss的最大问题是梯度在零点不平滑,导致会跳过极小值。
特点是:1. 由于L1 loss具有稀疏性,为了惩罚较大的值,因此常常将其作为 正则项添加到其他loss中作为约束。2. L1 loss的最大问题是梯度在零点不平滑,导致会跳过极小值。MSE损失函数
Mean Squared Loss/ Quadratic Loss(MSE loss) 也被称为L2 loss,或欧氏距离,它以误差的平方和的均值作为距离,损失函数公式: 曲线如下图所示:
曲线如下图所示: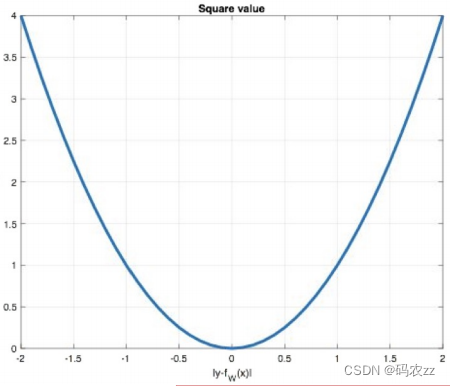 特点是:1. L2 loss也常常作为正则项。2. 当预测值与目标值相差很大时, 梯度容易爆炸。
特点是:1. L2 loss也常常作为正则项。2. 当预测值与目标值相差很大时, 梯度容易爆炸。Smooth L1损失函数
smooth L1 说的是光滑之后的 L1 。损失函数公式 :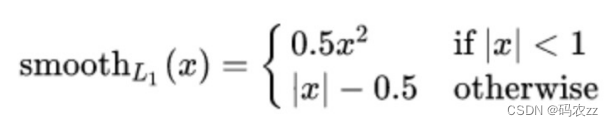 其中: ? =f(x)−y 为真实值和预测值的差值。
其中: ? =f(x)−y 为真实值和预测值的差值。 从上图中可以看出,该函数实际上就是一个分段函数1. 在 [-1,1] 之间实际上就是 L2 损失,这样解决了 L1 的不光滑问题2. 在 [-1,1] 区间外,实际上就是 L1 损失,这样就解决了离群点梯度爆炸的问题
从上图中可以看出,该函数实际上就是一个分段函数1. 在 [-1,1] 之间实际上就是 L2 损失,这样解决了 L1 的不光滑问题2. 在 [-1,1] 区间外,实际上就是 L1 损失,这样就解决了离群点梯度爆炸的问题代码示例
- import torch
- # 1. 多任务交叉熵损失
- # 设置真实值: 可以是热编码后的结果也可以不进行热编码
- # 注意的类型必须是64位整型数据
- # y_true = torch.tensor([1,2],dtype=torch.int64)
- y_true = torch.tensor([[0, 1, 0], [0, 0, 1]], dtype=torch.float32)
- y_pred = torch.tensor([[1,10,1],[2,3,10]],dtype=torch.float32)
- # 实例化多任务交叉熵损失
- L= torch.nn.CrossEntropyLoss()
- # 计算损失结果
- print(L(y_pred,y_true))
- # 2. 二分类的交叉熵
- y_true = torch.tensor([0,0,1],dtype=torch.float32)
- y_pred = torch.tensor([0.01,0.02,0.7],dtype=torch.float32)
- # 二分类交叉熵损失
- L= torch.nn.BCELoss()
- print(L(y_pred,y_true))
- # 3. 回归任务
- y_true = torch.tensor([2.0,0.5,10],dtype=torch.float32)
- # y_pred = torch.tensor([2,8,0.9],dtype=torch.float32)
- y_pred = torch.tensor([2,0.8,9],dtype=torch.float32)
- # L =torch.nn.L1Loss()
- # L =torch.nn.MSELoss()
- L =torch.nn.SmoothL1Loss()
- print(L(y_pred,y_true))
高级数字化帝都下降人才培训专家梯度下降优化方法
梯度下降优化算法中,可能会碰到以下情况:1. 碰到平缓区域,梯度值较小,参数优化变慢2. 碰到 “鞍点” ,梯度为 0,参数无法优化3. 碰到局部最小值,参数不是最优对于这些问题, 出现了一些对梯度下降算法的优化方法,例如:Momentum、AdaGrad、RMSprop、Adam 等
指数加权平均
指数移动加权平均 则是参考各数值,并且各数值的权重都不同,距离越远的数字对平均数计算的贡献就越小(权重较小),距离越近则对平均数的计算贡献就越大(权重越大)。比如:明天气温怎么样,和昨天气温有很大关系,而和一个月前的气温关系就小一些。计算公式可以用下面的式子来表示: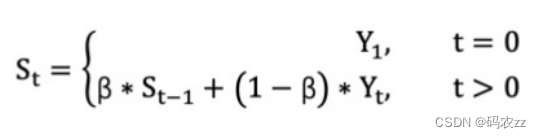 • St 表示指数加权平均值 ;• Yt 表示 t 时刻的值 ;• β 调节权重系数,该值越大平均数越平缓。下面通过代码来看结果,随机产生 30 天的气温数据:
• St 表示指数加权平均值 ;• Yt 表示 t 时刻的值 ;• β 调节权重系数,该值越大平均数越平缓。下面通过代码来看结果,随机产生 30 天的气温数据: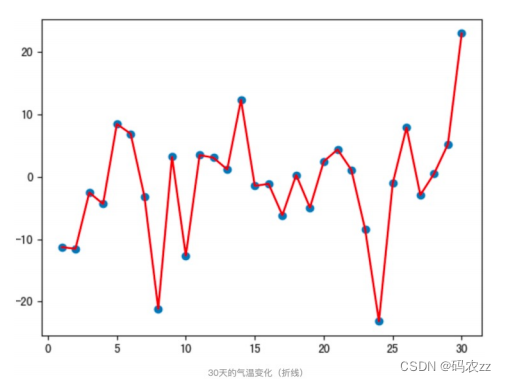
- import torch
- import matplotlib.pyplot as plt
- # 产生30天的随机温度
- temperature = torch.randn([30,]) * 10
- # 绘制平均温度
- x = torch.arange(0,30,1)
- plt.scatter(x,temperature)
- # 指数加权平均
- exp = [] # 指数加权后的值
- beta = 0.9
- for idx,tmp in enumerate(temperature):
- # 第一个元素的的 EWA 值等于自身
- if idx ==0:
- exp.append(tmp)
- continue
- # 第二个元素的 EWA 值等于上一个 EWA 乘以 β + 当前气温乘以 (1-β)
- t = beta * exp[idx-1] + (1-beta) * tmp
- exp.append(t)
- plt.scatter(x,temperature)
- plt.plot(x,exp)
- plt.show()
 上图是 β 为 0.5 和 0.9 时的结果,从中可以看出:• 指数加权平均绘制出的气氛变化曲线更加平缓,• β 的值越大,则绘制出的折线越加平缓,波动越小。
上图是 β 为 0.5 和 0.9 时的结果,从中可以看出:• 指数加权平均绘制出的气氛变化曲线更加平缓,• β 的值越大,则绘制出的折线越加平缓,波动越小。动量算法Momentum
梯度计算公式:Dt = β * St-1 + (1- β) * Wt1. St-1 表示历史梯度移动加权平均值2. Wt 表示当前时刻的梯度值3. Dt 为当前时刻的指数加权平均梯度值4. β 为权重系数假设:权重 β 为 0.9,例如:第一次梯度值:s1 = d1 = w1第二次梯度值:d2=s2 = 0.9 * s1 + w2 * 0.1第三次梯度值:d3=s3 = 0.9 * s2 + w3 * 0.1第四次梯度值:d4=s4 = 0.9 * s3 + w4 * 0.1梯度下降公式中梯度的计算,就不再是当前时刻 t 的梯度值,而是历史梯度值的指数移动加权平均值。公式修改为:W_t+1 = W_t - a * Dtadagrad
AdaGrad 通过对不同的参数分量使用不同的学习率, AdaGrad 的学习率总体会逐渐减小 。其计算步骤如下:1. 初始化学习率 α 、初始化参数 θ 、小常数 σ = 1e-62. 初始化梯度累积变量 s = 03. 从训练集中采样 m 个样本的小批量,计算梯度 g4. 累积平方梯度 s = s + g ⊙ g , ⊙ 表示各个分量相乘学习率 α 的计算公式如下:参数更新公式如下: 重复 2-4 步骤 , 即可完成网络训练。AdaGrad 缺点是可能会使得学习率过早、过量的降低,导致模型训练后期学习率太小,较难找到最优解。
重复 2-4 步骤 , 即可完成网络训练。AdaGrad 缺点是可能会使得学习率过早、过量的降低,导致模型训练后期学习率太小,较难找到最优解。RMSProp
RMSProp 优化算法是对 AdaGrad 的优化 . 最主要的不同是,其使用 指数移动加权平均梯度 替换历史梯度 的平方和。其计算过程如下:1. 初始化学习率 α 、初始化参数 θ 、小常数 σ = 1e-62. 初始化参数 θ3. 初始化梯度累计变量 s4. 从训练集中采样 m 个样本的小批量,计算梯度 g5. 使用指数移动平均累积历史梯度,公式如下: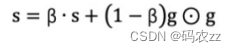 学习率 α 的计算公式如下:
学习率 α 的计算公式如下: 参数更新公式如下:高级数字化人才培训
参数更新公式如下:高级数字化人才培训 专家
专家
Adam
-Momentum 使用指数加权平均计算当前的梯度值-AdaGrad、RMSProp 使用自适应的学习率-Adam优化算法(Adaptive Moment Estimation,自适应矩估计)将 Momentum 和RMSProp 算法结合在一起。1.修正梯度: 使⽤ 梯度的指数加权平均2.修正学习率: 使⽤ 梯度平 ⽅ 的指数加权平均 。代码示例
- import torch
- from torch import optim
- # 1. SGD
- # 初始化权重参数
- w = torch.tensor([1.0],requires_grad=True)
- y = (w**2/2.0).sum() # 损失函数
- # 优化方法:SGD指定参数beta(momentum)
- # optimizer = optim.SGD([w],lr=0.01,momentum=0.9)
- # 优化方法: Adagrad
- # optimizer = optim.Adagrad([w],lr=0.01)
- # 优化方法: RMSProp
- optimizer = optim.RMSprop([w],lr=0.01,alpha=0.9)
- # 优化方法:Adam
- optimizer = optim.Adam([w],lr=0.01,betas=[0.9,0.99])
- # 第一次更新计算梯度,并对参数进行更新
- optimizer.zero_grad() # 梯度清零
- y.backward() # 自动微分
- optimizer.step() # 更新权重
- # 打印结果
- print(w.detach().numpy()) # w本身
- print(w.grad.numpy()) # 梯度结果
- # 第二次更新计算梯度,并对参数进行更新
- y = (w**2/2.0).sum()
- optimizer.zero_grad() # 梯度清零
- y.backward() # 自动微分
- optimizer.step() # 更新权重
- # 打印结果
- print(w.detach().numpy())
- print(w.grad.numpy())
学习率衰减方法
等间隔学习率衰减

指定间隔学习率衰减

按指数学习率衰减

代码示例
- import torch
- import matplotlib.pyplot as plt
- # 初始化参数
- y_true = torch.tensor([0.1])
- w = torch.tensor([1.0],requires_grad=True)
- x = torch.tensor([1.0])
- # 设置优化器
- optimizer = torch.optim.SGD([w],lr=0.1,momentum=0.9)
- # 设置间隔学习率下降策略 step_size:调整间隔数=50 , gamma:调整系数
- lr_s = torch.optim.lr_scheduler.StepLR(optimizer,step_size=20,gamma=0.1)
- # 设置指定间隔学习率下降策略 milestones:设定调整轮次 , gamma:调整系数
- # lr_s = torch.optim.lr_scheduler.MultiStepLR(optimizer,milestones=[50, 125, 160],gamma=0.1)
- # 设置指数学习率下降策略 gamma:指数的底
- # lr_s = torch.optim.lr_scheduler.ExponentialLR(optimizer,gamma=0.98)
- # 获取学习率和当前的epoch
- lr_list = [] # 学习率
- for epoch in range(200): # 轮次
- lr_list.append(lr_s.get_last_lr()) # get_last_lr 提取学习率
- for i in range(10): # 批次
- loss = (w*x-y_true)**2/2.0 # 损失函数
- optimizer.zero_grad() # 梯度清零
- loss.backward() # 自动微分
- optimizer.step() # 更新权重
- # 更新下一个epoch的学习率
- lr_s.step()
- plt.plot(torch.arange(0,200),lr_list)
- plt.grid()
- plt.show()
正则化
 在设计机器学习算法时希望在新样本上的泛化能力强。许多机器学习算法都采用相关的策略来减小测试误差,这些策 略被统称为正则化。• 神经网络的强大的表示能力经常遇到过拟合,所以需要使用不同形式的正则化策略。• 目前在深度学习中使用较多的策略有 范数惩罚, DropOut ,特殊的网络层等
在设计机器学习算法时希望在新样本上的泛化能力强。许多机器学习算法都采用相关的策略来减小测试误差,这些策 略被统称为正则化。• 神经网络的强大的表示能力经常遇到过拟合,所以需要使用不同形式的正则化策略。• 目前在深度学习中使用较多的策略有 范数惩罚, DropOut ,特殊的网络层等DropOut
在练神经网络中模型参数较多,在数据量不足的情况下,很容易过拟合。 Dropout (随机失活)是一个简单有效的正则 化方法。 • 在训练过程中, Dropout 的实现是 让神经元以超参数 p 的概率停止工作或者激活被置为 0, 未被置为 0 的进行缩放,缩放 比例为 1/(1-p) 。训练过程可以认为是对完整的神经网络的一些子集进行训练,每次基于输入数据只更新子网络的参数• 在测试过程中,随机失活不起作用。
• 在训练过程中, Dropout 的实现是 让神经元以超参数 p 的概率停止工作或者激活被置为 0, 未被置为 0 的进行缩放,缩放 比例为 1/(1-p) 。训练过程可以认为是对完整的神经网络的一些子集进行训练,每次基于输入数据只更新子网络的参数• 在测试过程中,随机失活不起作用。 -
相关阅读:
Ui自动化测试如何上传文件
论人类下一代语言的可能—4.1算术
【项目小tips】登录状态存储
好题分享
SAML tracker 解决 Splunk UBA SSO SAML 登入
cap理论、base 定理、分布式事务的理解与相互关系
flink1.15 异步维表Join 用于外部数据访问的异步 I/O scala版本
Certificate verification failed: The certificate is NOT trusted
ThreadLocal巨坑!内存泄露只是小儿科
async-validator.js数据校验器
- 原文地址:https://blog.csdn.net/ZZ_zhenzhen/article/details/136356458