java算法第十八天 | ● 110.平衡二叉树 ● 257. 二叉树的所有路径 ● 404.左叶子之和

110.平衡二叉树

leetcode链接
思路：
使用后序遍历分别求左右子树的高度，若高度只差大于一，则返回-1，否则返回当前节点的最大高度。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isBalanced(TreeNode root) {
        return !(getHeight(root)==-1);
    }

    public int getHeight(TreeNode node){
        if(node==null) return 0;
        int left=getHeight(node.left);
        if(left==-1) return -1;
        int right=getHeight(node.right);
        if(right==-1) return -1;
        if(Math.abs(left-right)>1){
            return -1;
        }else{
            return Math.max(left,right)+1;
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

257. 二叉树的所有路径

leetcode链接
思路： 这是大家第一次接触到回溯的过程， 我在视频里重点讲解了 本题为什么要有回溯，已经回溯的过程。

如果对回溯 似懂非懂，没关系， 可以先有个印象。
视频链接

我们先使用递归的方式，来做前序遍历。要知道递归和回溯就是一家的，本题也需要回溯。

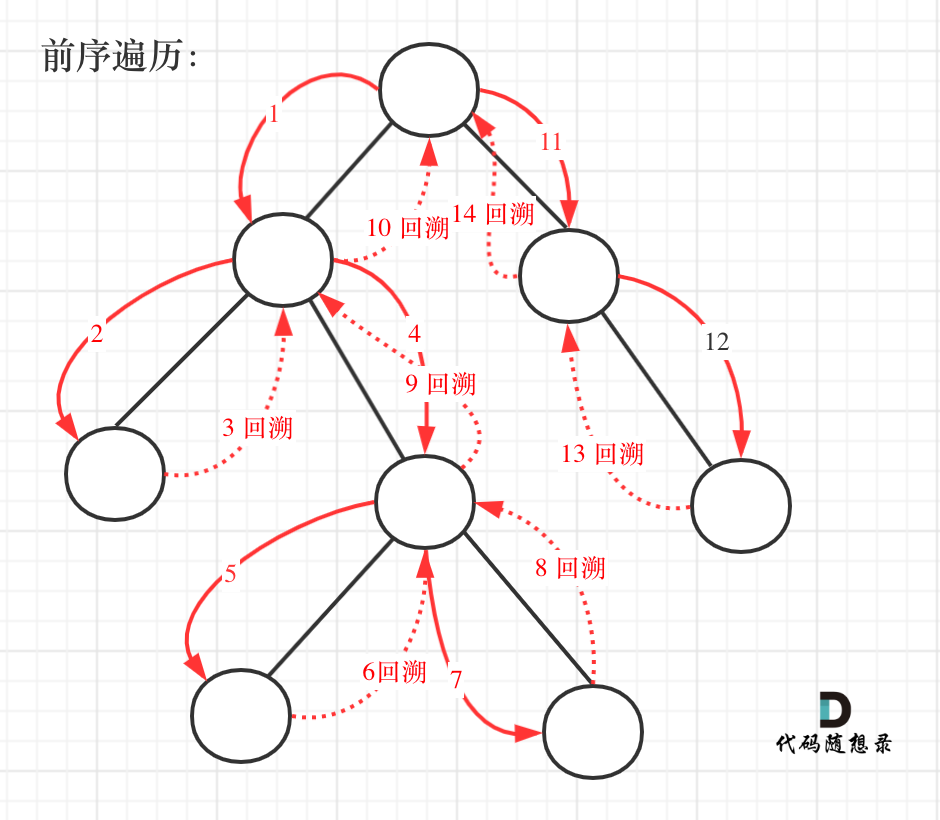
具体的教程可以看代码随想录的分析。

注意：

• 递归的传入参数设置和返回值。
• 递归出口中对结果的处理逻辑
• 回溯和调用递归函数应该是一一对应的，不能分开。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<String> binaryTreePaths(TreeNode root) {
        
        List<String> res=new ArrayList<>();
        List<Integer> path=new ArrayList<>();
        if(root==null) return res; 
        getResult(root,path,res);
        return res;


    }
    public void getResult(TreeNode node,List<Integer> path,List<String> res){
        path.add(node.val);
        if(node.left==null && node.right==null) {
            StringBuilder sb=new StringBuilder();
            for(int i=0;i<path.size()-1;i++){
                sb.append(path.get(i));
                sb.append("->");
            }
            sb.append(path.get(path.size()-1));
            res.add(sb.toString());
        }
        if(node.left!=null){
            getResult(node.left,path,res);
            path.remove(path.size()-1);
        }
        if(node.right!=null){
            getResult(node.right,path,res);
            path.remove(path.size()-1);
        }
    }

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

404.左叶子之和

leetcode链接
思路：
本题的重点是怎么判断左叶子节点。
判断当前节点是不是左叶子是无法判断的，必须要通过节点的父节点来判断其左孩子是不是左叶子。
依然使用递归法实现。
注意： 返回的是当前节点的左叶子之和，因此当遍历的叶子节点时返回的是0而不是叶子节点的val。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        return getLeftSum(root);
    }

    public int getLeftSum(TreeNode node){
        if(node==null) return 0;
        if(node.left==null && node.right==null) return 0;//注意
        int left=getLeftSum(node.left);
        if(node.left!=null && node.left.left==null && node.left.right==null) left=node.left.val;//注意这一行的位置
        int right=getLeftSum(node.right);
        return left+right;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29