极限学习机

极限学习机（ELM, Extreme Learning Machines）是一种前馈神经网络，ELM 不需要基于梯度的反向传播来调整权重，而是通过 Moore-Penrose generalized inverse来设置权值。

标准的单隐藏层神经网络结构如下：

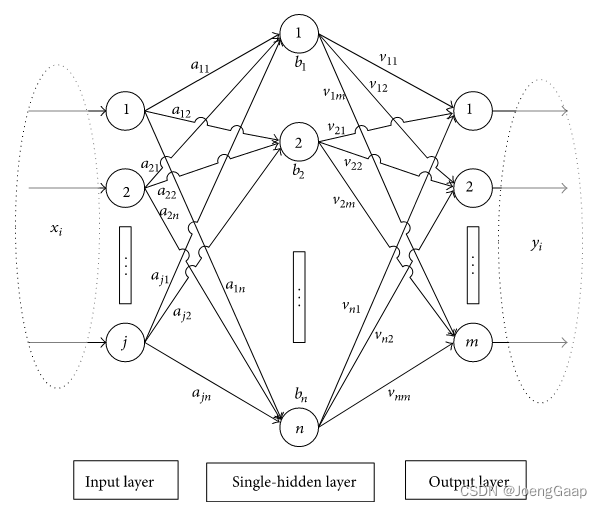
单隐藏层神经网络 | ELM网络

1. 输入值乘以权重值 | 输入值乘以权重值
2. 加上偏置值 | 加上偏置值
3. 进行激活函数计算 | 进行激活函数计算
4. 对每一层重复步骤1~3 | ×
5. 计算输出值 | 计算输出值
6. 误差反向传播 | 矩阵逆运算
7. 重复步骤1~6 | ×

极限学习机就是没有反向传播的简单神经网络，反向传播部分使用矩阵逆运算计算权重。

极限学习机前向传播：

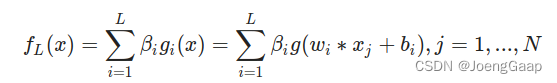
L 是隐藏单元的数量；N 是训练样本的数量；
beta 是第 i 个隐藏层和输出之间的权重向量（相当于图中的v）；w 是输入和隐藏层之间的权重向量(相当于图中的a)；
g 是激活函数；b 是偏置向量；x 是输入向量

可将这个函数看成：


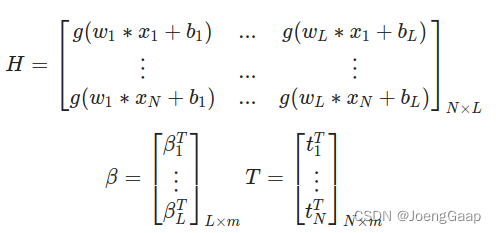
m 是输出的数量；
H 是隐藏层输出矩阵；
T 是训练集目标矩阵；

H是可逆的，T是已知的（因为它是已知标签结果）
||Hβ’-T||=min||Hβ-T||=0，即β’=H^-1T.。
所以这里需要求解的就是β的值。

ELM 算法主要过程:

1. wi,bi,i=1,L 随机初始化
2. 计算隐藏层输出
3. H 计算输出权重矩阵

极限学习机 Extreme Learning Machines 介绍

python代码实现

class RELM_HiddenLayer:
    """
        正则化的极限学习机
        :param x: 初始化学习机时的训练集属性X
        :param num: 学习机隐层节点数
        :param C: 正则化系数的倒数
    """

    def __init__(self, x, num, C=10):
        row = x.shape[0]
        columns = x.shape[1]
        rnd = np.random.RandomState()
        # 权重w
        self.w = rnd.uniform(-1, 1, (columns, num))
        # 偏置b
        self.b = np.zeros([row, num], dtype=float)
        for i in range(num):
            rand_b = rnd.uniform(-0.4, 0.4)
            for j in range(row):
                self.b[j, i] = rand_b
        self.H0 = np.matrix(self.softplus(np.dot(x, self.w) + self.b))
        self.C = C
        self.P = (self.H0.H * self.H0 + len(x) / self.C).I
        # .T:转置矩阵,.H:共轭转置,.I:逆矩阵

    @staticmethod
    def sigmoid(x):
        """
            激活函数sigmoid
            :param x: 训练集中的X
            :return: 激活值
        """
        return 1.0 / (1 + np.exp(-x))

    @staticmethod
    def softplus(x):
        """
            激活函数 softplus
            :param x: 训练集中的X
            :return: 激活值
        """
        return np.log(1 + np.exp(x))

    @staticmethod
    def tanh(x):
        """
            激活函数tanh
            :param x: 训练集中的X
            :return: 激活值
        """
        return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))

    # 分类问题 训练
    def classifisor_train(self, T):
        """
            初始化了学习机后需要传入对应标签T
            :param T: 对应属性X的标签T
            :return: 隐层输出权值beta
        """
        if len(T.shape) > 1:
            pass
        else:
            self.en_one = OneHotEncoder()
            T = self.en_one.fit_transform(T.reshape(-1, 1)).toarray()
            pass
        all_m = np.dot(self.P, self.H0.H)
        self.beta = np.dot(all_m, T)
        return self.beta

    # 分类问题 测试
    def classifisor_test(self, test_x):
        """
            传入待预测的属性X并进行预测获得预测值
            :param test_x:被预测标签的属性X
            :return: 被预测标签的预测值T
        """
        b_row = test_x.shape[0]
        h = self.softplus(np.dot(test_x, self.w) + self.b[:b_row, :])
        result = np.dot(h, self.beta)
        result = np.argmax(result, axis=1)
        return result
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81

基于python的ELM（极限学习机）分类及回归实现（附带自己数据链接及推导）