二分查找——34. 在排序数组中查找元素的第一个和最后一个位置

文章目录

• • 1. 题目
  • 2. 算法原理
  • • 2.1 暴力解法
    • 2.2 二分查找
    • • 左端点查找
      • 右端点查找
  • 3. 代码实现
  • 4. 二分模板

1. 题目

题目链接：34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣（LeetCode）

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]
1
2

示例 2：

输入：nums = [5,7,7,8,8,10], target = 6
输出：[-1,-1]
1
2

示例 3：

输入：nums = [], target = 0
输出：[-1,-1]
1
2

提示：

• 0 <= nums.length <= 105
• -109 <= nums[i] <= 109
• nums 是一个非递减数组
• -109 <= target <= 109

2. 算法原理

2.1 暴力解法

这里暴力解法也比较简单，直接遍历整个数组，记录第一次出现的位置和最后一次出现的位置，时间复杂度为O(N)，这里就不示例了。

2.2 二分查找

这里是不能够直接二分的，直接二分我们还需要从中间再往两边搜索，如果该数组里面的值全是目标值，效率就会降为O(N)。

这里还是利用二段性，我们可分开查找左右端点，分两种情况即可：

左端点查找

这里我们的判断条件是：nums[midi] < target和nums[midi] >= target

当midi落在左区间的的时候，肯定是没有我们要寻找的值的，我们让left = midi+1即可

当midi落在右区间的时候，这个区域里面是有可能有我们的target，不能让right = midi - 1，这样会导致错失我们的target，所以直接让right = midi即可

细节处理

• 循环条件：left < right
  这里一共就三种情况有目标值、全是大于目标值、全是小于目标值

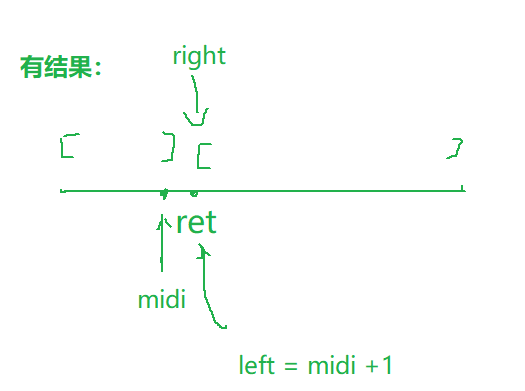
  1. 有结果：left一直在不符合条件的区间移动；right一直在符合条件的区间移动，且不会超出这个区间

     letf要执行，每次都是执行的midi+1，所以当left跳出去的时候，正好是在目标值处

     所以left == right时，就是最终结果，无需判断
     

  2. 全是大于target：在次情况下，左区间的条件一直都不会命中，而right，则一直在向left这边移动，最后相遇的时候，我们只需判断相遇处是不是target

  3. 全是小于target：这个情况就和上面这个一样

  如果我们在left == right的时候判断了，那么就会进入死循环，无限命中右区间条件

• 求中点：midi = left + (right - left)/2
  我们求中点的时候采用left+(right-left)/2这里是防止溢出，这种与left+(right-left+1)/2的区别就是当数组为偶数的时候，前者求的是靠左位置，而后者是靠右位置
  

  这个在普通二分是没什么影响的，可是在我们求端点的时候，进行最后一次操作：
  

  采用②求中点时，命中右区间的条件，则会陷入死循环

右端点查找

查找右端点和查找左端点思想一致

这个求中点的方式就采用left+(right-left+1)/2靠右位置

3. 代码实现

class Solution
{
public:
    vector<int> searchRange(vector<int>& nums, int target)
    {
        //检查空数组
        if(nums.size() == 0)    return {-1,-1};

        int left = 0;
        int right = nums.size()-1;
        int begin = left;
        //查找左端点
        while(left < right)
        {
            int midi = left+(right-left)/2;
            if(nums[midi]<target)
            {
                left = midi+1;
            }
            else    right = midi;
        }
        //判断是否有结果
        if(nums[left] != target)    return {-1,-1};
        else    begin = left;   //记录左端点

        //查找右端点
        //left = 0;   //可不用重置
        right = nums.size()-1;
        while(left<right)
        {
            int midi = left+(right-left+1)/2;
            if(nums[midi]<=target)
            {
                left = midi;
            }
            else    right = midi-1;
        }
        return {begin,right};
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

4. 二分模板

查找区间左端点：

while(left<right)
{
    int mid = left + (right -left)/2;
    if(...)
    {
        left = mid + 1；
    }
    else
    {
        right = mid;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12

查找区间右端点：

while(left<right)
{
    int mid = left + (right -left+1)/2;
    if(...)
    {
        left = mid；
    }
    else
    {
        right = mid - 1;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12

当下面出现减肥的时候，上面就用加一