[acwing周赛复盘] 第 94 场周赛20230311

总结

• 好久没做acw了，挺难的。
• T1 模拟
• T2 前缀和以及优化。
• T3 贪心
• 

5295. 三元组

链接: 5295. 三元组

1. 题目描述

2. 思路分析

• 设a=sum(0,x),b=sum(y,z)。那么best=a+b-(s-a-b)=2(a+b)-s。
• 那么其实是找最大的a+b。用前缀和来处理这个事情。
• 即pre[x] + (pre[z] - pre[y]),注意其实可以用左闭右开写法。
• 由于数据量5000，可以枚举y和z，记录y之前的最大x即可。

---

• 也可以优化成O(n),有点类似状态机DP。

3. 代码实现

def solve():
    """
    best = (0~x)+(y~z) - (s-(0~x)-(y~z)) = 2((0~x)+(y~z)) - s
    因此是 找最大的两段和， pre[x] + pre[z] - pre[y],其中x<=y<=z,
    记录y之前最大的pre[x]，z之前最大的pre[x]-pre[y]即可
    """
    n, = RI()
    a = RILST()
    p = 0
    mx = [0, 0, 0, 0]  # best,x,y,z
    px = [0, 0]  # prex,x
    py = [0, 0, 0]  # pre[x]-pre[y]
    for z, v in enumerate(a, start=1):
        p += v
        px = max(px, [p, z])
        py = max(py, [px[0] - p, px[1], z])
        mx = max(mx, [p + py[0], py[1], py[2], z])       
    print(*mx[1:])


def solve1():
    n, = RI()
    a = RILST()
    pre = [0] + list(accumulate(a))
    mx = [0, 0, 0, 0]
    pm = [(i, v) for i, v in enumerate(pre)]
    for i in range(1, n + 1):
        if pm[i][1] <= pm[i - 1][1]:
            pm[i] = pm[i - 1][:]
    for y in range(0, n):
        for z in range(y, n):
            mx = max(mx, [pre[z + 1] - pre[y] + pm[y][1], pm[y][0], y, z + 1])
    print(*mx[1:])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

5296. 边的定向

链接: 5296. 边的定向

1. 题目描述

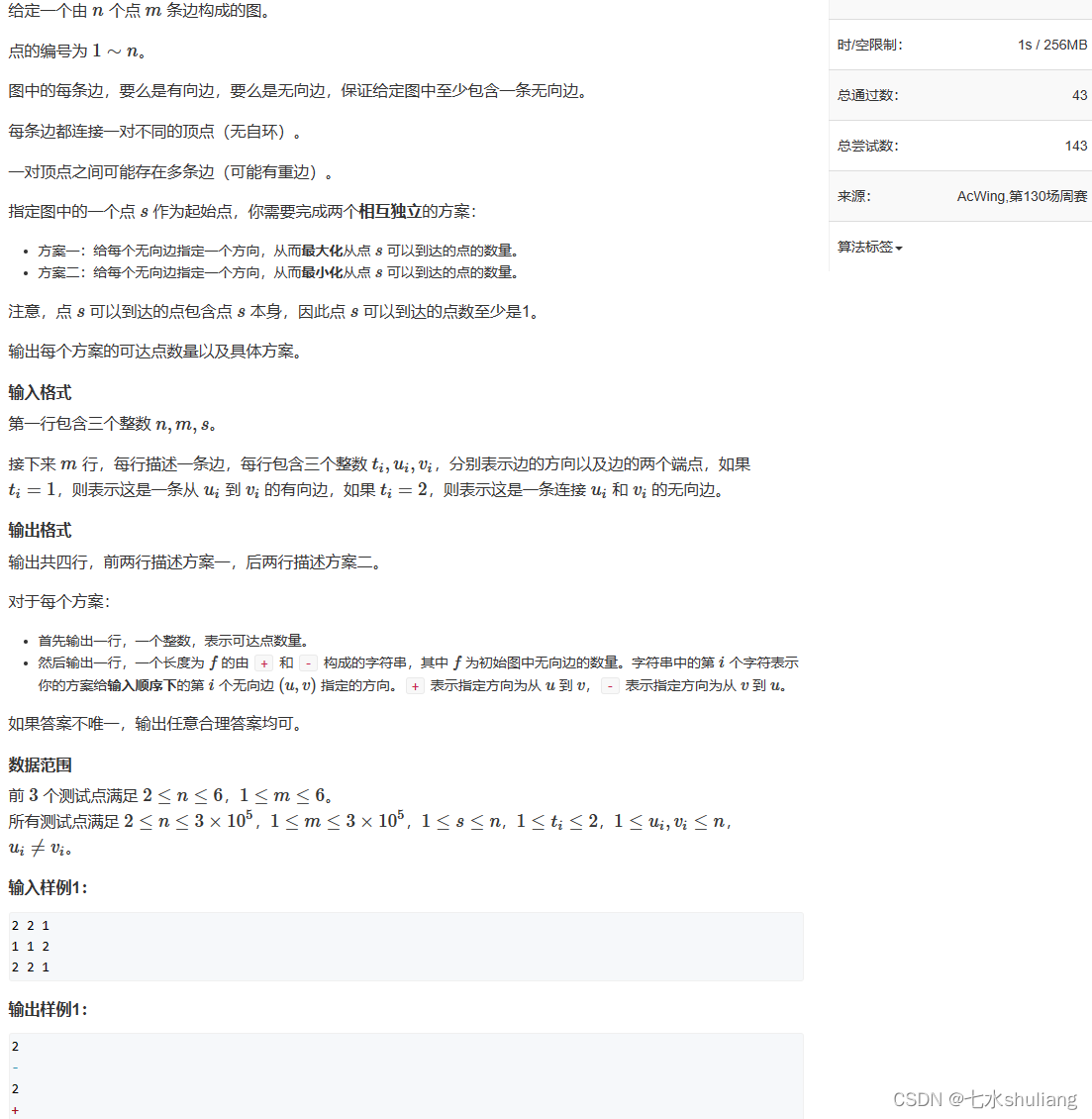
2. 思路分析

貌似很难，但其实贪心能过。
1

• 最大访问数就是尽量向外延伸，把所有访问到的边都朝外指。
• 最小访问数就是遇到的边超里指，只走本来就有的有向边。
• 代码实现时，建图记录边的id，遇到时判断当前方向和输入方向是否一致决定方向。
• 注意有的边可能不会遇到，可以是任意方向。

3. 代码实现

def solve():
    n, m, s = RI()
    g = [[] for _ in range(n + 1)]
    edges = []
    for i in range(m):
        t, u, v = RI()
        edges.append((u, v, t))
        g[u].append((v, i))
        if t == 2:
            g[v].append((u, i))

    q = deque([s])  # 把遇到的边都变成正向
    vis = {s}
    d = [0] * m
    while q:
        u = q.popleft()
        for v, i in g[u]:
            if v not in vis:
                vis.add(v)
                q.append(v)
                if edges[i][2] == 2:  # 如果是无向边，让他u->v
                    d[i] = '+' if u == edges[i][0] else '-'
    print(len(vis))
    ans = []
    for x, (_, _, t) in zip(d, edges):
        if t == 2:
            ans.append(x if x else '+')
    print(''.join(ans))

    q = deque([s])  # 把遇到的边都变成负向
    vis = {s}
    d = [0] * m
    while q:
        u = q.popleft()
        for v, i in g[u]:
            if v not in vis:
                if edges[i][2] == 1:  # 有向边必须走
                    vis.add(v)
                    q.append(v)
                else:  # 无向边不走，u<-v
                    d[i] = '-' if u == edges[i][0] else '+'
    print(len(vis))
    ans = []
    for x, (_, _, t) in zip(d, edges):
        if t == 2:
            ans.append(x if x else '+')
    print(''.join(ans))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

六、参考链接

• 无