-
无线物理层安全大作业

Beamforming Optimization for Physical Layer Security in MISO Wireless Networks
2018 TSP
考虑由窃听者窃听的多个发射机-用户对组成的无线网络,其中发射机配备有多个天线,而用户和窃听者配备有单个天线。在不同级别的无线信道知识中,感兴趣的问题是波束成形,以根据用户的保密吞吐量优化用户的服务质量(QoS),或在用户的 QoS 下最大化网络的能源效率。所有这些问题都被视为非常困难的优化问题,在波束成形向量中具有许多非凸约束和非线性等式约束。本文开发了低复杂度和快速收敛的路径跟踪计算程序,以获得最佳波束形成解决方案。通过数值例子证明了它们的实用性。保护信息已成为无线通信中最关键的问题之一[1]、[2]。无线传输的广播性质意味着它们很容易受到对手的攻击,对手试图拦截其信息传递或无意中听到为其用户提供的机密信息[3]、[4]。已经提出利用无线信道[5]、[6]的物理特性的物理层安全性(PLS)来确保向低复杂性的最终用户传输数据的保密性,对此不能使用加密。 PLS 基于保密的信息论特征,窃听者 (EV) 监听到的无线传输的用户保密吞吐量被确定为用户吞吐量与 EV 吞吐量之间的差值 [2]、[7]。传输波束成形可提高用户吞吐量,同时控制 EV 处窃听信号的吞吐量,从而提供了一种增强保密吞吐量的有效方法。 [8]-[12] 中已经考虑通过半定松弛和随机化以及已知的低效率 [13] 来最大化瞬时保密吞吐量的波束成形设计。这种波束成形设计已在[14]、[15]中成功解决。关于中断概率,[16]-[19]等一些著作使用了未发表的著作[20]中获得的伯恩斯坦型不等式。我们将证明,基于这种伯恩斯坦型不等式的结果可能非常保守。参考文献[21]考虑了在不完美信道状态信息(CSI)下给定波束形成器的中断区域特征。
另一方面,随着能源效率(EE)成为无线通信中非常严重的问题[22]、[23],安全能源效率(SEE),即保密吞吐量与总网络功耗的比率,以每焦耳每赫兹的保密位数来衡量在 PLS 中也越来越重要 [24]、[25]。利用完美的CSI,[26]-[28]中的SEE最大化基于昂贵的波束形成器,它完全消除了EV上的多用户干扰和窃听信号。 [29]和[30]中单用户多输入多输出(MIMO)/单输入单输出(SISO)通信的SEE优化算法的计算复杂度也很高,因为每次迭代仍然涉及困难非凸优化问题。我们之前的工作 [31] 考虑了更一般的 MIMO 网络情况的 SEE 优化。 [15] 中还考虑了 SEE 优化,以应对用户和电动汽车渠道不确定性的最坏情况。目前还没有关于在中断概率方面具有保密吞吐量的 SEE 优化的现有工作。
在本文中,我们考虑由窃听者 (EV) 窃听的多个发射器用户对组成的网络。由于假设发射机配备多个天线,而用户和 EV 配备单个天线,因此目标是设计发射波束形成器,以在保密吞吐量方面优化用户的服务质量 (QoS)或用户QoS下网络的SEE。应该意识到,波束成形设计的这些问题仍然有广泛的研究空间,因此我们在不同的信道知识层面上考虑它们。本文的结构如下。第二节专门讨论问题陈述。第三部分考虑了所有相关通道的完美 CSI 下的这些问题,其中开发了低复杂度的路径跟踪算法来解决这些问题。在第四节中,假设发射机和用户之间的信道的完美CSI,但仅假设发射机和EV之间的信道分布是已知的。因此,EV 的吞吐量不是确定性定义的,而是通过其中断概率来定义的,这导致波束成形向量和 EV 吞吐量中的非线性方程,使得波束成形设计在计算上更具挑战性。在与第四节中发射机和EV之间的信道相同的知识下,第五节还假设发射机和用户之间的信道是不确定的,具有高斯分布误差,在这种情况下,用户的中断概率没有已知的结果。吞吐量。尽管如此,基于附录一中获得的新的中断概率结果,用户的QoS优化和网络的SEE优化问题都得到了成功的解决。第五节的仿真显示了第三节至第五节中开发的路径跟踪算法的效率。第六节给出了结论。附录一提供了有关中断感知用户吞吐量上限和下限的新结果。附录二显示了其他一些结果的保守性,这些结果基于伯恩斯坦型不等式。附录 III 中给出了第 III-V 节中使用的一些基本确定性不等式。
Problem Stateme
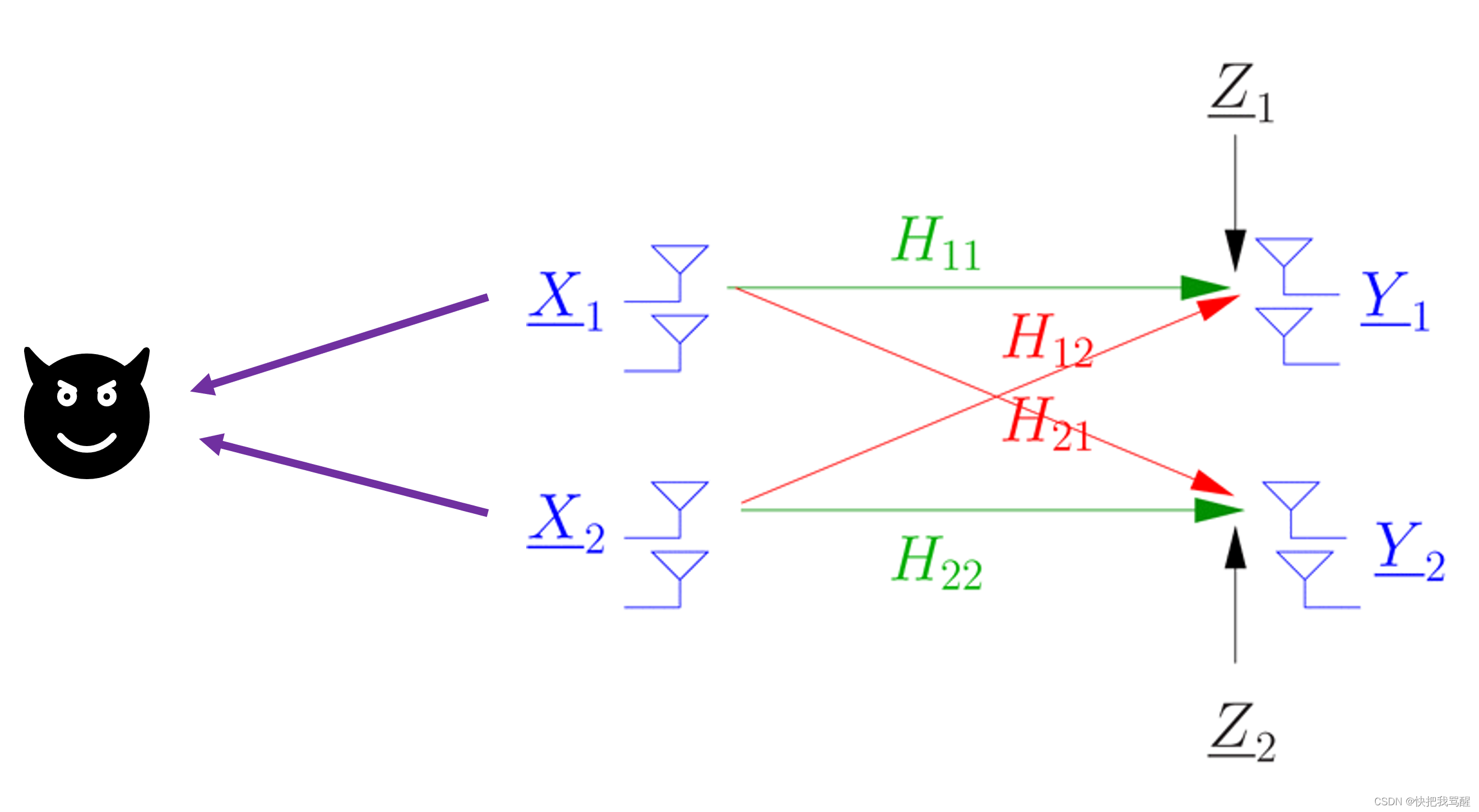
考虑由 EV 监听的 M 个发射机-用户对的通信网络。每个发射机配备Nt个发射天线,而用户和EV配备单个天线。因此,在没有 EV 的情况下,网络看起来非常类似于[32]-[36]中考虑的网络,其中信道知识是从信道估计中获得的,信道估计在网络的中央处理单元中实现,而波束成形在网络的信号处理块。用户 i i i 的信息 s i s_i si 被归一化为 E ( s i 2 ) = 1 E(s^2_i )=1 E(si2)=1,通过 w i ∈ C N t \mathbf{w}_i \in \mathbb{C}^{N_t} wi∈CNt 进行波束形成。用户 i i i处接收到的信号为
y i = h i i H w i s i + ∑ j ≠ i M h j i H w j s j + n i (1) y_{i}=h_{i i}^{H} \mathbf{w}_{i} s_{i}+\sum_{j \neq i}^{M} h_{j i}^{H} \mathbf{w}_{j} s_{j}+n_{i} \tag{1} yi=hiiHwisi+j=i∑MhjiHwjsj+ni(1)
-
相关阅读:
都2023年金九银十了,这三个项目你还没有?你简历上项目经验写啥
Blazor前后端框架Known-V1.2.11
大坑-MATLAB图片转存时需注意的点
Navicat15工具连接PostgreSQL15失败
【CSDN创作活动】 - 我参加过的那些竞赛
Springboot整合logback多节点日志文件加端口号区分
Java前后端分离的在线考试系统源码
递归代码和动态规划代码相互转化
【1024程序员节】代码写诗(C++版)
Qt读取Json文件(含源码+注释)
- 原文地址:https://blog.csdn.net/qq_45542321/article/details/134461148