代码随想录算法训练营第22天|235. 二叉搜索树的最近公共祖先 701. 二叉搜索树中的插入操作 450.删除二叉搜索树中的节点

JAVA代码编写

235. 二叉搜索树的最近公共祖先

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

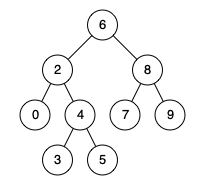
示例 1:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6 
解释: 节点 2 和节点 8 的最近公共祖先是 6。
1
2
3

示例 2:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
1
2
3

说明:

• 所有节点的值都是唯一的。
• p、q 为不同节点且均存在于给定的二叉搜索树中。

教程：https://programmercarl.com/0235.%E4%BA%8C%E5%8F%89%E6%90%9C%E7%B4%A2%E6%A0%91%E7%9A%84%E6%9C%80%E8%BF%91%E5%85%AC%E5%85%B1%E7%A5%96%E5%85%88.html

视频：https://www.bilibili.com/video/BV1jd4y1B7E2

方法一：递归

思路：根结点的值都大于p和q的值，就继续在左子树中递归，否则就右子树中继续递归。

复杂度分析：

• 时间复杂度: O(n)，其中n是二叉树中节点的个数
• 空间复杂度:
  • 在递归调用的过程中，在最坏情况下是O(n)
  • 在平衡的二叉搜索树中，递归的层数通常为log(n)

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode() {}
    TreeNode(int val) { this.val = val; }
    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if (root.val > p.val && root.val > q.val) return lowestCommonAncestor(root.left, p, q);
        if (root.val < p.val && root.val < q.val) return lowestCommonAncestor(root.right, p, q);
        return root;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

701. 二叉搜索树中的插入操作

给定二叉搜索树（BST）的根节点 root 和要插入树中的值 value ，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ，新值和原始二叉搜索树中的任意节点值都不同。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。

示例 1：

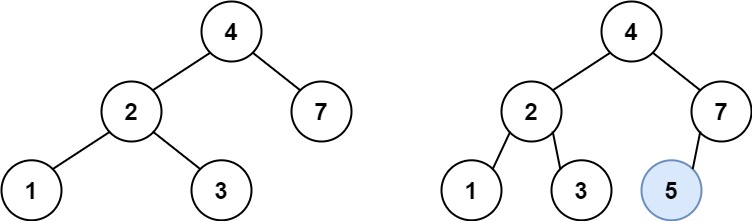
输入：root = [4,2,7,1,3], val = 5
输出：[4,2,7,1,3,5]
解释：另一个满足题目要求可以通过的树是：
1
2
3

示例 2：

输入：root = [40,20,60,10,30,50,70], val = 25
输出：[40,20,60,10,30,50,70,null,null,25]
1
2

示例 3：

输入：root = [4,2,7,1,3,null,null,null,null,null,null], val = 5
输出：[4,2,7,1,3,5]
1
2

提示：

• 树中的节点数将在 [0, 104]的范围内。
• -108 <= Node.val <= 108
• 所有值 Node.val 是 独一无二 的。
• -108 <= val <= 108
• 保证 val 在原始BST中不存在。

教程：https://programmercarl.com/0701.%E4%BA%8C%E5%8F%89%E6%90%9C%E7%B4%A2%E6%A0%91%E4%B8%AD%E7%9A%84%E6%8F%92%E5%85%A5%E6%93%8D%E4%BD%9C.html#%E7%AE%97%E6%B3%95%E5%85%AC%E5%BC%80%E8%AF%BE

视频：https://www.bilibili.com/video/BV1Et4y1c78Y/

方法一：递归

思路：

复杂度分析：

• 时间复杂度: O(h)，其中h是二叉搜索树的高度，最坏情况下为O(n)，其中n是树中节点的数量。
• 空间复杂度: O(1)

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode() {}
    TreeNode(int val) { this.val = val; }
    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

class Solution {
    public TreeNode insertIntoBST(TreeNode root, int val) {
        if (root == null) return new TreeNode(val);
        TreeNode newRoot = root;
        TreeNode pre = root;
        while (root != null) {
            pre = root;
            if (root.val > val) {
                root = root.left;
            } else if (root.val < val) {
                root = root.right;
            } 
        }
        if (pre.val > val) {
            pre.left = new TreeNode(val);
        } else {
            pre.right = new TreeNode(val);
        }

        return newRoot;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

450. 删除二叉搜索树中的节点

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

1. 首先找到需要删除的节点；
2. 如果找到了，删除它。

示例 1:

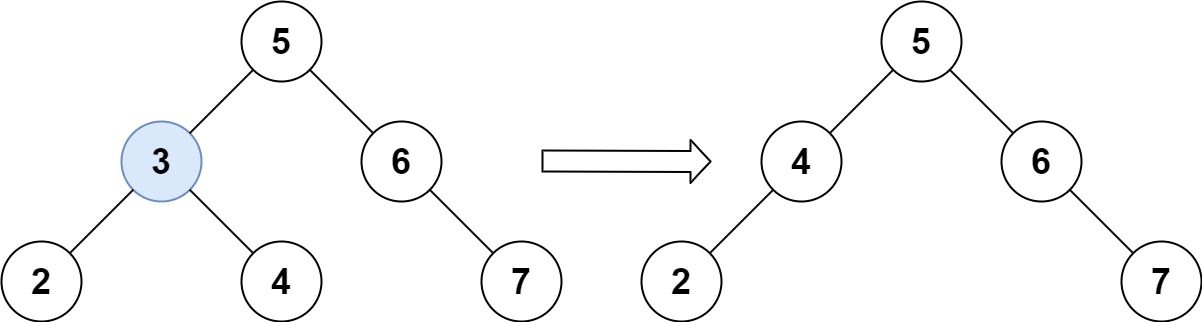
输入：root = [5,3,6,2,4,null,7], key = 3
输出：[5,4,6,2,null,null,7]
解释：给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。
1
2
3
4
5

示例 2:

输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点
1
2
3

示例 3:

输入: root = [], key = 0
输出: []
1
2

提示:

• 节点数的范围 [0, 104].
• -105 <= Node.val <= 105
• 节点值唯一
• root 是合法的二叉搜索树
• -105 <= key <= 105

进阶： 要求算法时间复杂度为 O(h)，h 为树的高度。

教程：https://programmercarl.com/0450.%E5%88%A0%E9%99%A4%E4%BA%8C%E5%8F%89%E6%90%9C%E7%B4%A2%E6%A0%91%E4%B8%AD%E7%9A%84%E8%8A%82%E7%82%B9.html

视频：https://www.bilibili.com/video/BV1tP41177us/

方法一：递归

思路：

复杂度分析：

• 时间复杂度: O(h)，其中h是二叉搜索树的高度，最坏情况是O(n)
• 空间复杂度: O(n)，n是树的节点数量

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode() {}
    TreeNode(int val) { this.val = val; }
    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

class Solution {
  public TreeNode deleteNode(TreeNode root, int key) {
    if (root == null) return root;
    if (root.val == key) {
      if (root.left == null) {
        return root.right;
      } else if (root.right == null) {
        return root.left;
      } else {
        TreeNode cur = root.right;
        while (cur.left != null) {
          cur = cur.left;
        }
        cur.left = root.left;
        root = root.right;
        return root;
      }
    }
    if (root.val > key) root.left = deleteNode(root.left, key);
    if (root.val < key) root.right = deleteNode(root.right, key);
    return root;
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36