01序列 卡特兰数

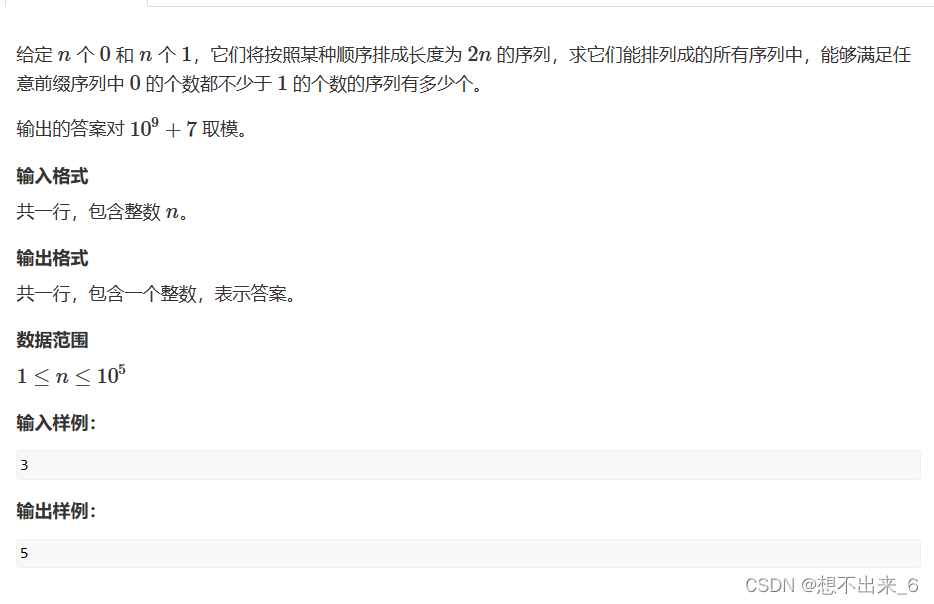
 解法：

将01序列置于坐标轴上，起始点为原点。0表示向右走，1表示向上走。这样就可以将前缀0的个数不少于1的个数就可以转换为路径上的点，横坐标大于纵坐标，也就是求合法路径个数。

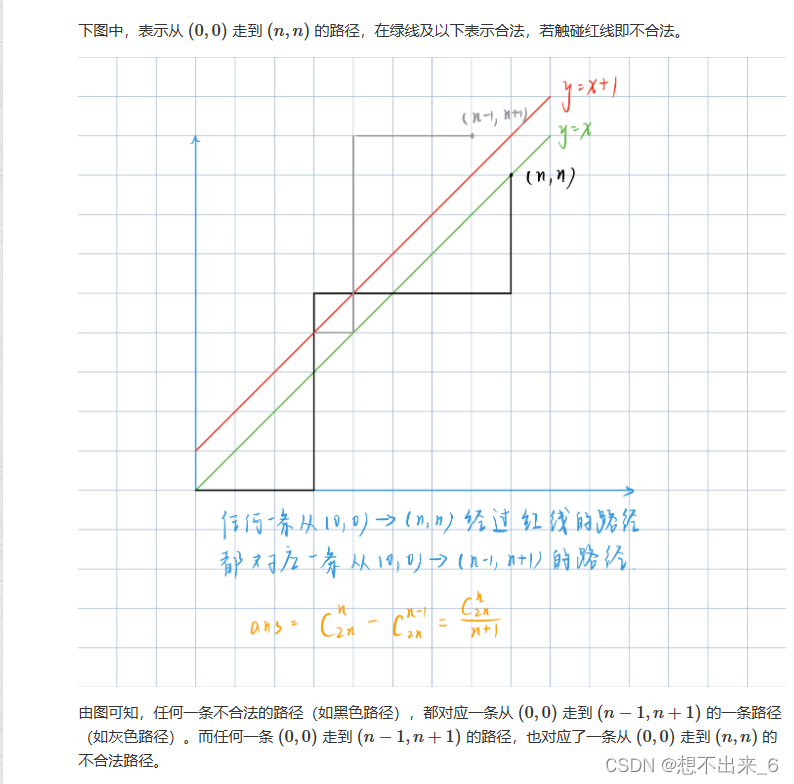
注意题目mod的数是质数，所以可以使用快速幂求逆元，若不是质数，则需要使用扩展欧几里得算法求逆元。 

快速幂：

//01序列 卡特兰数
#include
using namespace std;
using ll = long long;
const ll mod = 1e9 + 7;
 
//因为mod的数是质数可以用快速幂
//如果不是质数就用扩展欧几里得
ll qmi(ll a, ll k, ll p)
{
	ll res = 1;
 
	while (k)
	{
		if (k & 1) res = res * a % p;
		a = a * a % p;
		k >>= 1;
	}
	return res;
}
//答案为C2n n /n + 1
int main()
{
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	ll n; cin >> n;
 
	ll a = 2 * n, b = n, res = 1;
 
	for (ll i = a; i > a - b; --i) res = res * i % mod;
	for (ll i = 1; i <= b; ++i) res = res * qmi(i, mod - 2, mod) % mod;
 
	res = res * qmi(n + 1, mod - 2, mod) % mod;
	cout << res;
	return 0;
}

扩展欧几里得：

//01序列 扩展欧几里得
#include
using namespace std;
using ll = long long;
const ll mod = 1e9 + 7;
 
ll exgcd(ll a, ll b, ll& x, ll& y)
{
	if (!b)
	{
		x = 1, y = 0;
		return a;
	}
 
	ll d = exgcd(b, a % b, y, x);
	y -= a / b * x % mod;
	return d;
}
 
int main()
{
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
 
	ll n, x, y; cin >> n;
	ll a = 2 * n, b = n;
	ll res = 1;
 
	for (ll i = a; i > a - b; --i) res = res * i % mod;
	for (ll i = 1; i <= b; ++i)
	{
		exgcd(i, mod, x, y);
		res = res * x % mod;
	}
	exgcd(n + 1, mod, x, y);
	res = (res * x % mod + mod) % mod;
	cout << res;
	return 0;
}